辽宁省鞍山市五校2022-2023学年高二下学期期末考试数学试题(Word版含答案)
文档属性
| 名称 | 辽宁省鞍山市五校2022-2023学年高二下学期期末考试数学试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 530.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 00:00:00 | ||
图片预览




文档简介
鞍山市五校2022-2023学年高二下学期期末考试
数学试卷
一 单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知曲线在处的切线方程是,则与分别为( )
A. B. C. D.
2.“”是“”成等比数列的( )条件
A.充分不必要 B.必要不充分
C.充要 D.既不充分又不必要
3.已知,则( )
A. B. C. D.0
4.在辽宁电视台有一闯关节目,该节目设置有两关,闯关规则是:当第一关闯关成功后,方可进入第二关.为了调查闯关的难度,该电视台调查了参加过此节目的100名选手的闯关情况,第一关闯关成功的有70人,第一关闯关成功且第二关闯关也成功的选手有63人,以闯关成功的频率近似作为闯关成功的概率,已知某个选手第一关闯关成功,则该选手第二关闯关成功的概率为( )
A.0.63 B.0.7 C.0.9 D.0.431
5.已知指数曲线进行适当变换后得到的方程为,则二次函数的单调递增区间为( )
A. B. C. D.
6.已知正项数列的前项和为,且,则( )
A. B. C. D.
7.已知某疾病的某种疗法治愈率为.若有100位该病患者采取了这种疗法,且每位患者治急与否相互独立,设其中被治急的人数为,则下列选项中正确的是( )
A.
B.
C.
D.存在,使得成立
8.已知函数的图象恒在的图象的下方,则实数的取值范围是( )
A. B. C. D.
二 多选题(本大题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.下列命题正确的有( )
A.若等差数列的前项的和为,则成等差数列
B.若为等比数列,且,则
C.若等差数列的前项和为,已知,且,则的最大值是
D.若,则数列的前2024项和为4048
10.已知具有相关关系的两个变量的一组观测数据,由此得到的线性回归方程为,则下列说法中正确的是( )
A.回归直线至少经过点中的一个点
B.若,则回归直线一定经过点
C.若点都落在直线上,则变量的样本相关系数
D.若,则相应于样本点的残差为-3
11.若数列满足,则称数列为斐波那契数列,又称黄金分割数列.在现代物理 准晶体结构 化学等领域,斐波那契数列都有直接的应用.则下列结论成立的是( )
A.
B.
C.
D.
12.对于函数,下列说法正确的是( )
A.在上单调递增,在上单调递减
B.若方程有4个不等的实根,则
C.当时,
D.设,若对,使得成立,则
三 填空题(本大题共4小题,每小题5分,共20分)
13.函数的极值点为__________.
14.设某批产品中,甲 乙 丙三个车间生产的产品分别占,甲 丙车间生产的产品的次品率分别为和.现从中任取一件,若取到的是次品的概率为,则推测乙车间的次品率为__________.
15.在数列中,,且.则数列的通项公式为__________.
16.已知函数,若曲线与曲线存在公切线,则实数的最大值为__________.
四 解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)已知函数.
(1)若在处的切线与直线垂直,求实数的值;
(2)若,求函数的极值.
18.(本小题满分12分)绿水青山就是金山银山,沈阳环保部门随机调查了2022年,100天中每天的空气质量等级和当天到浑河绿道锻炼的人次,整理数据得到下表(单位天):
锻炼人次 空气质量等级
1(优) 6 10 25
2(良) 9 10 12
3(轻度污染) 7 8 7
4(中度污染) 3 2 1
若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.
(1)估计沈阳市2022年(365天)“空气质量好”的天数(结果四舍五入保留整数);
(2)根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有99%的把握认为一天中到浑河绿道锻炼的人次与沈阳市当天的空气质量有关?
人次 人次
空气质量好
空气质量不好
附:.
0.1 0.01 0.001
2.706 6.635 10.828
19.(本小题满分12分)已知数列中,.
(1)求证:数列是等比数列;
(2)若数列满足,求数列的前项和.
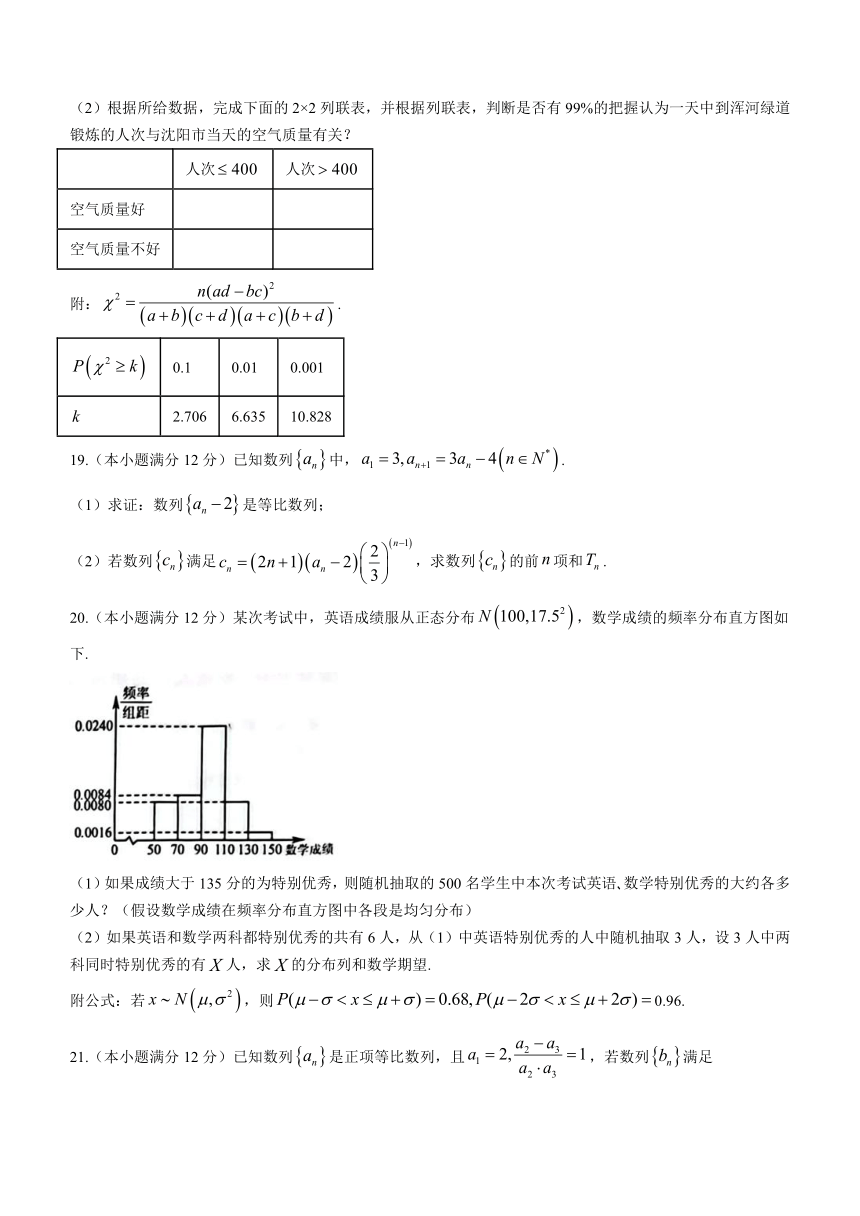
20.(本小题满分12分)某次考试中,英语成绩服从正态分布,数学成绩的频率分布直方图如下.
(1)如果成绩大于135分的为特别优秀,则随机抽取的500名学生中本次考试英语 数学特别优秀的大约各多少人?(假设数学成绩在频率分布直方图中各段是均匀分布)
(2)如果英语和数学两科都特别优秀的共有6人,从(1)中英语特别优秀的人中随机抽取3人,设3人中两科同时特别优秀的有人,求的分布列和数学期望.
附公式:若,则0.96.
21.(本小题满分12分)已知数列是正项等比数列,且,若数列满足.
(1)求数列和的通项公式;
(2)已知,记.若恒成立,求实数的取值范围.
22.(本小题满分12分)已知函数,其中.
(1)若,讨论函数的单调性;
(2)已知是函数的两个零点,且,证明:.
鞍山市五校2022-2023学年高二下学期期末考试
数学试卷参考答案与评分标准
一 单选题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1 2 3 4 5 6 7 8
D B D C C C B A
二 多选题(本大题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9 10 11 12
BCD BCD ABC BD
三 填空题(本大题共4小题,每小题5分,共20分)
13. 14. 15. 16.
四 解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题10分)
【解析】
(1)因为函数
所以,
因为在处的切线与直线垂直
由导数的几何意义及两条直线互相垂直条件可知,得
解得
(2)当时,,
当时,,当时,,
所以函数在区间上单调递减,在区间上单调递增,
所以当时,函数取得极小值1,无极大值.
18.(本小题12分)
【解折】
(1)依题意可得,该市一天的空气质量等级为1的概率为,
等级为2的概率为
所以“空气质量好”的概率为
所以2022年(365天)“空气质量好”的天数为(天)
因此估计沈阳市2022年(365天)“空气质显好”的天数为263天-
(2)依题意列联表如下所示:
人次 人次>400
空气质是好 35 37
空气质量不好 20 8
所以
因此没有的把握认为一天中到浑河绿道锻炼的人次与沈阳市当天的空气质量有关.
19.(本小题12分)
【解析】(1)因为,
所以,
所以,
所以数列是以1为首项,3为公比的等比数列
(2)由(1)知,因为,
所以
所以,,
两式相减,得,
所以
20.(本小遈12分)
【解析】(1),
,故英语成绩特别优秀的有人.
由频率分布直方图知,数学成绩特别优秀的频率为
故数学成绩待别优秀的有人.
(2)依题意:取值集合
其分布列为:
0 1 2 3
21.(本小题满分12分)
【解折】(1)设数列的公比为,则,
因为,由已知可得,所以,
即,解得(舍去)或,
故数列的通项公式为.
因为,所以,
又由,得,所以当时,
经检验,也满足上式,所以
(2)由(1)得,
所以
又恒成立,所以恒成立.
设
则.
易知当时,;当时,.
于是,
所以,
所以实数的取值范围是
22.(本小题满分12分)
【解析】(1)若,即,
可得,
①若,则,
即在单调递减:
②若,令有,令有
即在上单调递减,上单调递增,
综上可得:当在单调递减;
当在上单调递减,上单调递增.
(2)解:由题意知是的两个零点,且,
即,
所以,
即,
要证:,
只需证:
即证:,
即证:,令,
即证:令,
可得,
即在上单调递增,则,
即,
设,有,
所以在上单调递减,
则,即
综上可得:
数学试卷
一 单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知曲线在处的切线方程是,则与分别为( )
A. B. C. D.
2.“”是“”成等比数列的( )条件
A.充分不必要 B.必要不充分
C.充要 D.既不充分又不必要
3.已知,则( )
A. B. C. D.0
4.在辽宁电视台有一闯关节目,该节目设置有两关,闯关规则是:当第一关闯关成功后,方可进入第二关.为了调查闯关的难度,该电视台调查了参加过此节目的100名选手的闯关情况,第一关闯关成功的有70人,第一关闯关成功且第二关闯关也成功的选手有63人,以闯关成功的频率近似作为闯关成功的概率,已知某个选手第一关闯关成功,则该选手第二关闯关成功的概率为( )
A.0.63 B.0.7 C.0.9 D.0.431
5.已知指数曲线进行适当变换后得到的方程为,则二次函数的单调递增区间为( )
A. B. C. D.
6.已知正项数列的前项和为,且,则( )
A. B. C. D.
7.已知某疾病的某种疗法治愈率为.若有100位该病患者采取了这种疗法,且每位患者治急与否相互独立,设其中被治急的人数为,则下列选项中正确的是( )
A.
B.
C.
D.存在,使得成立
8.已知函数的图象恒在的图象的下方,则实数的取值范围是( )
A. B. C. D.
二 多选题(本大题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.下列命题正确的有( )
A.若等差数列的前项的和为,则成等差数列
B.若为等比数列,且,则
C.若等差数列的前项和为,已知,且,则的最大值是
D.若,则数列的前2024项和为4048
10.已知具有相关关系的两个变量的一组观测数据,由此得到的线性回归方程为,则下列说法中正确的是( )
A.回归直线至少经过点中的一个点
B.若,则回归直线一定经过点
C.若点都落在直线上,则变量的样本相关系数
D.若,则相应于样本点的残差为-3
11.若数列满足,则称数列为斐波那契数列,又称黄金分割数列.在现代物理 准晶体结构 化学等领域,斐波那契数列都有直接的应用.则下列结论成立的是( )
A.
B.
C.
D.
12.对于函数,下列说法正确的是( )
A.在上单调递增,在上单调递减
B.若方程有4个不等的实根,则
C.当时,
D.设,若对,使得成立,则
三 填空题(本大题共4小题,每小题5分,共20分)
13.函数的极值点为__________.
14.设某批产品中,甲 乙 丙三个车间生产的产品分别占,甲 丙车间生产的产品的次品率分别为和.现从中任取一件,若取到的是次品的概率为,则推测乙车间的次品率为__________.
15.在数列中,,且.则数列的通项公式为__________.
16.已知函数,若曲线与曲线存在公切线,则实数的最大值为__________.
四 解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)已知函数.
(1)若在处的切线与直线垂直,求实数的值;
(2)若,求函数的极值.
18.(本小题满分12分)绿水青山就是金山银山,沈阳环保部门随机调查了2022年,100天中每天的空气质量等级和当天到浑河绿道锻炼的人次,整理数据得到下表(单位天):
锻炼人次 空气质量等级
1(优) 6 10 25
2(良) 9 10 12
3(轻度污染) 7 8 7
4(中度污染) 3 2 1
若某天的空气质量等级为1或2,则称这天“空气质量好”;若某天的空气质量等级为3或4,则称这天“空气质量不好”.
(1)估计沈阳市2022年(365天)“空气质量好”的天数(结果四舍五入保留整数);
(2)根据所给数据,完成下面的2×2列联表,并根据列联表,判断是否有99%的把握认为一天中到浑河绿道锻炼的人次与沈阳市当天的空气质量有关?
人次 人次
空气质量好
空气质量不好
附:.
0.1 0.01 0.001
2.706 6.635 10.828
19.(本小题满分12分)已知数列中,.
(1)求证:数列是等比数列;
(2)若数列满足,求数列的前项和.
20.(本小题满分12分)某次考试中,英语成绩服从正态分布,数学成绩的频率分布直方图如下.
(1)如果成绩大于135分的为特别优秀,则随机抽取的500名学生中本次考试英语 数学特别优秀的大约各多少人?(假设数学成绩在频率分布直方图中各段是均匀分布)
(2)如果英语和数学两科都特别优秀的共有6人,从(1)中英语特别优秀的人中随机抽取3人,设3人中两科同时特别优秀的有人,求的分布列和数学期望.
附公式:若,则0.96.
21.(本小题满分12分)已知数列是正项等比数列,且,若数列满足.
(1)求数列和的通项公式;
(2)已知,记.若恒成立,求实数的取值范围.
22.(本小题满分12分)已知函数,其中.
(1)若,讨论函数的单调性;
(2)已知是函数的两个零点,且,证明:.
鞍山市五校2022-2023学年高二下学期期末考试
数学试卷参考答案与评分标准
一 单选题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1 2 3 4 5 6 7 8
D B D C C C B A
二 多选题(本大题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9 10 11 12
BCD BCD ABC BD
三 填空题(本大题共4小题,每小题5分,共20分)
13. 14. 15. 16.
四 解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题10分)
【解析】
(1)因为函数
所以,
因为在处的切线与直线垂直
由导数的几何意义及两条直线互相垂直条件可知,得
解得
(2)当时,,
当时,,当时,,
所以函数在区间上单调递减,在区间上单调递增,
所以当时,函数取得极小值1,无极大值.
18.(本小题12分)
【解折】
(1)依题意可得,该市一天的空气质量等级为1的概率为,
等级为2的概率为
所以“空气质量好”的概率为
所以2022年(365天)“空气质量好”的天数为(天)
因此估计沈阳市2022年(365天)“空气质显好”的天数为263天-
(2)依题意列联表如下所示:
人次 人次>400
空气质是好 35 37
空气质量不好 20 8
所以
因此没有的把握认为一天中到浑河绿道锻炼的人次与沈阳市当天的空气质量有关.
19.(本小题12分)
【解析】(1)因为,
所以,
所以,
所以数列是以1为首项,3为公比的等比数列
(2)由(1)知,因为,
所以
所以,,
两式相减,得,
所以
20.(本小遈12分)
【解析】(1),
,故英语成绩特别优秀的有人.
由频率分布直方图知,数学成绩特别优秀的频率为
故数学成绩待别优秀的有人.
(2)依题意:取值集合
其分布列为:
0 1 2 3
21.(本小题满分12分)
【解折】(1)设数列的公比为,则,
因为,由已知可得,所以,
即,解得(舍去)或,
故数列的通项公式为.
因为,所以,
又由,得,所以当时,
经检验,也满足上式,所以
(2)由(1)得,
所以
又恒成立,所以恒成立.
设
则.
易知当时,;当时,.
于是,
所以,
所以实数的取值范围是
22.(本小题满分12分)
【解析】(1)若,即,
可得,
①若,则,
即在单调递减:
②若,令有,令有
即在上单调递减,上单调递增,
综上可得:当在单调递减;
当在上单调递减,上单调递增.
(2)解:由题意知是的两个零点,且,
即,
所以,
即,
要证:,
只需证:
即证:,
即证:,令,
即证:令,
可得,
即在上单调递增,则,
即,
设,有,
所以在上单调递减,
则,即
综上可得:
同课章节目录
