平方差公式[上学期]
图片预览





文档简介
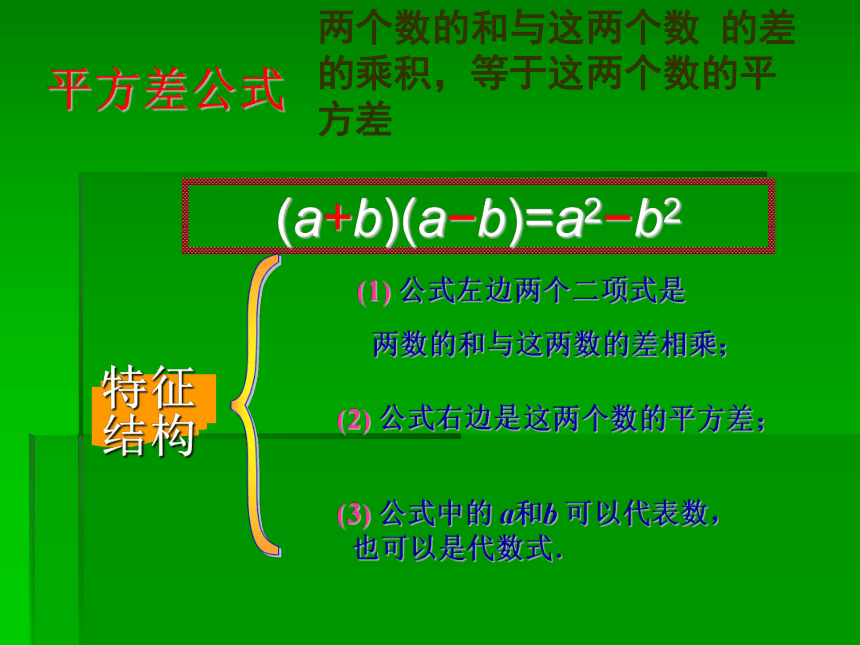
课件15张PPT。平方差公式计算下列各题,看谁做得又快又准?一、创设情境(1)(x+1)(x-1) (2)(m+2)(m-2)?(3)(2x+1)(2x-1)(4)(3m-4)(3m+4)=x 2-1=m 2-4=4x 2-1=9m 2-16(1)(x+1)(x-1) =x 2-1? (2)(m+2)(m-2) =m 2-4?(3)(2x+1)(2x-1) =4x 2-1(4)(3m-4)(3m+4) =9m 2-16探究与思考从上述的式子,你发现了什么?(a+b)(a-b)=a2-b2两个数的和与这两个数的差的积,等于这两个数的平方差.平方差公式(a+b)(a?b)=a2?b2特征
结构{(1) 公式左边两个二项式是两数的和与这两数的差相乘;(2) 公式右边是这两个数的平方差;
(3) 公式中的 a和b 可以代表数,
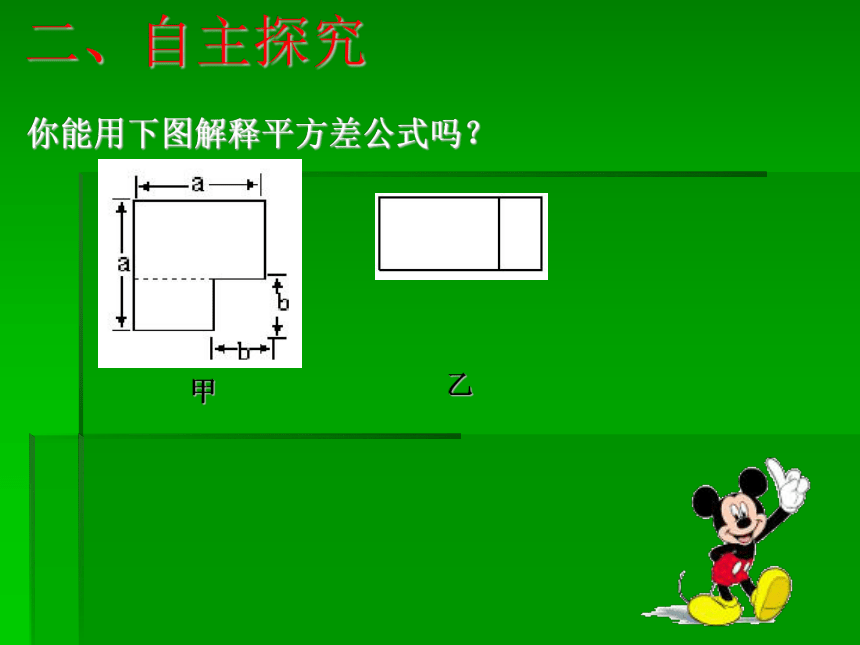
也可以是代数式.两个数的和与这两个数 的差的乘积,等于这两个数的平方差 二、自主探究你能用下图解释平方差公式吗?甲乙温岭街心公园有一块边长为a米的正方形草坪,经统一规划后,东西向要加长2米,而南北向要缩短2米,问:改造后的长方形草坪面积是多少?规划后草坪面积有没有改变?周长呢?
解:(a+2)(a-2)=a2 _2a+2a-4= a2 -4展示应用,体验成功
做一做,试一试(1)(-a+b)(-a-b)
(2) (1+2a)(1-2a)
(3) (2x+y)(2x-y)
(4)1002×998
=(-a)2-(b)2=(1)2-(2a)2=(2x)2-(y)2=(1000+2)(1000-2)=a2-b2=1-4a2=4x2-y2=10002-22=9999961、请你计算三、应用探究 协作交流 培养能力3、观察:(-2x+y)( ),在括号内填入怎样的代数式,才能运用平方差公式进行计算? 2、你能计算吗?(1)(-x-2y)(-x+2y) (2) (b+2a)(2a-b)
(3) (3a2-4b3)(3a2+4b3)(1)(3x+2)(3x-2) (2)( a+ x)( a- x)?
(3) (2a-3b)(2a+3b) (4)( ?+ )( - )四、反馈练习 巩固新知1、判断正误,如果错误,应怎样改正? ( 1 ) (-a-b)(a-b)=-a2+b2 ( )
( 2 ) (-a+b)(-a-b)=-a2-b2 ( )
( 3 ) (2x+3)(2x-3)=2x2-9 ( )
( 4 ) (3x-1)(-3x-1)=9x2-1 ( )
(5) (a+b)(-a-b)=a2-b2 ( )
(6)(2x+3)(3x-3)=6x-9 ( )1.下列多项式相乘,哪些可用平方差
公式?怎样用公式计算?
1) (a+b)(-b+a) 2) (ab+1)(-ab+1)
3) (-2xy+z)(-2xy-z) 4) (a2-3bc)(3bc+a2)
=(a+b)(a-b)=(1+ab)(1-ab)=(z-2xy)[-(z+2xy)]五 、 巩固深化2.(a+b+c)(a+b-c),是否可用平方差公式计
算?怎样应用公式计算?解: (a+b+c) (a+b-c)
= [(a+b)+c] [(a+b)-c]
= (a+b)2 - c2
= (a+b) (a+b) – c2
= (a2+ab+ab+b2) – c2
= (a2+2ab+b2) – c2
= a2+2ab+b2 – c23.下列各式哪些能用平方差公式计算?
怎样用?
(1) (a-b+c)(a-b-c) 解: (1) (a-b+c)(a-b-c)
= [ (a-b)+c] [ (a-b)-c ]
= (a-b)2 – c2
= (a2-2ab+b2) –c2
= a2-2ab+b2 –c24.计算:
(4) (x+ )(x2+ )(x- )解:4) (x+ )(x2+ )(x- )= [(x+ )(x- )](x2+ )= (x2- )(x2+ )= x4-小 结布置作业课本84页 习题14.3 第1题
再见
结构{(1) 公式左边两个二项式是两数的和与这两数的差相乘;(2) 公式右边是这两个数的平方差;
(3) 公式中的 a和b 可以代表数,
也可以是代数式.两个数的和与这两个数 的差的乘积,等于这两个数的平方差 二、自主探究你能用下图解释平方差公式吗?甲乙温岭街心公园有一块边长为a米的正方形草坪,经统一规划后,东西向要加长2米,而南北向要缩短2米,问:改造后的长方形草坪面积是多少?规划后草坪面积有没有改变?周长呢?
解:(a+2)(a-2)=a2 _2a+2a-4= a2 -4展示应用,体验成功
做一做,试一试(1)(-a+b)(-a-b)
(2) (1+2a)(1-2a)
(3) (2x+y)(2x-y)
(4)1002×998
=(-a)2-(b)2=(1)2-(2a)2=(2x)2-(y)2=(1000+2)(1000-2)=a2-b2=1-4a2=4x2-y2=10002-22=9999961、请你计算三、应用探究 协作交流 培养能力3、观察:(-2x+y)( ),在括号内填入怎样的代数式,才能运用平方差公式进行计算? 2、你能计算吗?(1)(-x-2y)(-x+2y) (2) (b+2a)(2a-b)
(3) (3a2-4b3)(3a2+4b3)(1)(3x+2)(3x-2) (2)( a+ x)( a- x)?
(3) (2a-3b)(2a+3b) (4)( ?+ )( - )四、反馈练习 巩固新知1、判断正误,如果错误,应怎样改正? ( 1 ) (-a-b)(a-b)=-a2+b2 ( )
( 2 ) (-a+b)(-a-b)=-a2-b2 ( )
( 3 ) (2x+3)(2x-3)=2x2-9 ( )
( 4 ) (3x-1)(-3x-1)=9x2-1 ( )
(5) (a+b)(-a-b)=a2-b2 ( )
(6)(2x+3)(3x-3)=6x-9 ( )1.下列多项式相乘,哪些可用平方差
公式?怎样用公式计算?
1) (a+b)(-b+a) 2) (ab+1)(-ab+1)
3) (-2xy+z)(-2xy-z) 4) (a2-3bc)(3bc+a2)
=(a+b)(a-b)=(1+ab)(1-ab)=(z-2xy)[-(z+2xy)]五 、 巩固深化2.(a+b+c)(a+b-c),是否可用平方差公式计
算?怎样应用公式计算?解: (a+b+c) (a+b-c)
= [(a+b)+c] [(a+b)-c]
= (a+b)2 - c2
= (a+b) (a+b) – c2
= (a2+ab+ab+b2) – c2
= (a2+2ab+b2) – c2
= a2+2ab+b2 – c23.下列各式哪些能用平方差公式计算?
怎样用?
(1) (a-b+c)(a-b-c) 解: (1) (a-b+c)(a-b-c)
= [ (a-b)+c] [ (a-b)-c ]
= (a-b)2 – c2
= (a2-2ab+b2) –c2
= a2-2ab+b2 –c24.计算:
(4) (x+ )(x2+ )(x- )解:4) (x+ )(x2+ )(x- )= [(x+ )(x- )](x2+ )= (x2- )(x2+ )= x4-小 结布置作业课本84页 习题14.3 第1题
再见
