沪科版数学九年级上册22.2相似三角形的判定(常见相似模型)课件 (共42张PPT)
文档属性
| 名称 | 沪科版数学九年级上册22.2相似三角形的判定(常见相似模型)课件 (共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 801.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 00:00:00 | ||
图片预览


文档简介
(共42张PPT)
沪科版九年级上册数学
常见相似模型
母子型
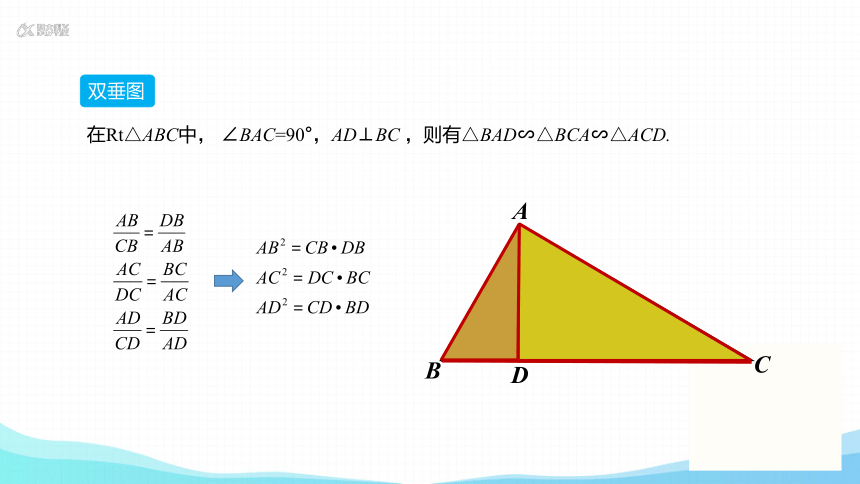
在Rt△ABC中, ∠BAC=90°,AD⊥BC ,则有△BAD∽△BCA∽△ACD.
双垂图
A
B
C
D
△BAD∽△BCA
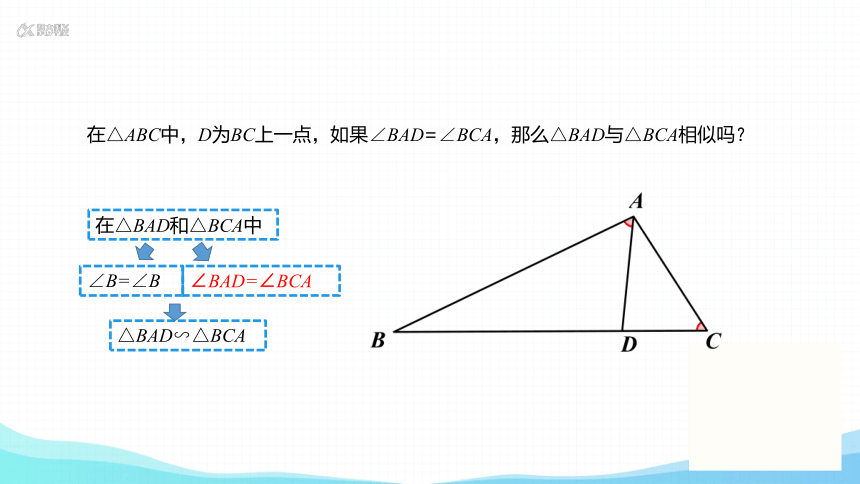
∠B=∠B
∠BAD=∠BCA
在△ABC中,D为BC上一点,如果∠BAD=∠BCA,那么△BAD与△BCA相似吗?
在△BAD和△BCA中
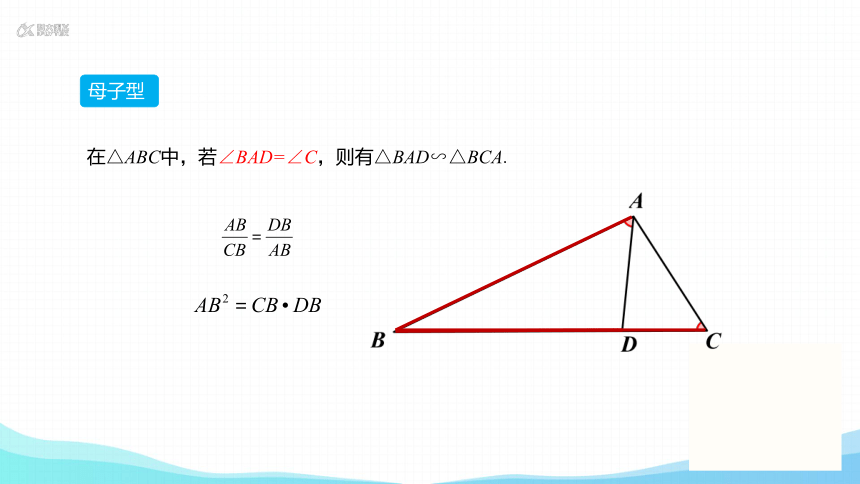
母子型
在△ABC中,若∠BAD=∠C,则有△BAD∽△BCA.
在△ABC中,若∠BAD=∠C,
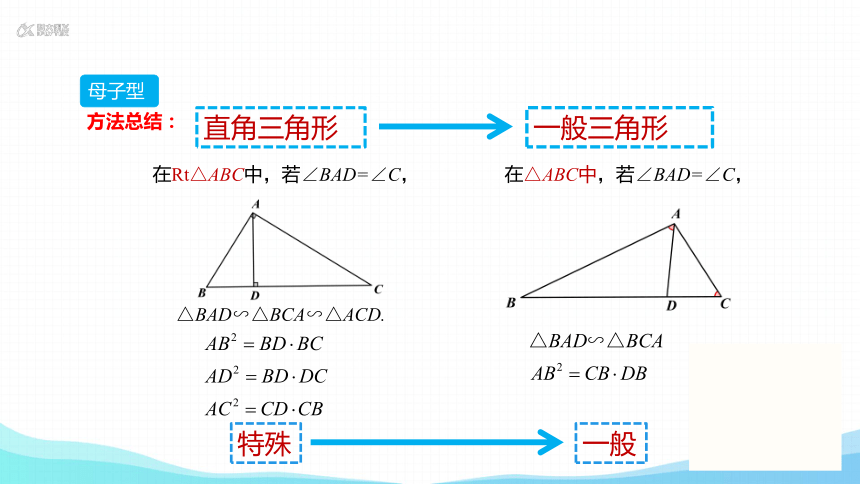
方法总结:
在Rt△ABC中,若∠BAD=∠C,
△BAD∽△BCA∽△ACD.
特殊
一般
直角三角形
一般三角形
母子型
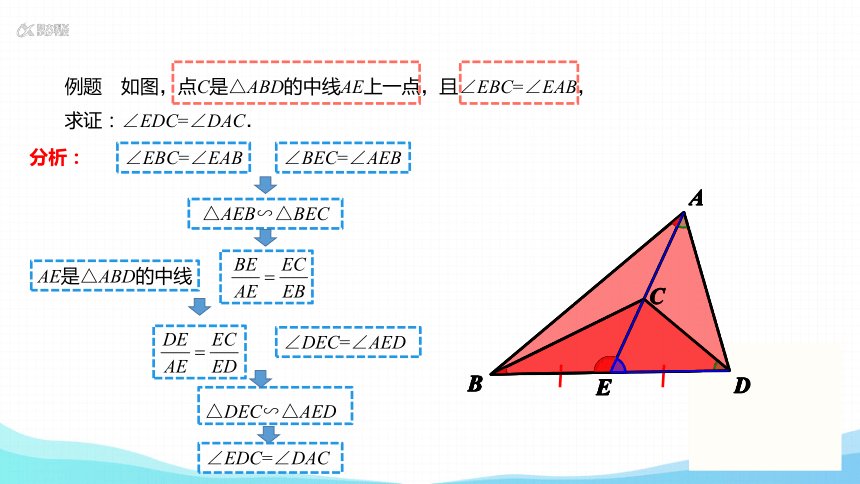
例题 如图,点C是△ABD的中线AE上一点,且∠EBC=∠EAB,
求证:∠EDC=∠DAC.
分析:
∠EBC=∠EAB
∠BEC=∠AEB
△AEB∽△BEC
AE是△ABD的中线
∠DEC=∠AED
△DEC∽△AED
∠EDC=∠DAC
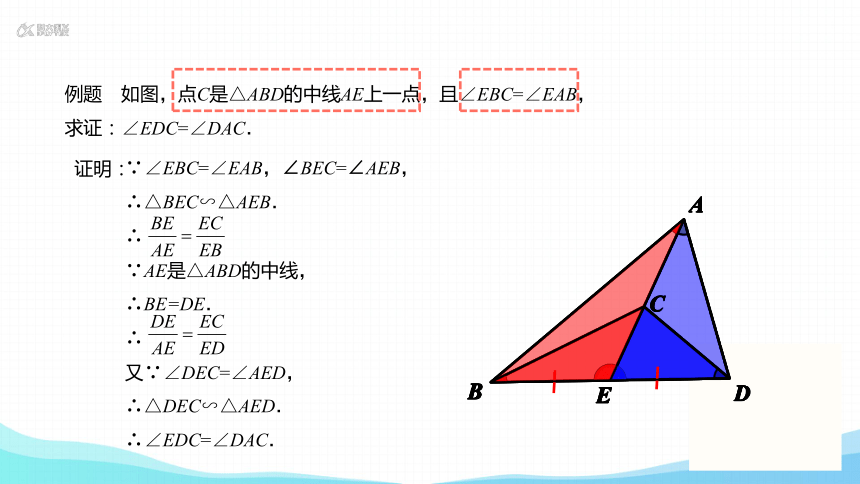
例题 如图,点C是△ABD的中线AE上一点,且∠EBC=∠EAB,
求证:∠EDC=∠DAC.
证明:
∵∠EBC=∠EAB,∠BEC=∠AEB,
∴△BEC∽△AEB.
∴
∵AE是△ABD的中线,
∴BE=DE.
∴
又∵∠DEC=∠AED,
∴△DEC∽△AED.
∴∠EDC=∠DAC.
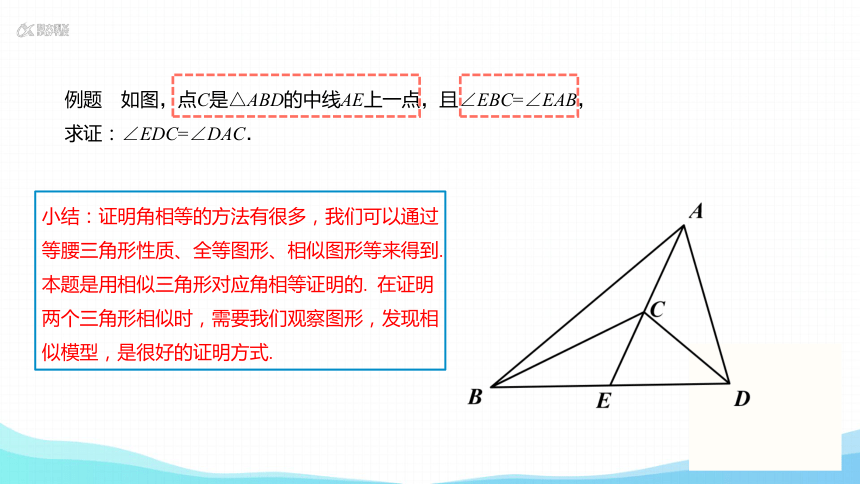
例题 如图,点C是△ABD的中线AE上一点,且∠EBC=∠EAB,
求证:∠EDC=∠DAC.
小结:证明角相等的方法有很多,我们可以通过等腰三角形性质、全等图形、相似图形等来得到.本题是用相似三角形对应角相等证明的. 在证明两个三角形相似时,需要我们观察图形,发现相似模型,是很好的证明方式.
分析:
∠ACB=∠BCE
∠BEC=∠BCE.
BE=BC
CD=ED,BD⊥AC
∠ABC=∠BEC.
AB=AC.
∠ABC=∠ACB.
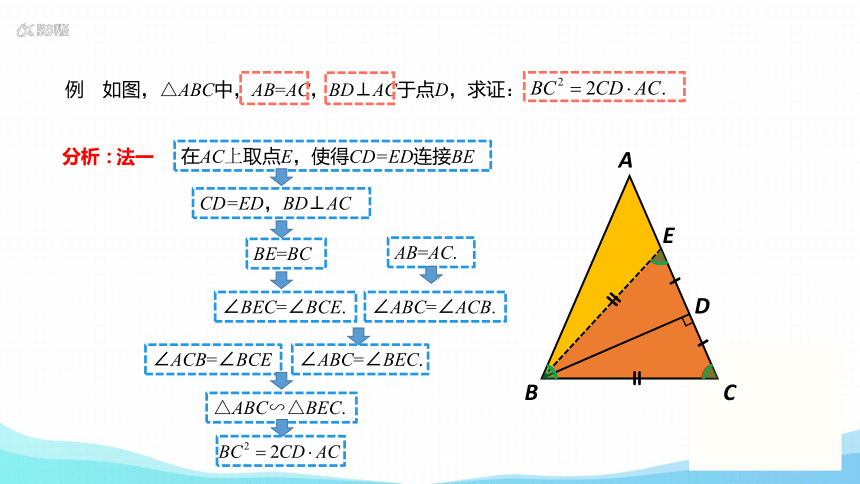
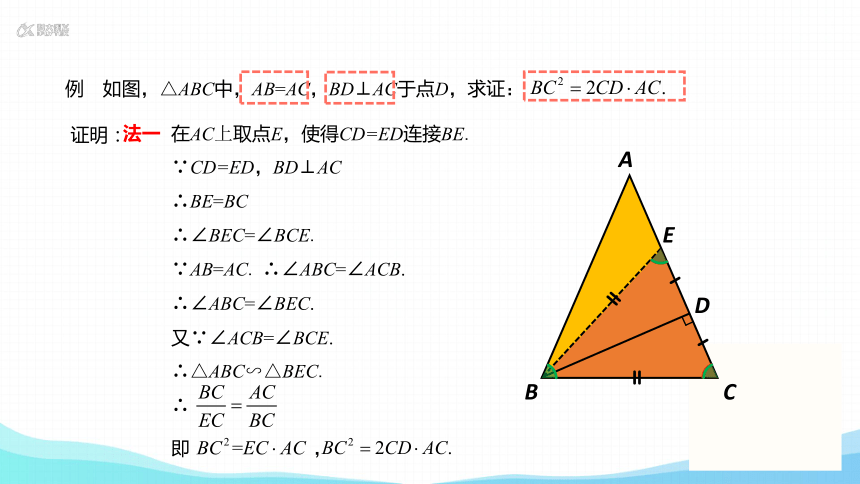
例 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
在AC上取点E,使得CD=ED连接BE
△ABC∽△BEC.
A
B
C
D
E
法一
在AC上取点E,使得CD=ED连接BE.
∵CD=ED,BD⊥AC
∴BE=BC
∴∠BEC=∠BCE.
∵AB=AC. ∴∠ABC=∠ACB.
∴∠ABC=∠BEC.
又∵∠ACB=∠BCE.
∴△ABC∽△BEC.
∴
即 ,
例 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
A
B
C
D
E
证明:
法一
例 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
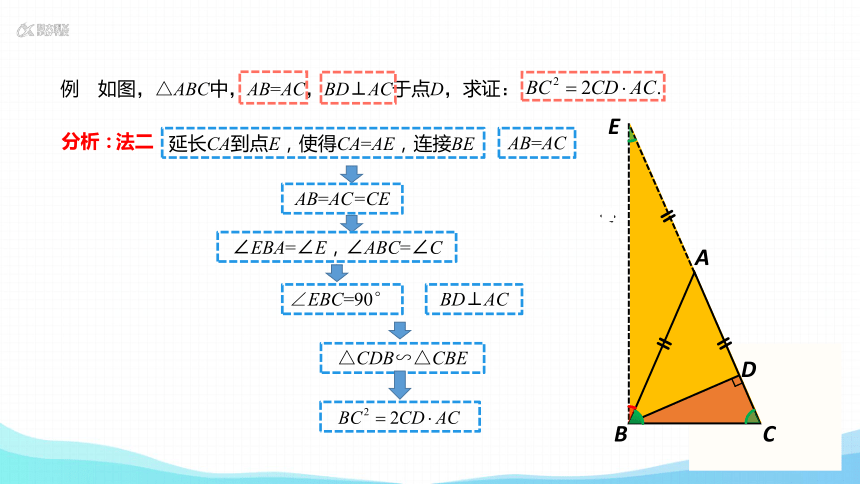
分析:
法二
A
B
C
D
E
AB=AC
延长CA到点E,使得CA=AE,连接BE
AB=AC=CE
∠EBA=∠E,∠ABC=∠C
BD⊥AC
∠EBC=90°
△CDB∽△CBE
延长CA到点E,使得CA=AE,连接BE.
∴∠EBA=∠E
∵AB=AC. ∴∠ABC=∠ACB.
∴∠EBC=90°
∵ BD⊥AC于点D , ∴∠BDC=90°.
∴△CDB∽△CBE.
∴ CD:CB=CB:CE
∴ ,又CE=2AC ∴BC =2CD·AC
例 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
A
B
C
D
E
证明:
法二
例 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
A
B
C
D
E
小结:在证明线段之间积的关系时,我们往往会用到相似三角形对应边的成比例的性质. 根据结论乘积式的特征,添加辅助线,构造常见相似模型母子型相似图形,往往是证明相似的很好方式.
一线三等角
二、一线三等角
△ABC和△CDE是直角三角形,若∠ACE=90°,
则有△ABC ∽△CDE.
二、一线三等角
△ABC ∽△CDE
在△ABC和△CDE中
∠B=∠D
∠BAC=∠ECD
△ABC和△CDE是任意三角形,若∠B=∠ACE=∠D,△ABC 和△CDE相似吗
∠B=∠ACE
二、一线三等角
△ABC和△CDE是任意三角形,若
∠B=∠ACE=∠D,则有△ABC ∽△CDE.
方法总结:
△ABC和△CDE是直角三角形,若∠ACE=90°,则有△ABC ∽△CDE.
.
特殊
一般
直角三角形
一般三角形
二、一线三等角
方法总结:
△ABC和△CDE是任意三角形,若∠B=∠ACE=∠D,则有△ABC ∽△CDE.
有三个等角的顶点在同一条直线上构成的相似图形.
异侧
同侧
一线三等角
同侧:两个三角形在直线同侧
异侧:两个三角形在直线两侧
△ABC和△CDE是任意三角形,若
∠B=∠ACE=∠D,则有△ABC ∽△CDE.
△ABC和△CDE是直角三角形,若∠ACE=90°,则有△ABC ∽△CDE.
.
特殊
一般
直角三角形
一般三角形
一线三等角
例题 在△ABC中,∠ABC=∠EFD=45°,AB= ,AD=AE,∠DAE=90°,CE= ,
求CD的长.
分析:
∠ADE=45°
△ABD∽△DFE
DF=4
CD=5
A
B
C
D
E
F
求证∠CEF=∠CDE
△CEF∽△CDE
4
例题 在△ABC中,∠ABC=∠EFD=45°,AB= ,AD=AE,∠DAE=90°,CE= ,
求CD的长.
∵AD=AE,∠DAE=90°,
∴∠AED=∠ADE=45°.
∵∠ADE+∠EDF=∠B+∠BAD ,∠B =45°.
∴∠BAD=∠EDF 又 ∠ABC=∠EFD=45°
∴△BAD∽△FDE.
∴
又∵ AB=
∴DF=4.
A
B
C
D
E
F
4
证明:
∵∠CEF+∠FED+∠AED=180°,∠AED=∠DFE=45°且∠DFE+∠FED +∠FDE=180°
∴∠CEF=∠FDE
例题 在△ABC中,∠ABC=∠EFD=45°,AB= ,AD=AE,∠DAE=90°,CE= ,
求CD的长.
A
B
C
D
E
F
4
证明:
又 ∵∠C=∠C ∴△CEF∽△CDE
∴CE:CF=CD:CE
∴CE2=CF·DC
设CF=x,则CD=x+4
∵
∴x(x+4)=5
x2+4x=5
x2+4x-5=0
(x-1)(x+5)=0
x1=-5(舍)
x2=1
∴CF=1,CD=5
例题 在△ABC中,∠ABC=∠EFD=45°,AB= ,AD=AE,∠DAE=90°,CE= ,
求CD的长.
A
B
C
D
E
F
小结:在几何证明中,有时候一次的相似并不能让我们直接得到结论,需要将相似中得到的结论,运用到证明新的相似中去,这样一个循环过程,从而完成证明. 如果我们能够先观察图形特征,发现常见相似模型,将给我们的证明带来事半功倍的效果.
例题 在平行四边形ABCD中,AB=6,BC=8,E、F分别为BC、AB上的点,∠DEF=∠B=60°, DF⊥EF于F,求AF的长.
分析:
∠DGC=60°
延长BC到点G使得CG=CD,连接DG.
△BFE∽△GED
DF⊥EF,∠DEF=60°
BE=3
EG=11
A
B
C
D
F
E
G
6
8
3
11
例题 在平行四边形ABCD中,AB=6,BC=8,E、F分别为BC、AB上的点,∠DEF=∠B=60°, DF⊥EF于F,求AF的长.
A
B
C
D
F
E
G
3
11
证明:
∴BE=3,又BG=BC+CG=6+8=14
∴EG=11
∴
延长BC到点G使得CG=CD,连接DG
∴∠DCG=∠B=60°,AB=CD=6,
∵四边形ABCD是平行四边形,
∴△CGD是等腰三角形,∠DGC=60°,
∵∠B+∠BFE=∠FED+∠DEG,
又∵∠B=∠FED,
∵△BFE∽∠GED,
∴∠BFE=∠DEG,
∵DE⊥EF,∠DEF=60°∴∠FDE=30°,
∴ ,又CG=CD=DG=6.
例题 在平行四边形ABCD中,AB=6,BC=8,E、F分别为BC、AB上的点,∠DEF=∠B=60°, DF⊥EF于F,求AF的长.
A
B
C
D
F
E
G
小结:这是一道证明线段长的问题,我们可以利用相似三角形对应边成比例,来求出线段长度,有的时候往往在题目中找不到相似模型,这就需要构造常见相似模型. 本题我们构造了一线三等角模型,从而求出线段长.
手拉手
△ABC中,DE // BC,则有△ADE∽△ABC .
手拉手
如图△ADE∽△ABC,△ABD 和△ACE 相似吗?
旋转
手拉手
如图△ADE∽△ABC,△ABD 和△ACE 相似吗?
手拉手
△ABD∽△ACE
△ADE∽△ABC
∠BAC=∠DAE
∠1=∠3
如图△ADE∽△ABC,△ABD 和△ACE 相似吗?
手拉手
如图△ADE∽△ABC,△ABD∽△ACE.
旋转
方法总结:
两个具有公共顶点的相似三角形,连结对应顶点所构成的两三角形相似,称为“手拉手相似模型”.
手拉手
例题 如图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,E是AB边上的一点,∠ECF=90°,∠CEF=∠B, AF=3时,求BE 的长.
分析:
在Rt△ABC,∠ACB=90°,AC=6,AB=10
∠CEF=∠B
BC=8;
△ABC ∽△FEC
∠ECB=∠FCA
△BCE∽△ACF.
BE=4.
∠ACB=∠FCE=90°
证明:∵在Rt△ABC,∠ACB=90°,AC=6,AB=10
∴BC=8;∠ACB=∠FCE=90°.
又∵∠CEF=∠B ∴△ABC ∽△FEC.
又∵∠ACB=∠FCE=90°,
∠ACB-∠ACE=∠FCE-∠ACE.
∴∠ECB=∠FCA.
∴
∴
例题 如图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,E是AB边上的一点,∠ECF=90°,∠CEF=∠B, AF=3时,求BE 的长.
∴△BCE∽△ACF.
小结:观察图形,发现旋转相似,利用手拉手相似三角形求线段长度.
∴
∴
∴
∴BE=4.
例题 如图,在四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,且满足AC= AB,求证:
分析:
将△ADC绕点A顺时针旋转,使得AD与AB重合,得到△ABE,连接CE
∠EBC=90°
∠BAD+∠BCD=90°
∠ABC+∠ADC=∠ABC+∠ABE=270°
CE= BD.
△ABD∽△AEC,
例题 如图,在四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,且满足AC= AB,求证:
分析:
将△ADC绕点A顺时针旋转,使得AD与AB重合,得到△ABE,连接CE
∠EBC=90°
∠BAD+∠BCD=90°
∠ABC+∠ADC=∠ABC+∠ABE=270°
CE= BD.
△ABD∽△AEC,
例题 如图,在四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,且满足AC= AB,求证:
将△ADC绕点A顺时针旋转,使得AD与AB重合,
得到△ABE,连接CE
∵△ADC≌△ABE,
∴AC=AE,∠DAC=∠BAE.
∴∠DAC+∠BAC=∠BAE+∠BAC,
即∠BAD=∠EAC.
证明:
∴△ABD∽△AEC,
∴CE:BD=AC:AD=
∴CE= BD.
例题 如图,在四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,且满足AC= AB,求证:
将△ADC绕点A顺时针旋转,使得AD与AB重合,
得到△ABE,连接CE
证明:
∵在四边形ABCD中,内角和为360°,
且∠BAD+∠BCD=90°.
∴∠ABC+∠ADC=∠ABC+∠ABE=270°,
∴∠EBC=90°,
∴在Rt△BCE中,
小结:从动态角度可以利用旋转变换,将分散的角度、线段集中. 利用图形旋转变换,构造手拉手模型,利用对应边成比例,求出线段长度.
总结
常见相似模型
母子型
手拉手
一线三等角
特殊到一般
特殊到一般
旋转
观察图形特征
构造基础模型
再 见
沪科版九年级上册数学
常见相似模型
母子型
在Rt△ABC中, ∠BAC=90°,AD⊥BC ,则有△BAD∽△BCA∽△ACD.
双垂图
A
B
C
D
△BAD∽△BCA
∠B=∠B
∠BAD=∠BCA
在△ABC中,D为BC上一点,如果∠BAD=∠BCA,那么△BAD与△BCA相似吗?
在△BAD和△BCA中
母子型
在△ABC中,若∠BAD=∠C,则有△BAD∽△BCA.
在△ABC中,若∠BAD=∠C,
方法总结:
在Rt△ABC中,若∠BAD=∠C,
△BAD∽△BCA∽△ACD.
特殊
一般
直角三角形
一般三角形
母子型
例题 如图,点C是△ABD的中线AE上一点,且∠EBC=∠EAB,
求证:∠EDC=∠DAC.
分析:
∠EBC=∠EAB
∠BEC=∠AEB
△AEB∽△BEC
AE是△ABD的中线
∠DEC=∠AED
△DEC∽△AED
∠EDC=∠DAC
例题 如图,点C是△ABD的中线AE上一点,且∠EBC=∠EAB,
求证:∠EDC=∠DAC.
证明:
∵∠EBC=∠EAB,∠BEC=∠AEB,
∴△BEC∽△AEB.
∴
∵AE是△ABD的中线,
∴BE=DE.
∴
又∵∠DEC=∠AED,
∴△DEC∽△AED.
∴∠EDC=∠DAC.
例题 如图,点C是△ABD的中线AE上一点,且∠EBC=∠EAB,
求证:∠EDC=∠DAC.
小结:证明角相等的方法有很多,我们可以通过等腰三角形性质、全等图形、相似图形等来得到.本题是用相似三角形对应角相等证明的. 在证明两个三角形相似时,需要我们观察图形,发现相似模型,是很好的证明方式.
分析:
∠ACB=∠BCE
∠BEC=∠BCE.
BE=BC
CD=ED,BD⊥AC
∠ABC=∠BEC.
AB=AC.
∠ABC=∠ACB.
例 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
在AC上取点E,使得CD=ED连接BE
△ABC∽△BEC.
A
B
C
D
E
法一
在AC上取点E,使得CD=ED连接BE.
∵CD=ED,BD⊥AC
∴BE=BC
∴∠BEC=∠BCE.
∵AB=AC. ∴∠ABC=∠ACB.
∴∠ABC=∠BEC.
又∵∠ACB=∠BCE.
∴△ABC∽△BEC.
∴
即 ,
例 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
A
B
C
D
E
证明:
法一
例 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
分析:
法二
A
B
C
D
E
AB=AC
延长CA到点E,使得CA=AE,连接BE
AB=AC=CE
∠EBA=∠E,∠ABC=∠C
BD⊥AC
∠EBC=90°
△CDB∽△CBE
延长CA到点E,使得CA=AE,连接BE.
∴∠EBA=∠E
∵AB=AC. ∴∠ABC=∠ACB.
∴∠EBC=90°
∵ BD⊥AC于点D , ∴∠BDC=90°.
∴△CDB∽△CBE.
∴ CD:CB=CB:CE
∴ ,又CE=2AC ∴BC =2CD·AC
例 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
A
B
C
D
E
证明:
法二
例 如图,△ABC中,AB=AC,BD⊥AC于点D,求证:
A
B
C
D
E
小结:在证明线段之间积的关系时,我们往往会用到相似三角形对应边的成比例的性质. 根据结论乘积式的特征,添加辅助线,构造常见相似模型母子型相似图形,往往是证明相似的很好方式.
一线三等角
二、一线三等角
△ABC和△CDE是直角三角形,若∠ACE=90°,
则有△ABC ∽△CDE.
二、一线三等角
△ABC ∽△CDE
在△ABC和△CDE中
∠B=∠D
∠BAC=∠ECD
△ABC和△CDE是任意三角形,若∠B=∠ACE=∠D,△ABC 和△CDE相似吗
∠B=∠ACE
二、一线三等角
△ABC和△CDE是任意三角形,若
∠B=∠ACE=∠D,则有△ABC ∽△CDE.
方法总结:
△ABC和△CDE是直角三角形,若∠ACE=90°,则有△ABC ∽△CDE.
.
特殊
一般
直角三角形
一般三角形
二、一线三等角
方法总结:
△ABC和△CDE是任意三角形,若∠B=∠ACE=∠D,则有△ABC ∽△CDE.
有三个等角的顶点在同一条直线上构成的相似图形.
异侧
同侧
一线三等角
同侧:两个三角形在直线同侧
异侧:两个三角形在直线两侧
△ABC和△CDE是任意三角形,若
∠B=∠ACE=∠D,则有△ABC ∽△CDE.
△ABC和△CDE是直角三角形,若∠ACE=90°,则有△ABC ∽△CDE.
.
特殊
一般
直角三角形
一般三角形
一线三等角
例题 在△ABC中,∠ABC=∠EFD=45°,AB= ,AD=AE,∠DAE=90°,CE= ,
求CD的长.
分析:
∠ADE=45°
△ABD∽△DFE
DF=4
CD=5
A
B
C
D
E
F
求证∠CEF=∠CDE
△CEF∽△CDE
4
例题 在△ABC中,∠ABC=∠EFD=45°,AB= ,AD=AE,∠DAE=90°,CE= ,
求CD的长.
∵AD=AE,∠DAE=90°,
∴∠AED=∠ADE=45°.
∵∠ADE+∠EDF=∠B+∠BAD ,∠B =45°.
∴∠BAD=∠EDF 又 ∠ABC=∠EFD=45°
∴△BAD∽△FDE.
∴
又∵ AB=
∴DF=4.
A
B
C
D
E
F
4
证明:
∵∠CEF+∠FED+∠AED=180°,∠AED=∠DFE=45°且∠DFE+∠FED +∠FDE=180°
∴∠CEF=∠FDE
例题 在△ABC中,∠ABC=∠EFD=45°,AB= ,AD=AE,∠DAE=90°,CE= ,
求CD的长.
A
B
C
D
E
F
4
证明:
又 ∵∠C=∠C ∴△CEF∽△CDE
∴CE:CF=CD:CE
∴CE2=CF·DC
设CF=x,则CD=x+4
∵
∴x(x+4)=5
x2+4x=5
x2+4x-5=0
(x-1)(x+5)=0
x1=-5(舍)
x2=1
∴CF=1,CD=5
例题 在△ABC中,∠ABC=∠EFD=45°,AB= ,AD=AE,∠DAE=90°,CE= ,
求CD的长.
A
B
C
D
E
F
小结:在几何证明中,有时候一次的相似并不能让我们直接得到结论,需要将相似中得到的结论,运用到证明新的相似中去,这样一个循环过程,从而完成证明. 如果我们能够先观察图形特征,发现常见相似模型,将给我们的证明带来事半功倍的效果.
例题 在平行四边形ABCD中,AB=6,BC=8,E、F分别为BC、AB上的点,∠DEF=∠B=60°, DF⊥EF于F,求AF的长.
分析:
∠DGC=60°
延长BC到点G使得CG=CD,连接DG.
△BFE∽△GED
DF⊥EF,∠DEF=60°
BE=3
EG=11
A
B
C
D
F
E
G
6
8
3
11
例题 在平行四边形ABCD中,AB=6,BC=8,E、F分别为BC、AB上的点,∠DEF=∠B=60°, DF⊥EF于F,求AF的长.
A
B
C
D
F
E
G
3
11
证明:
∴BE=3,又BG=BC+CG=6+8=14
∴EG=11
∴
延长BC到点G使得CG=CD,连接DG
∴∠DCG=∠B=60°,AB=CD=6,
∵四边形ABCD是平行四边形,
∴△CGD是等腰三角形,∠DGC=60°,
∵∠B+∠BFE=∠FED+∠DEG,
又∵∠B=∠FED,
∵△BFE∽∠GED,
∴∠BFE=∠DEG,
∵DE⊥EF,∠DEF=60°∴∠FDE=30°,
∴ ,又CG=CD=DG=6.
例题 在平行四边形ABCD中,AB=6,BC=8,E、F分别为BC、AB上的点,∠DEF=∠B=60°, DF⊥EF于F,求AF的长.
A
B
C
D
F
E
G
小结:这是一道证明线段长的问题,我们可以利用相似三角形对应边成比例,来求出线段长度,有的时候往往在题目中找不到相似模型,这就需要构造常见相似模型. 本题我们构造了一线三等角模型,从而求出线段长.
手拉手
△ABC中,DE // BC,则有△ADE∽△ABC .
手拉手
如图△ADE∽△ABC,△ABD 和△ACE 相似吗?
旋转
手拉手
如图△ADE∽△ABC,△ABD 和△ACE 相似吗?
手拉手
△ABD∽△ACE
△ADE∽△ABC
∠BAC=∠DAE
∠1=∠3
如图△ADE∽△ABC,△ABD 和△ACE 相似吗?
手拉手
如图△ADE∽△ABC,△ABD∽△ACE.
旋转
方法总结:
两个具有公共顶点的相似三角形,连结对应顶点所构成的两三角形相似,称为“手拉手相似模型”.
手拉手
例题 如图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,E是AB边上的一点,∠ECF=90°,∠CEF=∠B, AF=3时,求BE 的长.
分析:
在Rt△ABC,∠ACB=90°,AC=6,AB=10
∠CEF=∠B
BC=8;
△ABC ∽△FEC
∠ECB=∠FCA
△BCE∽△ACF.
BE=4.
∠ACB=∠FCE=90°
证明:∵在Rt△ABC,∠ACB=90°,AC=6,AB=10
∴BC=8;∠ACB=∠FCE=90°.
又∵∠CEF=∠B ∴△ABC ∽△FEC.
又∵∠ACB=∠FCE=90°,
∠ACB-∠ACE=∠FCE-∠ACE.
∴∠ECB=∠FCA.
∴
∴
例题 如图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,E是AB边上的一点,∠ECF=90°,∠CEF=∠B, AF=3时,求BE 的长.
∴△BCE∽△ACF.
小结:观察图形,发现旋转相似,利用手拉手相似三角形求线段长度.
∴
∴
∴
∴BE=4.
例题 如图,在四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,且满足AC= AB,求证:
分析:
将△ADC绕点A顺时针旋转,使得AD与AB重合,得到△ABE,连接CE
∠EBC=90°
∠BAD+∠BCD=90°
∠ABC+∠ADC=∠ABC+∠ABE=270°
CE= BD.
△ABD∽△AEC,
例题 如图,在四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,且满足AC= AB,求证:
分析:
将△ADC绕点A顺时针旋转,使得AD与AB重合,得到△ABE,连接CE
∠EBC=90°
∠BAD+∠BCD=90°
∠ABC+∠ADC=∠ABC+∠ABE=270°
CE= BD.
△ABD∽△AEC,
例题 如图,在四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,且满足AC= AB,求证:
将△ADC绕点A顺时针旋转,使得AD与AB重合,
得到△ABE,连接CE
∵△ADC≌△ABE,
∴AC=AE,∠DAC=∠BAE.
∴∠DAC+∠BAC=∠BAE+∠BAC,
即∠BAD=∠EAC.
证明:
∴△ABD∽△AEC,
∴CE:BD=AC:AD=
∴CE= BD.
例题 如图,在四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC,BD为对角线,且满足AC= AB,求证:
将△ADC绕点A顺时针旋转,使得AD与AB重合,
得到△ABE,连接CE
证明:
∵在四边形ABCD中,内角和为360°,
且∠BAD+∠BCD=90°.
∴∠ABC+∠ADC=∠ABC+∠ABE=270°,
∴∠EBC=90°,
∴在Rt△BCE中,
小结:从动态角度可以利用旋转变换,将分散的角度、线段集中. 利用图形旋转变换,构造手拉手模型,利用对应边成比例,求出线段长度.
总结
常见相似模型
母子型
手拉手
一线三等角
特殊到一般
特殊到一般
旋转
观察图形特征
构造基础模型
再 见
