黑龙江省龙西北八校联合体2022-2023学年高二下学期期末考试数学试题(Word版含答案)
文档属性
| 名称 | 黑龙江省龙西北八校联合体2022-2023学年高二下学期期末考试数学试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 583.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 23:11:21 | ||
图片预览



文档简介
龙西北八校联合体2022-2023学年高二下学期期末考试
数学试题
第Ⅰ卷(选择题共60分)
一、选择题:(本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知集合,则( )
A. B. C. D.
2.已知为复数且(i为虚数单位),则共轭复数的虚部为( )
A.2 B. C. D.
3.已知向量,若,则在上的投影向量的坐标为( )
A. B. C. D.
4.下图展现给我们的是唐代著名诗人杜牧写的《清明》,这首诗不仅意境极好,而且还准确地描述出了清明时节的天气状况,那就是“雨纷纷”,即天气多阴雨.某地区气象监测资料表明,清明节当天下雨的概率是0.9,连续两天下雨的概率是0.63,若该地某年清明节当天下雨,则随后一天也下雨的概率是( )
A.0.63 B.0.7 C.0.9 D.0.567
5.为了得到函数的图象,只需要把函数的图象上( )
A.各点的横坐标缩短到原来的,再向左平移个单位长度
B.各点的横坐标缩短到原来的,再向左平移个单位长度
C.各点的横坐标伸长到原来的倍,再向左平移个单位长度
D.各点的横坐标伸长到原来的2倍,再向左平移个单位长度
6.下列说法中,正确的命题是( )
A.已知随机变量服从正态分布,则
B.线性相关系数越大,两个变量的线性相关性越强,反之,线性相关性越弱
C.已知两个变量具有线性相关关系,其回归方程为,若,则
D.若样本数据的方差为8,则数据的方差为2
7.在三棱锥中,平面,且.若三棱锥的外接球体积为,则当该三棱锥的体积最大时,其表面积为( )
A. B. C. D.
8.设某工厂有两个车间生产同型号家用电器,第一车间的合格率为0.85,第二车间的合格率为0.88,两个车间的成品都混合堆放在一个仓库,假设第一,二车间生产的成品比例为2∶3,今有一客户从成品仓库中随机提一台产品,则该产品合格的概率为( )
A.0.6 B.0.85 C.0.868 D.0.88
二、多项选择题:(本题共4小题,每小题5,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分。)
9.在公比为整数的等比数列中,是数列的前项和,若,则下列说法正确的是( )
A. B.数列是等比数列
C. D.数列是公差为2的等差数列
10.下列说法正确的是( )
A.在一组样本数据的散点图中,若所有样本点都在直线上,则这组数据的样本相关系数为1
B.若变量的样本相关系数为0,则x与不存在相关关系
C.若以模型拟合一组样本数据,设,将样本数据进行相应变换后算得回归直线的方程为,则的估计值分别为和0.5
D.在回归分析中,相关指数的值越大,说明模型拟合的效果越好
11.已知是自然对数的底数,则下列不等关系中不正确的是( )
A. B. C. D.
12.已知函数,则下列结论中正确的有( )
A.必有唯一极值点
B.若,则在上单调递增
C.若,对有恒成立,则
D.若存在,使得成立,则
第Ⅱ卷(共90分)
三、填空题:(本大题共4小题,每小题5分,共20分,)
13.设随机变量,且,则________.
14.已知的展开式中第5项与第7项的二项式系数相等,且展开式的各项系数之和为1024,则展开式中含的项的系数为________.
15.如图所示的五个区域中,中心区域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色且相邻区域所涂颜色不同,则不同的涂色方法种数为________.
16.已知关于的不等式恒成立,则的取值范围为________.
四、解答题:(本大题共6小题,共70分。解答应写出必要的文字说明、证明过程或演算步骤。)
17.(本题10分)已知函数,其中为常数.
(1)当函数的图象在点处的切线的斜率为1时,求的值;
(2)在(1)的条件下,求函数在上的最小值.
18.(本题12分)一个袋子里装有除颜色以外完全相同的白球和黑球共10个.若从中不放回地取球,每次取1个球,在第一次取出黑球的条件下,第二次取出白球的概率为.
(1)求白球和黑球各有多少个;
(2)若有放回地从袋中随机摸出3个球,求恰好摸到2个黑球的概率;
(3)若不放回地从袋中随机摸出2个球,用表示摸出的黑球个数,求的分布列和期望.
19.(本题12分)已知函数,其中
(1)若函数在处取得极值,求实数的值;
(2)若函数在上恒成立,求实数的取值范围.
20.(本题12分)某中学是走读中学,为了让学生更有效率的利用下午放学后的时间,学校在本学期第一次月考后设立了多间自习室,以便让学生在自习室自主学习、完成作业,同时每天派老师轮流值班.在本学期第二次月考后,高一某班数学老师统计了两次考试该班数学成绩优良人数和非优良人数,得到如下列联表:(单位:人)
是否设立自习室 成绩 合计
非优良 优良
未设立自习室 26 14 40
设立自习室 10 30 40
合计 36 44 80
(1)依据小概率值的独立性检验,能否认为设立自习室对提高学生成绩有效?
(2)设从该班第一次月考的所有数学成绩中任取两个,取到成绩优良数为:从该班第二次月考的所有数学成绩中任取两个,取到成绩优良数为,求与的均值并比较大小,请解释所得结论的实际含义.下面的临界值表供参考:
(参考公式:,其中)
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
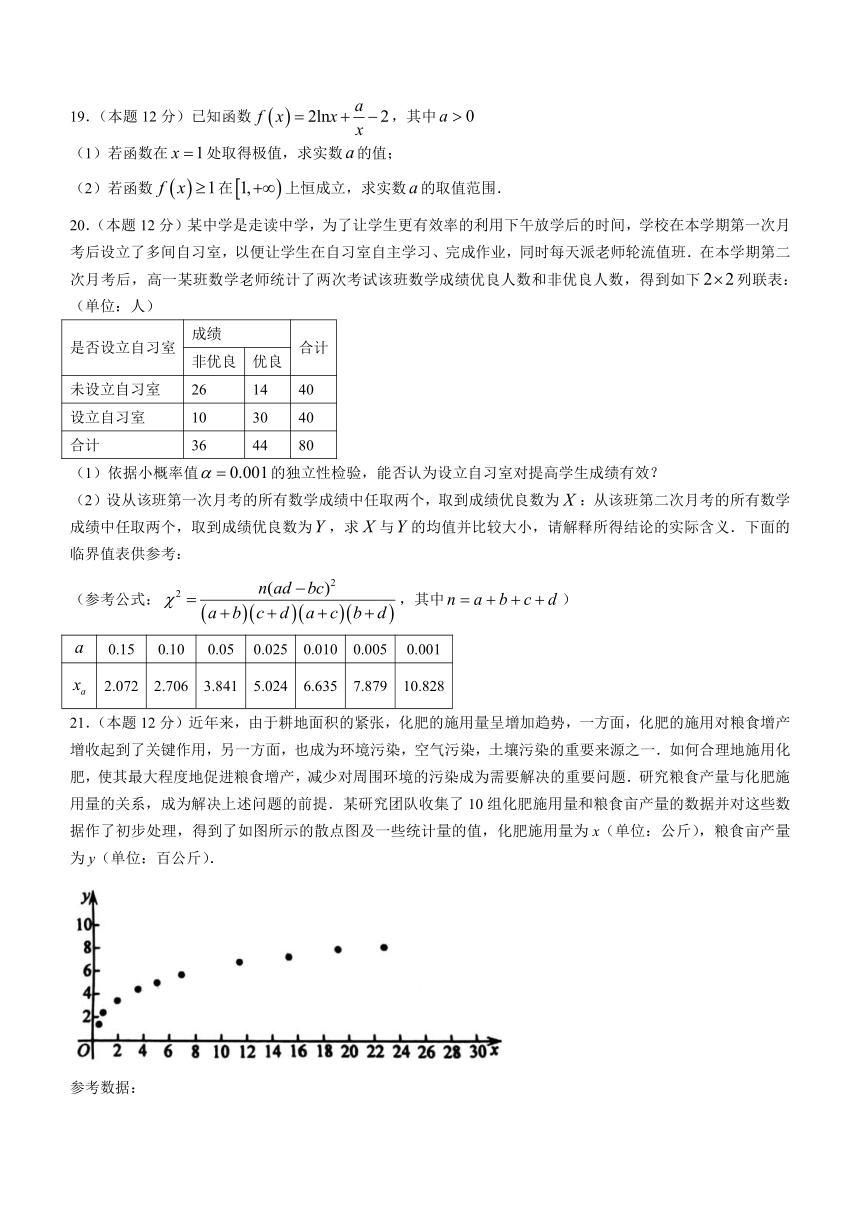
21.(本题12分)近年来,由于耕地面积的紧张,化肥的施用量呈增加趋势,一方面,化肥的施用对粮食增产增收起到了关键作用,另一方面,也成为环境污染,空气污染,土壤污染的重要来源之一.如何合理地施用化肥,使其最大程度地促进粮食增产,减少对周围环境的污染成为需要解决的重要问题.研究粮食产量与化肥施用量的关系,成为解决上述问题的前提.某研究团队收集了10组化肥施用量和粮食亩产量的数据并对这些数据作了初步处理,得到了如图所示的散点图及一些统计量的值,化肥施用量为x(单位:公斤),粮食亩产量为y(单位:百公斤).
参考数据:
650 91.5 52.5 1478.6 30.5 15 15 46.5
表中.
(1)根据散点图判断与,哪一个适宜作为粮食亩产量关于化肥施用量的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;并预测化肥施用量为27公斤时,粮食亩产量的值;
(3)经生产技术提高后,该化肥的有效率Z大幅提高,经试验统计得Z大致服从正态分布,那这种化肥的有效率超过的概率约为多少?
附:①对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为:
②若随机变量,则有
;
③取.
22.(本题12分)已知函数.
(1)当时,求函数的单调区间;
(2)当时,求使不等式恒成立的最大整数的值.
龙西北八校联合体2022-2023学年高二下学期期末考试
数学答案
一、选择题(每小题5分,共40分。)
1.C 2.C 3.C 4.B 5.B 6.D 7.C 8.C
二、多项选择题(本题共4小题,每小题5分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分。)
9.ABC 10.ACD 11.AC 12.BD
三、填空题(本题共4个小题,每小题5分,共20分。)
13.21.6 14.45 15.84 16.
17.(1)函数的定义域为,求导得,
因函数的图象在点处的切线的斜率为1,则解得,
所以的值是1.
(2)由(1)得
由,得或
因,则当时,
当时,
因此函数在上单调递减,在上单调递增
所以函数在上的最小值
18.(1)设袋中有黑球个,则白球有个,
设取出黑球为事件,取出白球的事件为,
解得,所以白球有4个,黑球有6个;
(2)由(1)知摸出黑球的概率是
则有放回地从袋中随机摸出3个球,恰好摸到2个黑球的概率为
(3)的可能取值为则
,
的分布列为:
0 1 2
19.(1)依题意,函数的定义域为,求导得:,
因函数在处取得极值,
则有,解得,此时,
当时,,当时,
因此,函数在处取得极值,则,所以实数的值是2.
(2)因,
令,求导得:
当时,,当时,
即在上单调递增,在上单调递减
因此,当时,
于是得
所以实数的取值范围是.
20.(1)零假设为:设立自习室对提高学生成绩无效.根据列联表中的数据,计算得到
根据小概率值的独立性检验,我们推断不成立,即认为设立自习室对提高学生成绩有效,
此推断犯错误的概率不大于0.001.
(2)易知的所有可能取值为0,1,2.
.
所以的分布列为:
0 1 2
所以
同理可得的所有可能取值为0,1,2,
,
所以的分布列为:
0 1 2
所以,即,
其实际含义是设立自习室后学生的数学成绩提高,说明设立自习室对提高学生成绩有效.
21.(12分)
(1)根据散点图,呈现非线性的变化趋势,故更适合作为关于的回归方程类型.
(2)对两边取对数,得,即
由表中数据得:
则,∴关于的回归方程为,当时,
∴当化肥施用量为27公斤时,粮食亩产量约为810公斤.
(3)依题意,
则有,
;
∴这种化肥的有效率超过的概率约为0.02275.
22.(1)当时,,
∴,由,解得
由,得
∴的单调递增区间为,单调递增区间为.
(2)由恒成立,得
∴,
∵,∴恒成立,
设,∴
设,则
∵,∴在上单调递增,而
∴存在,使,即
∴当时,,此时函数单调递减;
当时,,此时函数单调递增
∴在处有极小值(也是最小值),所以
又由恒成立,即,
∴的最大整数值为3.
数学试题
第Ⅰ卷(选择题共60分)
一、选择题:(本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知集合,则( )
A. B. C. D.
2.已知为复数且(i为虚数单位),则共轭复数的虚部为( )
A.2 B. C. D.
3.已知向量,若,则在上的投影向量的坐标为( )
A. B. C. D.
4.下图展现给我们的是唐代著名诗人杜牧写的《清明》,这首诗不仅意境极好,而且还准确地描述出了清明时节的天气状况,那就是“雨纷纷”,即天气多阴雨.某地区气象监测资料表明,清明节当天下雨的概率是0.9,连续两天下雨的概率是0.63,若该地某年清明节当天下雨,则随后一天也下雨的概率是( )
A.0.63 B.0.7 C.0.9 D.0.567
5.为了得到函数的图象,只需要把函数的图象上( )
A.各点的横坐标缩短到原来的,再向左平移个单位长度
B.各点的横坐标缩短到原来的,再向左平移个单位长度
C.各点的横坐标伸长到原来的倍,再向左平移个单位长度
D.各点的横坐标伸长到原来的2倍,再向左平移个单位长度
6.下列说法中,正确的命题是( )
A.已知随机变量服从正态分布,则
B.线性相关系数越大,两个变量的线性相关性越强,反之,线性相关性越弱
C.已知两个变量具有线性相关关系,其回归方程为,若,则
D.若样本数据的方差为8,则数据的方差为2
7.在三棱锥中,平面,且.若三棱锥的外接球体积为,则当该三棱锥的体积最大时,其表面积为( )
A. B. C. D.
8.设某工厂有两个车间生产同型号家用电器,第一车间的合格率为0.85,第二车间的合格率为0.88,两个车间的成品都混合堆放在一个仓库,假设第一,二车间生产的成品比例为2∶3,今有一客户从成品仓库中随机提一台产品,则该产品合格的概率为( )
A.0.6 B.0.85 C.0.868 D.0.88
二、多项选择题:(本题共4小题,每小题5,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分。)
9.在公比为整数的等比数列中,是数列的前项和,若,则下列说法正确的是( )
A. B.数列是等比数列
C. D.数列是公差为2的等差数列
10.下列说法正确的是( )
A.在一组样本数据的散点图中,若所有样本点都在直线上,则这组数据的样本相关系数为1
B.若变量的样本相关系数为0,则x与不存在相关关系
C.若以模型拟合一组样本数据,设,将样本数据进行相应变换后算得回归直线的方程为,则的估计值分别为和0.5
D.在回归分析中,相关指数的值越大,说明模型拟合的效果越好
11.已知是自然对数的底数,则下列不等关系中不正确的是( )
A. B. C. D.
12.已知函数,则下列结论中正确的有( )
A.必有唯一极值点
B.若,则在上单调递增
C.若,对有恒成立,则
D.若存在,使得成立,则
第Ⅱ卷(共90分)
三、填空题:(本大题共4小题,每小题5分,共20分,)
13.设随机变量,且,则________.
14.已知的展开式中第5项与第7项的二项式系数相等,且展开式的各项系数之和为1024,则展开式中含的项的系数为________.
15.如图所示的五个区域中,中心区域是一幅图画,现要求在其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色且相邻区域所涂颜色不同,则不同的涂色方法种数为________.
16.已知关于的不等式恒成立,则的取值范围为________.
四、解答题:(本大题共6小题,共70分。解答应写出必要的文字说明、证明过程或演算步骤。)
17.(本题10分)已知函数,其中为常数.
(1)当函数的图象在点处的切线的斜率为1时,求的值;
(2)在(1)的条件下,求函数在上的最小值.
18.(本题12分)一个袋子里装有除颜色以外完全相同的白球和黑球共10个.若从中不放回地取球,每次取1个球,在第一次取出黑球的条件下,第二次取出白球的概率为.
(1)求白球和黑球各有多少个;
(2)若有放回地从袋中随机摸出3个球,求恰好摸到2个黑球的概率;
(3)若不放回地从袋中随机摸出2个球,用表示摸出的黑球个数,求的分布列和期望.
19.(本题12分)已知函数,其中
(1)若函数在处取得极值,求实数的值;
(2)若函数在上恒成立,求实数的取值范围.
20.(本题12分)某中学是走读中学,为了让学生更有效率的利用下午放学后的时间,学校在本学期第一次月考后设立了多间自习室,以便让学生在自习室自主学习、完成作业,同时每天派老师轮流值班.在本学期第二次月考后,高一某班数学老师统计了两次考试该班数学成绩优良人数和非优良人数,得到如下列联表:(单位:人)
是否设立自习室 成绩 合计
非优良 优良
未设立自习室 26 14 40
设立自习室 10 30 40
合计 36 44 80
(1)依据小概率值的独立性检验,能否认为设立自习室对提高学生成绩有效?
(2)设从该班第一次月考的所有数学成绩中任取两个,取到成绩优良数为:从该班第二次月考的所有数学成绩中任取两个,取到成绩优良数为,求与的均值并比较大小,请解释所得结论的实际含义.下面的临界值表供参考:
(参考公式:,其中)
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
21.(本题12分)近年来,由于耕地面积的紧张,化肥的施用量呈增加趋势,一方面,化肥的施用对粮食增产增收起到了关键作用,另一方面,也成为环境污染,空气污染,土壤污染的重要来源之一.如何合理地施用化肥,使其最大程度地促进粮食增产,减少对周围环境的污染成为需要解决的重要问题.研究粮食产量与化肥施用量的关系,成为解决上述问题的前提.某研究团队收集了10组化肥施用量和粮食亩产量的数据并对这些数据作了初步处理,得到了如图所示的散点图及一些统计量的值,化肥施用量为x(单位:公斤),粮食亩产量为y(单位:百公斤).
参考数据:
650 91.5 52.5 1478.6 30.5 15 15 46.5
表中.
(1)根据散点图判断与,哪一个适宜作为粮食亩产量关于化肥施用量的回归方程类型(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;并预测化肥施用量为27公斤时,粮食亩产量的值;
(3)经生产技术提高后,该化肥的有效率Z大幅提高,经试验统计得Z大致服从正态分布,那这种化肥的有效率超过的概率约为多少?
附:①对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为:
②若随机变量,则有
;
③取.
22.(本题12分)已知函数.
(1)当时,求函数的单调区间;
(2)当时,求使不等式恒成立的最大整数的值.
龙西北八校联合体2022-2023学年高二下学期期末考试
数学答案
一、选择题(每小题5分,共40分。)
1.C 2.C 3.C 4.B 5.B 6.D 7.C 8.C
二、多项选择题(本题共4小题,每小题5分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分。)
9.ABC 10.ACD 11.AC 12.BD
三、填空题(本题共4个小题,每小题5分,共20分。)
13.21.6 14.45 15.84 16.
17.(1)函数的定义域为,求导得,
因函数的图象在点处的切线的斜率为1,则解得,
所以的值是1.
(2)由(1)得
由,得或
因,则当时,
当时,
因此函数在上单调递减,在上单调递增
所以函数在上的最小值
18.(1)设袋中有黑球个,则白球有个,
设取出黑球为事件,取出白球的事件为,
解得,所以白球有4个,黑球有6个;
(2)由(1)知摸出黑球的概率是
则有放回地从袋中随机摸出3个球,恰好摸到2个黑球的概率为
(3)的可能取值为则
,
的分布列为:
0 1 2
19.(1)依题意,函数的定义域为,求导得:,
因函数在处取得极值,
则有,解得,此时,
当时,,当时,
因此,函数在处取得极值,则,所以实数的值是2.
(2)因,
令,求导得:
当时,,当时,
即在上单调递增,在上单调递减
因此,当时,
于是得
所以实数的取值范围是.
20.(1)零假设为:设立自习室对提高学生成绩无效.根据列联表中的数据,计算得到
根据小概率值的独立性检验,我们推断不成立,即认为设立自习室对提高学生成绩有效,
此推断犯错误的概率不大于0.001.
(2)易知的所有可能取值为0,1,2.
.
所以的分布列为:
0 1 2
所以
同理可得的所有可能取值为0,1,2,
,
所以的分布列为:
0 1 2
所以,即,
其实际含义是设立自习室后学生的数学成绩提高,说明设立自习室对提高学生成绩有效.
21.(12分)
(1)根据散点图,呈现非线性的变化趋势,故更适合作为关于的回归方程类型.
(2)对两边取对数,得,即
由表中数据得:
则,∴关于的回归方程为,当时,
∴当化肥施用量为27公斤时,粮食亩产量约为810公斤.
(3)依题意,
则有,
;
∴这种化肥的有效率超过的概率约为0.02275.
22.(1)当时,,
∴,由,解得
由,得
∴的单调递增区间为,单调递增区间为.
(2)由恒成立,得
∴,
∵,∴恒成立,
设,∴
设,则
∵,∴在上单调递增,而
∴存在,使,即
∴当时,,此时函数单调递减;
当时,,此时函数单调递增
∴在处有极小值(也是最小值),所以
又由恒成立,即,
∴的最大整数值为3.
同课章节目录
