4.1 生活中的立体图形课件

课件30张PPT。4.1 生活中的立体图形第4章 图形的初步认识1.会识别几何体及几何图形；
2.会画出常见的几何图形；
3.正确理解点、线、面是构成几何图形的基本元素，正确
理解点、线、面的关系.生活中你会经常看见很多实物，由下列实物能想象出
你熟悉的几何体吗？
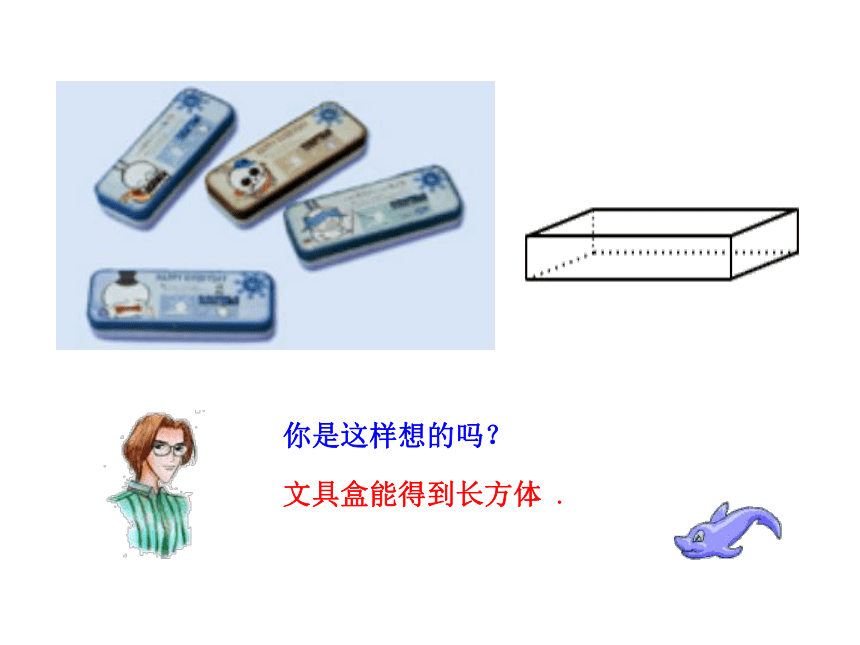
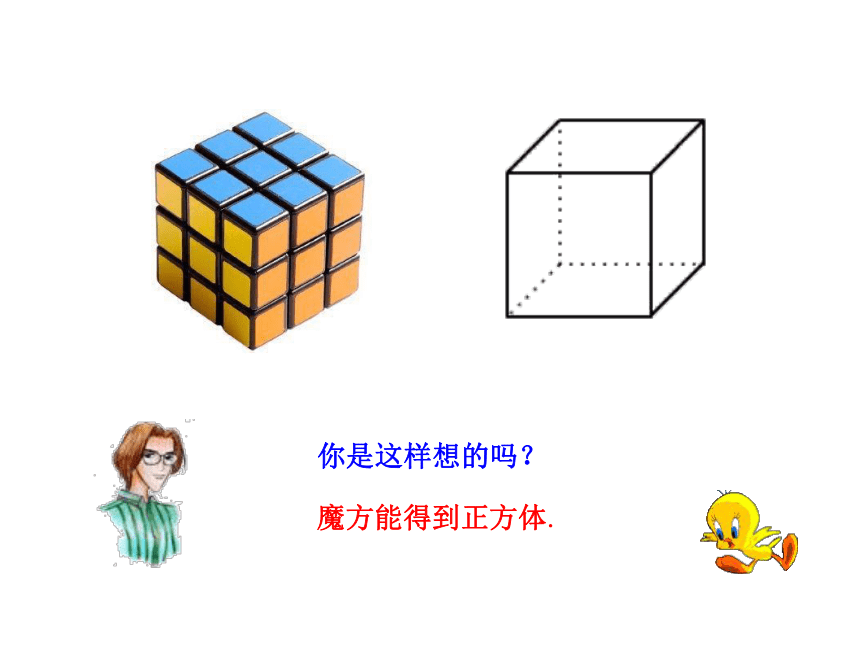
（1）文具盒 （2）魔方 （3）笔筒
（4）足球 （5）漏斗你是这样想的吗？
文具盒能得到长方体 .魔方能得到正方体.你是这样想的吗？笔筒能得到圆柱体. 你是这样想的吗？还有哪些物体形状像圆柱?杯子、茶叶筒、薯片筒、易拉
罐、药瓶等. 圆柱有何特点?上下两个面是 圆，叫底面；侧面是由
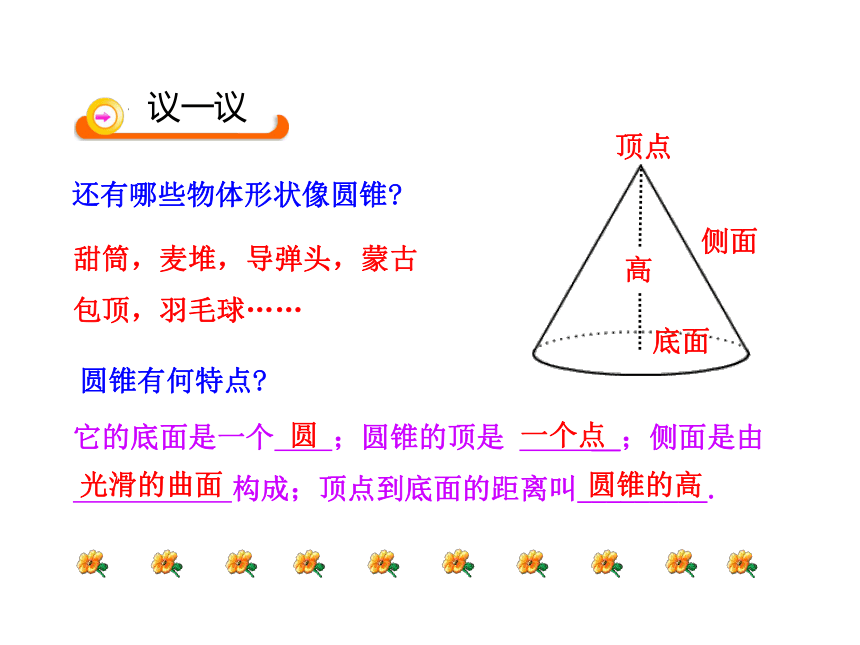
构成；上下两底面之间的距离叫_________. 大小相等的光滑的曲面圆柱的高漏斗能得到圆锥体.你是这样想的吗？还有哪些物体形状像圆锥?圆锥有何特点?甜筒，麦堆，导弹头，蒙古包顶，羽毛球…… 它的底面是一个 ；圆锥的顶是 __；侧面是由
构成；顶点到底面的距离叫_________.圆一个点光滑的曲面圆锥的高底面顶点侧面足球能得到球体.你是这样想的吗？ 通过对你周边物体的观
察、想象，归纳一下我们常
见的几何体有哪些？请你想一想谁来说一说.正方体长方体棱柱圆柱棱锥圆锥球体简单几何体的分类：简单的几何体柱体锥体球体圆柱棱柱圆锥棱锥议一议：柱体有何特点？锥体有何特点？【例1】下列物体的形状类似于球体的是（ ）．
A．茶杯 B．羽毛球 C．乒乓球 D．白炽灯泡
解:选C.根据球体的特征与实物的具体形状进行
判断，可以得到乒乓球的形状类似于球体．
点拨：图形复杂的物体，应去掉非实质的细节干扰，把
它分解为多个基本几何体，化繁为简，再与几何体的特
征进行对照，从而确定此物体是何种几何体． 【例题】1.下面几种图形：①三角形；②长方形；③正方体；
④圆；⑤圆锥；⑥圆柱.其中属于立体图形的是（ ）．
A．③⑤⑥ B．①②③ C．②③⑥ D．④⑤A2.如图所示,是2012年发射神九的火箭．请写出图中含有的两种
立体图形： 、 ． 圆锥 圆柱体 【跟踪训练】1.正方体是由_____面围成的,它们都是_____.
2.正方体有___个顶点，经过每个顶点有___条棱,共
_____条棱.六个平的八三十二2.圆柱的侧面和底面相交成_____条线，它们是_____，是___.1.圆柱是由____个面围成的，其中两个面是_____，一个面是_____. 三平的曲的二曲的圆面有___面和___面；
线有___线和___线.平曲直曲面与面相交得到___；线与线相交得到___.线点...线动成面面动成体点动成线【例2】如图，第二行的图形围绕红线旋转一周，便能形成
第一行的某个几何体，用线连一连.【例题】1.如右图所示，把一个长方形绕着给定的直线旋转一周后，可能形成的几何体是（ ）．【解析】选D.旋转后形成了一个空心的圆柱．【跟踪训练】2.如图所示，各立体图形分别是由几个面围成的？它们是
平的还是曲的．【解析】圆台是由三个面围成的，两个底面是平面，一个
侧面是曲面;正方体是由六个面围成的，每个面都是平的;圆锥由两个面围成，侧面是曲面，底面是平面；图中的棱柱由五个面围成，都是平面．1.（广州·中考）将如图所示的直角梯形绕直线l旋转一
周，得到的立体图形是（ ）．【解析】选C.直角梯形的上底短，下底长，绕直角腰
所在的直线旋转后上底形成的圆小于下底形成的圆，得
到的立体图形是一个圆台．2.直四棱柱，长方体和正方体之间的包含关系是（ ）【解析】选A.根据直四棱柱、长方体、正方体的定义，
可以得到直四棱柱包含长方体，长方体包含正方体．3.从棱长为2的正方体毛坯的一角，挖
去一个棱长为1的小正方体，得到一个
如图所示的零件，则这个零件的表面积
是（ ）．
A．20 B．22 C．24 D．26 【解析】选C.这个零件的表面积就相当于棱长为2的
正方体的表面积，正方体共有6个面，每个面的面积是
4，所以6个面的总面积是24．4.一个正方体的面共有（ ）．
A．1个 B．2个 C．4个 D．6个
【解析】选D.一个正方体由四个侧面和两个底面组
成，共6个面.