4.5 最基本的图形——点和线

课件46张PPT。4.5 最基本的图形——点和线1.在现实情境中理解直线、射线、线段等简单的平面图
形，感受图形世界的丰富多彩.
2.掌握两点间的距离概念,知道“两点之间的所有连线中,
线段最短”,知道“经过两点有一条直线,并且只有一条
直线”.3.能用圆规画一条线段等于已知线段.
4.通过探究活动，积累一定的操作经验，提高条理的思
考与表达能力，培养学生归纳、概括及用语言表达结论
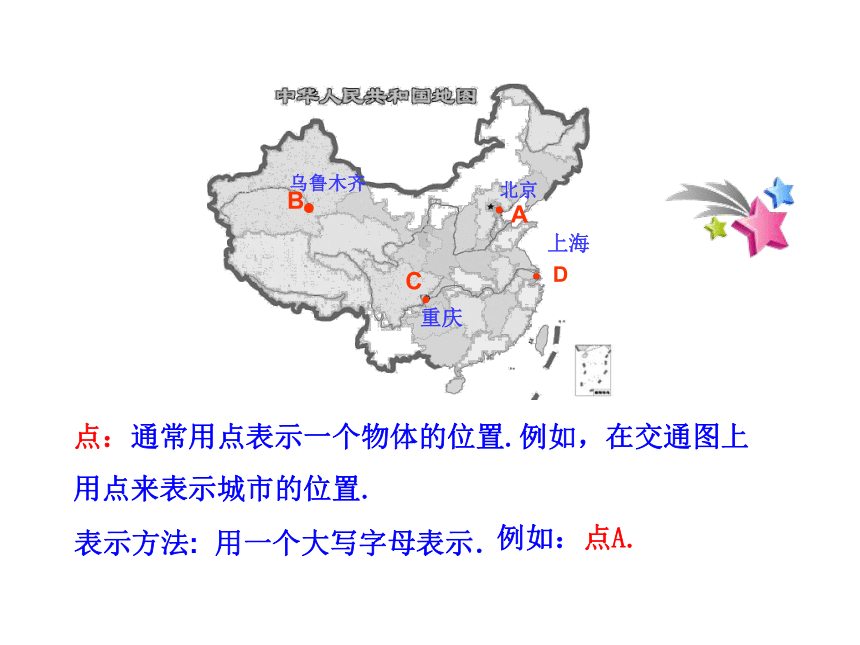
的能力.看一看想一想烛光尖端运动后形成的图形?………………………..拉紧的绳子刻度尺的边缘点：通常用点表示一个物体的位置.例如，在交通图上
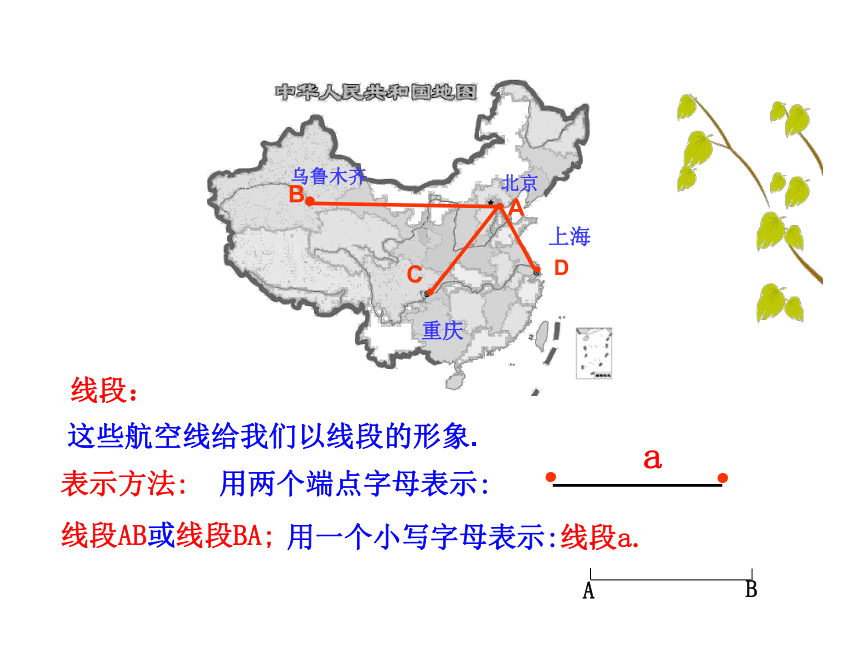
用点来表示城市的位置.　????北京乌鲁木齐上海重庆 ABCD表示方法: 用一个大写字母表示．例如：点A.表示方法: 用两个端点字母表示:
线段AB或线段BA;．这些航空线给我们以线段的形象.线段： 用一个小写字母表示:线段a.a．????北京乌鲁木齐上海重庆 ABCD··O C··O C射线 OC射线 CO射线
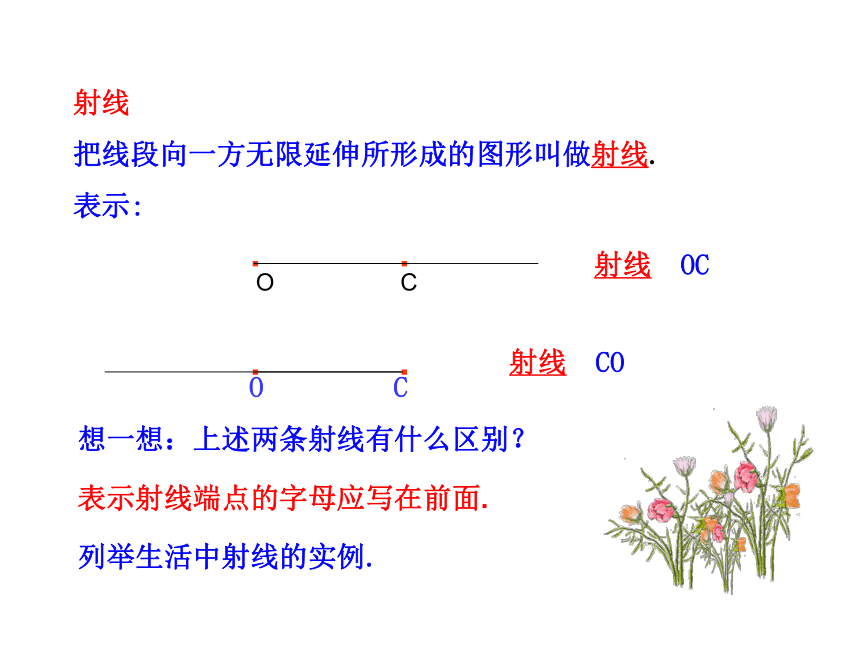
把线段向一方无限延伸所形成的图形叫做射线. 表示:想一想：上述两条射线有什么区别？表示射线端点的字母应写在前面.列举生活中射线的实例.直线
把线段向两方无限延伸所形成的图形叫做直线. 表示:··A B用直线上两个点的大写字母表示:直线 AB 或 BA.用一个小写字母表示:直线 .
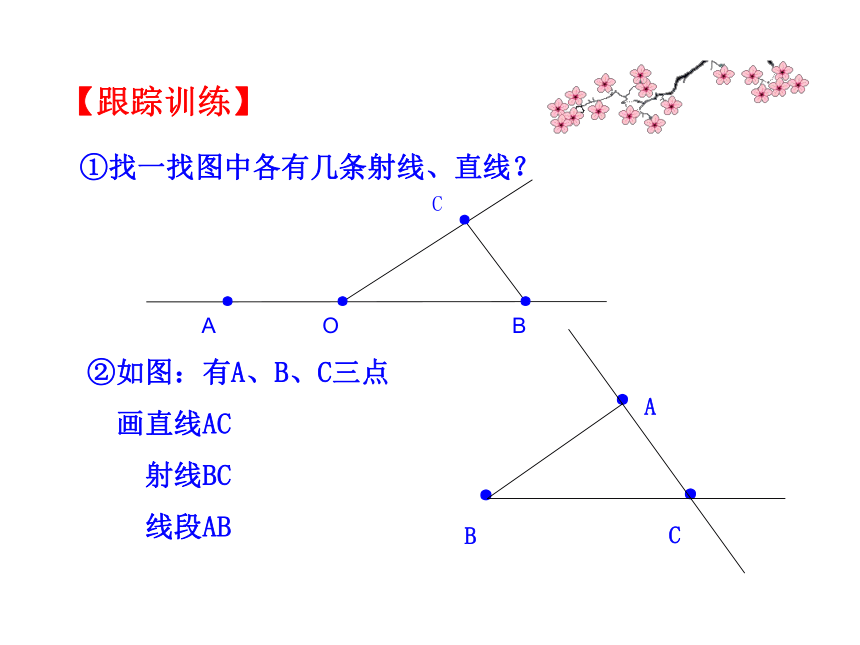
ll①找一找图中各有几条射线、直线？····A O BC②如图：有A、B、C三点
画直线AC
射线BC
线段AB·A·
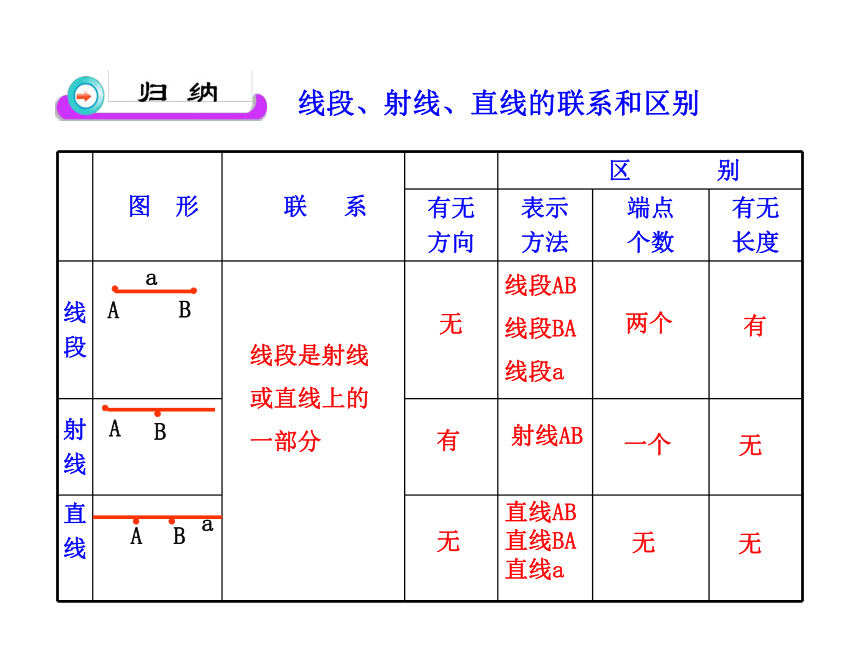
B·C【跟踪训练】A??????ABB无A线段、射线、直线的联系和区别线段AB
线段BA
线段a两个 有射线AB一个无直线AB直线BA
直线a无B线段是射线或直线上的一部分aa无有无从A地到B地有三条路径，你会选择哪一条? 线段AB的长度，就是AB两点间的距离. 两点之间，线段最短.(线段的基本性质)ABC在纸上画一点A和一点B.
边画边思考:(1)过点A能画出几条直线?
(2)经过A,B两点画直线,能画出几条直线?
(3)那么经过三点画直线,能画出几条直线?
[小组讨论] 你们能得出什么结论?结论：
经过一点能画无数条直线，经过两点有一条直线，并且
只有一条直线（两点确定一条直线），经过三点可能画一
条直线，也可能画不出直线.1.下列给线段取名正确的是：( )（A）线段M (B)线段m
（C )线段Mn (D)线段mnB2.如图，若射线AB上有一点C,下列与射线AB是同一条射线的是( )(A)射线BA (B)射线AC
(C)射线BC (D)射线CBA B CB【跟踪训练】 3. 建筑工人在砌墙时，这样拉出的参照线就是直的；木工师傅
用墨盒弹出的墨线也是直的，你能用学过的几何知识来解释他们
这样做的道理吗？经过两点有一条直线，并且只有一条直线.小明家学校（1）（2）（3）(2)两点之间，线段最短4.如图，从小明家到学校共有三条路，小明为了尽快到
学校，应选择第_________条路，用数学知识解释为___________________. 生活中的长短的比较(1) 怎样比较两个同学的高矮?叠合法度量法(2) 怎样比较两根筷子的长短?① 一头对齐，两根棒靠紧， 观察另一头的位置；多出一段的较长.——叠合法.② 用刻度尺分别度量出筷子的长度； 同一长度单位下，数量大的较长.——度量法.注意：在几何里更多的是用前面所说的方法进行比较.　　 画在黑板上的两条线段是无法移动的，在没有度量工具的情况下，请大家想想办法，如何来比较它们的长短？ ② 借助某一物体，如铅笔、小木棒等. 用圆规作一条线段等于已知线段例1.用圆规作一条线段等于已知线段.a① 作射线AB;② 用圆规量出已知线段的长度(记作a);C③ 在射线AB上截取AC = a.比较两条线段的长短：线段AB比线段A1B2长，
即AB>A1B2.线段AB与线段A1B3一样长，即AB=A1B3. baABC 如图，线段c的长度是线段a，b的长度的和，我们就
说线段c是线段a，b的和，记作c=a+b,即AC=AB+BC.类似
的，线段a是线段c与b的差，记作a=c-b，即AB=AC－BC.cABCD如图，在线段AB上，有C，D两点，请完成以下填空：AB=AC+____+____=AD+____=AC+____.CBDBDBCDAC=AD–____=AB–____=AB–____–____.CDDBCBCDCD=AD–____=BC–____=AB–____–____.DBACDBAC【跟踪训练】ABCDM读句画图：(1)画射线AM；(2)射线AM上截取线段AB；(3)再在射线AM上顺次截取BC=CD=AB.试观察图中的线段AB、AC、AD、BC、BD、CD之间有什么
关系？1.观察上图，填空：
AB =（ ）=（ ）；
AC =（ )+( )= 2( )= 2( )；
即AB = BC = （ ）. BCCDABBCBCABAC2.点B具有什么特殊的位置？请你给它起一个名字，并描述
这一位置的特征.
点B把线段AC分成两条相等的线段，点B叫做线段AC的中点.
3.图中还有点B这种特殊位置的点吗？把它找出来.
点C，是线段BD的中点. 把一条线段分成两条相等线段的点,叫做这条线段
的中点.那么线段中点这个定义表达了什么意思呢？我们
来学习用几何符号语言来表示，应从以下两个方面来理
解：AOB1.如图，如果点O把AB分成两条相等线段，即AO=BO，那么点O就是线段AB的中点.这可以用符号语言表示为：如图，点O在线段AB上，因为AO=BO(或AO= AB，或AB=2AO)所以点O是线段AB的中点(线段中点的定义).2.反之，如果已知点O是线段AB的中点，那么就有AO=BO.这可以用符号语言表示为： 如图，因为点O是线段AB的中点 所以AO=BO(或AO= AB，或AB=2AO) (线段中点的定义).BCDMA 观察上图，填空：
AD=_____+______+____=3_____=3_____=3____，
即AB= .ABABBCCDCDBCAD　　点B对于线段AD来说，又具有一个特殊位置，请给
它一个名称，点C具有这一特殊性吗？
　　点B和点C把线段AD分成三条相等的线段，点B叫做
线段AD的一个三等分点.
　　点C也是线段AD的一个三等分点.1.如图，已知线段a，画线段AC＝2a. aABCM线段AC即为所作.【跟踪训练】2.如图，已知线段a，画线段AC= a.a1.量得线段a =12（cm）.=12cm2.计算出 ·a = ×12=4(cm).3.画线段AC = 4(cm)，如下图所示:AC1.画线段使它等于已知线段的和、差、几倍，通常
可用两种不同的方法来画.2.画线段使它等于已知线段的几分之一，通常采用
度量法.(即先量、后算、再画)AONM1.如图所示，下列说法正确的是（ ）
A.直线OM与直线MN是同一直线
B.射线MO与射线MN是同一射线
C.射线OM与射线MN是同一射线
D.射线NO与射线MO是同一射线2.如图,下列说法错误的是（ ）
A.点A在直线m上
B.点A在直线l上
C.点B在直线l上
D.直线m不经过B点BA l mC3.下列说法正确的是（ ）
A.两点确定两条直线
B.三点确定一条直线
C.过一点只能作一条直线
D.过一点可以作无数条直线D4.如图，射线PA与PB是同一条射线，则符合题意的图
为（ ）PABPPPPAAABBBABCDC5.如图所示的直线、射线、线段能相交的是（ ）ABBAAACBBCDCCDDDCABCD6.（柳州·中考）如图，点A，B，C是直线l上的三个点，图中共有线段条数是（ ）
A．1条 B．2条 C．3条 D．4条
【解析】选C.线段AB，AC，BC.7．（嵊州·中考）如图，平面内有公共端点的六条射线OA,OB,OC,OD,OE,OF,从射线OA开始按逆时针方向依次在射线上写出数字1，2，3，4，5，6，7，….则“17”在射线 __________上；“2 007”在射线 上.【解析】17÷6=2…5；2 007÷6=334…3，
所以17在射线OE上，2 007在射线OC上.
答案:OE OC 8.某班同学在操场上站成笔直的一排，确定两个同学的位置,这一排的位置就确定下来了，这是因为________________________________.经过两点有且只有一条直线9.分别用两种方式表示图中的直线直线 AO、直线 BO直线 n、直线 m解：AC=BC= AB=4 cm，
DC= AC=2 cm,EC= CB=2 cm,
DE=DC+CE=2 +2 =4 cm. ABCDE10.如图,线段AB=8 cm，点C是AB的中点，点D是AC的中点，点E是CB的中点，求线段DE的长度.1.直线、射线、线段三者的区别与联系.
2.不同几何语言（文字语言、符号语言、图形语言）的
相互转化.3. 掌握两点间的距离概念,知道“两点之间的所有连线中,线段最短”,知道“经过两点有一条直线,并且只有一条直线”.4.了解线段中点的概念,并能简单运用它来解决问题.