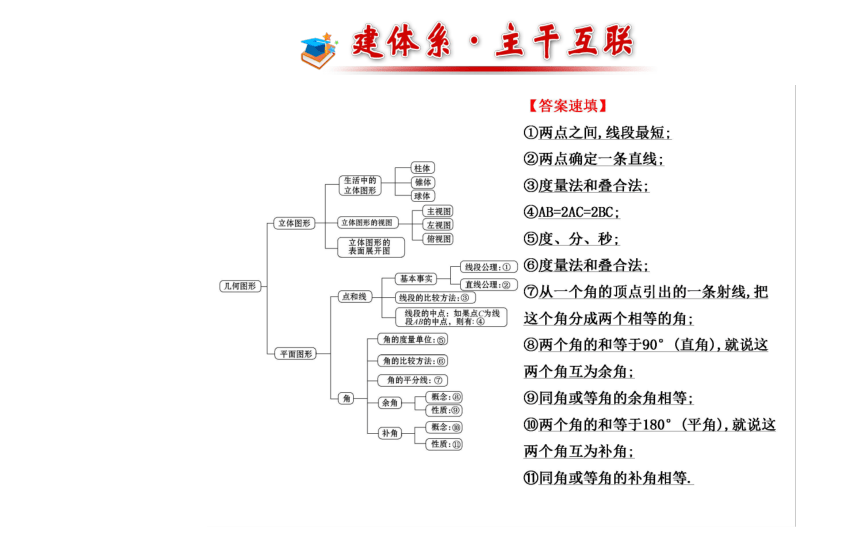
第4章 图形的初步认识阶段复习课

课件44张PPT。阶段复习课
第 4 章主题1 立体图形的视图
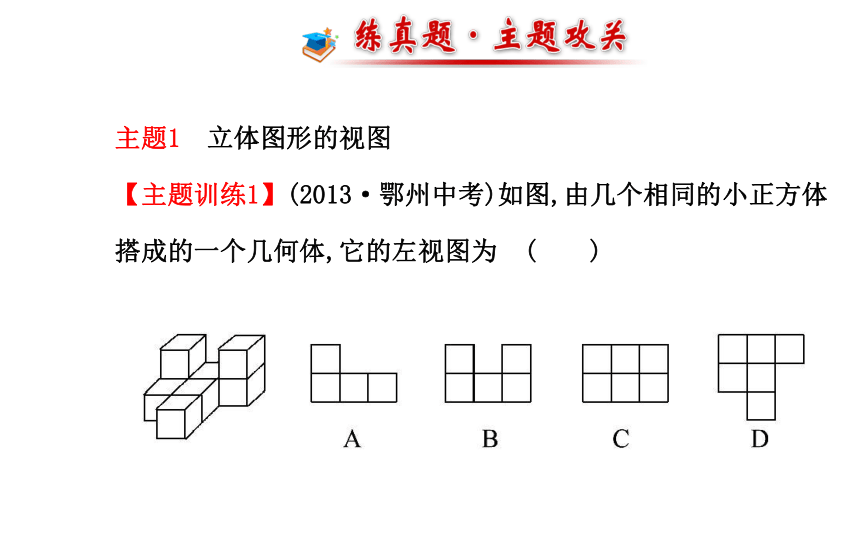
【主题训练1】(2013·鄂州中考)如图,由几个相同的小正方体搭成的一个几何体,它的左视图为　(　　)【自主解答】选A.从几何体左面看,可以看出有三列,左边第一列有两层,第二列、第三列都只有一层.【主题升华】
从不同方向看立体图形
1.从不同方向看立体图形看到的是一个平面图形.
2.画平面图形时,首先确定立体图形的形状,其次考虑它的大小.
3.能够看见的轮廓线用实线,看不见的轮廓线要用虚线表示出来.【备选例题】
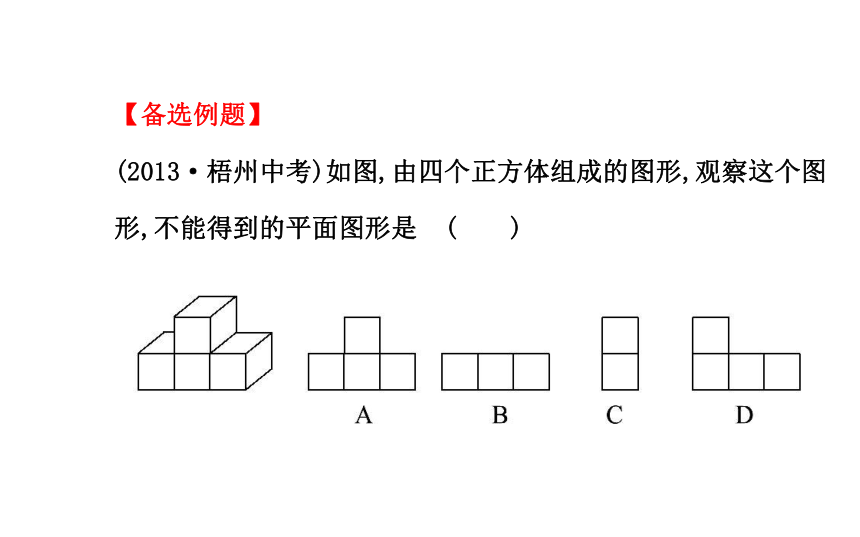
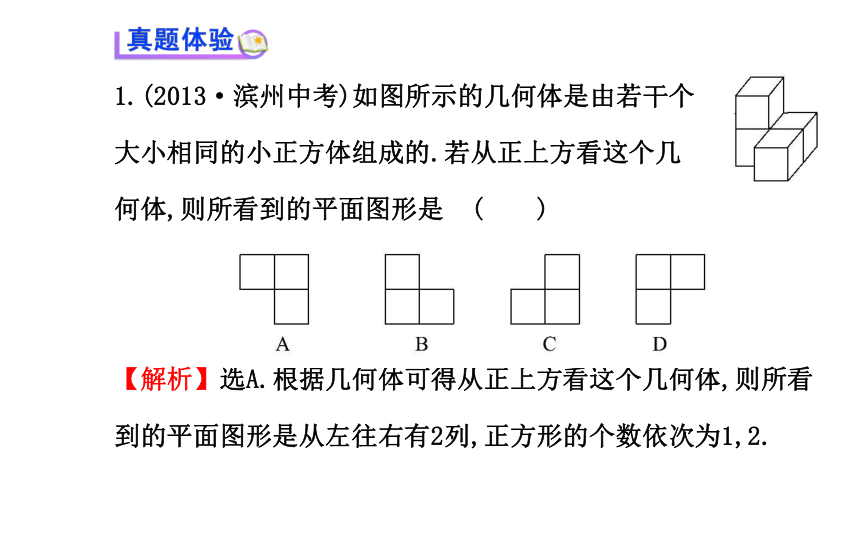
(2013·梧州中考)如图,由四个正方体组成的图形,观察这个图形,不能得到的平面图形是　(　　)【解析】选D.选项A是从正面看到的视图(主视图),选项B是从上面看到的视图(俯视图),选项C是从左面看到的视图(左视图),根据视图中长对正,高平齐,宽相等的性质可还原该物体的几何图形.因此选项D是视图中所看不到的平面图形.1.(2013·滨州中考)如图所示的几何体是由若干个
大小相同的小正方体组成的.若从正上方看这个几
何体,则所看到的平面图形是　(　　)
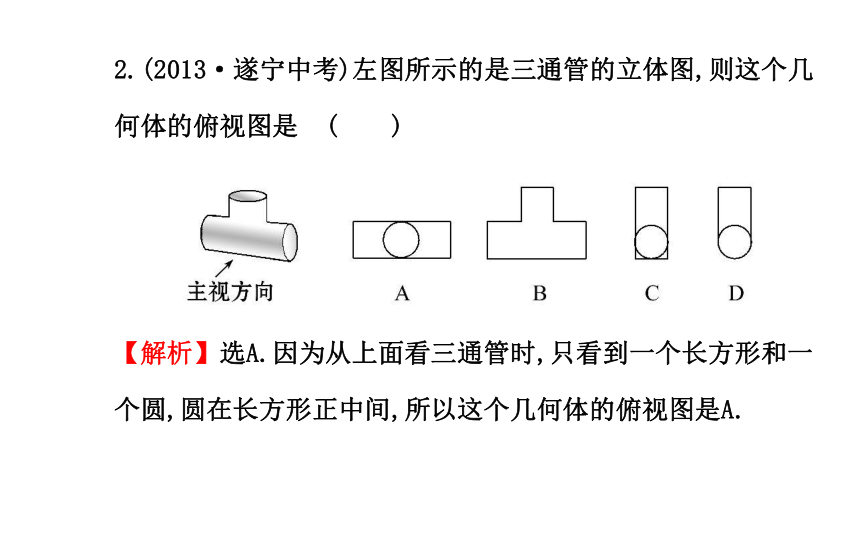
【解析】选A.根据几何体可得从正上方看这个几何体,则所看到的平面图形是从左往右有2列,正方形的个数依次为1,2.2.(2013·遂宁中考)左图所示的是三通管的立体图,则这个几何体的俯视图是　(　　)
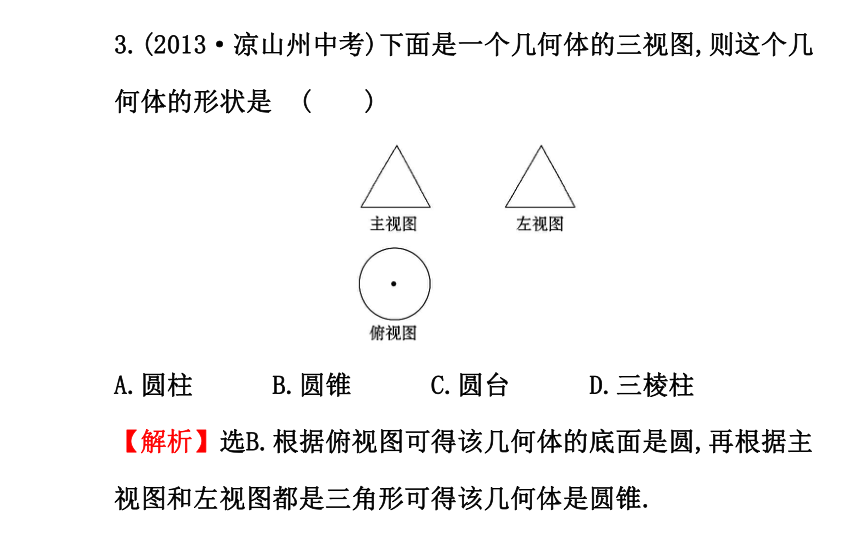
【解析】选A.因为从上面看三通管时,只看到一个长方形和一个圆,圆在长方形正中间,所以这个几何体的俯视图是A.3.(2013·凉山州中考)下面是一个几何体的三视图,则这个几何体的形状是　(　　)
A.圆柱　　　B.圆锥　　　C.圆台　　　D.三棱柱
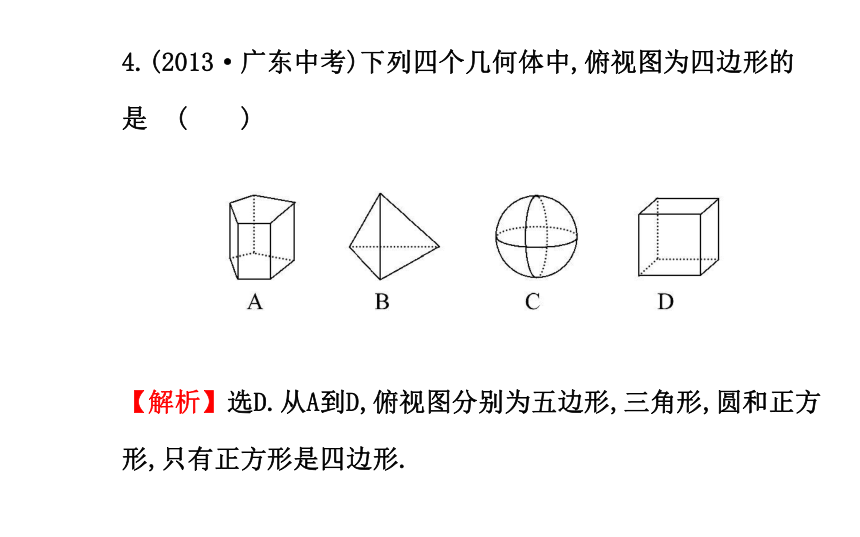
【解析】选B.根据俯视图可得该几何体的底面是圆,再根据主视图和左视图都是三角形可得该几何体是圆锥.4.(2013·广东中考)下列四个几何体中,俯视图为四边形的
是　(　　)
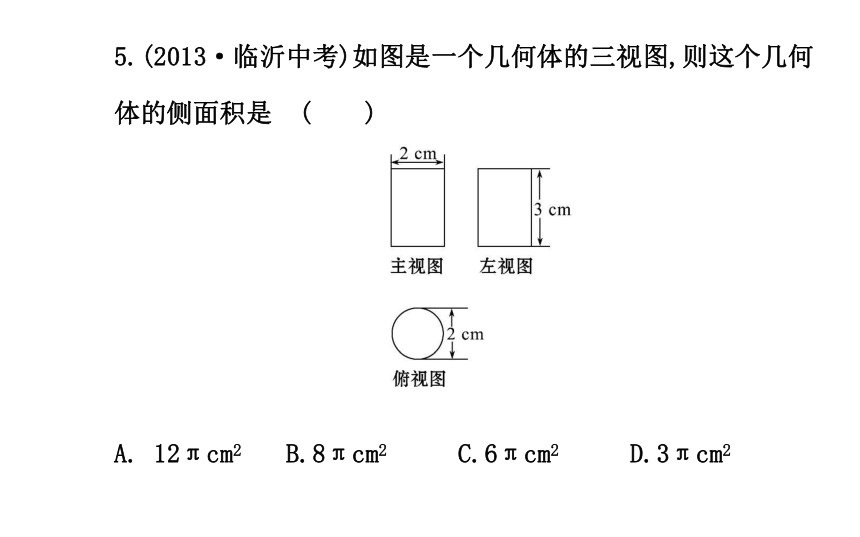
【解析】选D.从A到D,俯视图分别为五边形,三角形,圆和正方形,只有正方形是四边形.5.(2013·临沂中考)如图是一个几何体的三视图,则这个几何体的侧面积是　(　　)
A. 12πcm2 B.8πcm2 C.6πcm2 D.3πcm2【解析】选C.由题意得几何体为圆柱体,圆柱体的侧面展开图为长方形,由三视图得,长方形的长和宽分别为2πcm和3cm,所以圆柱体的侧面积为:3×2π=6πcm2.故选C.主题2 立体图形及其表面展开图
【主题训练2】(2013·巴中中考)如图是一个
正方体的表面展开图,则原正方体中“梦”字
所在的面相对的面上标的字是　(　　)
A.大　　　　B.伟　　　　C.国　　　　D.的
【自主解答】选D.利用正方体及其表面展开图的特点.正方体的表面展开图,共有六个面,其中面“伟”与面“国”相对,面“大”与面“中”相对,面“的”与面“梦”相对.【主题升华】
立体图形的分类及辨别方法
1.基本的立体图形有柱体、锥体、球体.
2.根据立体图形表面形状的不同,柱体可分为圆柱、棱柱,锥体可分为圆锥、棱锥.其中棱柱和棱锥各面都是平面,也叫多面体.3.棱柱和棱锥的命名方法:
(1)可以根据底面的边数,底面是n边形,几何体为n棱柱或n棱锥.
(2)可以根据侧面的棱数,如果有n条,几何体为n棱柱或n棱锥.
(3)可以根据侧面的面数,如果有n个侧面,几何体为n棱柱或n棱锥.
4.这部分内容主要考查学生的空间想象能力,数学概念的形成及立体图形与表面展开图的关系.1.(2013·绵阳中考)把右图中的三棱柱展开,所得到的
展开图是　(　　)
【解析】选B.上、下两底面应在侧面展开图长方形的两侧的只有B,故选B.2.(2013·山西中考)如图是一个长方体包装盒,则它的平面展开图是　(　　)
【解析】选A.根据对面的判断规则只有A选项能找到三组对面,故选A.3.(2013·随州中考)如图是一个长方体形状包装盒的表面展
开图.折叠制作完成后得到长方体的容积是(包装材料厚度不
计)　(　　)
A.40×40×70 　　　B.70×70×80
C.80×80×40 　　　D.40×70×80【解析】选D.长方体的长、宽、高分别为70,40,80,所以长方体的容积为70×40×80.4.(2013·玉溪中考)如图是每个面上都有一个汉字的正方体
的一种平面展开图,那么在原正方体中和“国”字相对的面
是　(　　)
A.中　　　　B.钓　　　　C.鱼　　　　D.岛
【解析】选C.易得“中”相对的面是“的”,“钓”相对的面是“岛”,从而可得“国”相对的面是“鱼”,选C.5.(2013·仙桃中考)小明为了鼓励芦山地震灾区的学生早日走
出阴影,好好学习,制作了一个正方体礼盒(如图).礼盒每个面
上各有一个字,连起来组成“芦山学子加油”,其中“芦”的对
面是“学”,“加”的对面是“油”,则它的平面展开图可能是
　(　　)【解析】选D.A,B,C选项中的“加”和“油”是相邻的面,只有选项D中“加”和“油”是对面,满足题意的是选项D.【变式训练】
(2012·齐齐哈尔中考)小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是　(　　)【解析】选C.根据“预”的对面是“中”,“成”的对面是“功”,得到“祝”的对面是“考”,再根据位于同一行(或同一列),中间隔一个面的两个面一定是相对面,验证各选项,只有C项满足.主题3 直线、射线、线段
【主题训练3】(2012·菏泽中考)已知线段AB=8cm,在直线AB上画线段BC,使BC=3cm,则线段AC=　　　　　　.
【自主解答】由于是在直线AB上画线段BC,BC可能画在线段AB的外部,也可能画在线段AB上,所以AC=AB+BC=8+3=11(cm)或AC=AB-BC=8-3=5(cm).
答案:11cm或5cm【主题升华】
有关“直线、射线、线段”的数学思想
1.数形结合思想:在进行线段的有关计算中,往往结合图形来求解.
2.转化思想:在求立体图形中的最短问题时,一般转化为平面图形中的两点间的问题.
3.分类讨论问题:有关线段的计算时,往往要注意点在线段上或在线段外.【备选例题】
已知线段AB=10cm,直线AB上有一点C,且BC=2cm,点D是线段AB的中点,求线段DC的长.
【解析】(1)当点C在线段AB的外部时,如图1所示.
因为点D是线段AB的中点,所以BD= AB= ×10=5.
所以DC=DB+BC=5+2=7(cm).(2)当点C在线段AB的内部时,如图2所示.
因为点D是线段AB的中点,所以BD= AB= ×10=5.
所以DC=DB-BC=5-2=3(cm).1.(2012·葫芦岛中考)如图,C是线段AB上的一点,M是线段AC的中点,若AB=8 cm,BC=2 cm,则MC的长是　(　　)
A.2 cm　　　B.3 cm　　　C.4 cm　　　D.6 cm【解析】选B.由图可知AC=AB-BC=8-2=6(cm).
因为点M是AC的中点,
所以MC= AC=3 cm.2.(2012·永州中考)永州境内的潇水河畔有朝阳岩、柳子庙和迥龙塔三个名胜古迹(如图所示),其中柳子庙坐落在潇水之西的柳子街上,始建于1056年,是永州人民为纪念唐宋八大家之一的柳宗元而筑建.现有三位游客分别参观这三个景点,为了使这三位游客参观完景点后步行返回旅游车上所走的路程总和最短,那么旅游车等候这三位游客的最佳地点应在　(　　)
A.朝阳岩
B.柳子庙
C.迥龙塔
D.朝阳岩和迥龙塔这段路程的中间位置【解析】选B.用特殊值法.
设朝阳岩距离柳子庙的路程为5,柳子庙距离迥龙塔的路程为8,则迥龙塔距离朝阳岩的路程为13.
A.当旅游车停在朝阳岩时,总路程为5+13=18,
B.当旅游车停在柳子庙时,总路程为5+8=13,
C.当旅游车停在迥龙塔时,总路程为13+8=21,
D.当旅游车停在朝阳岩和迥龙塔这段路程的中间时,总路程大于13,所以路程最短的是旅游车停在柳子庙时.3.(2012·常德中考)若图1中的线段长为1,将此线段三等分,并以中间的一段为边作等边三角形,然后去掉这一段,得到图2,再将图2中的每一段类似变形,得到图3,按上述方法继续下去得到图4,则图4中的折线的总长度为　(　　)
A.2 B. C. D.【解析】选D.第一个线段长=1，
观察发现：第二个图形在第一个图形的长的基础上多了它的长
的 ，
同样，第三个图形在第二个图形的基础上，多了其长的 ，第
四个图形在第三个图形的基础上，多了其长的 .
所以第二个图形的折线的总长度为 ，第三个图形的
折线的总长度为 ；第四个图形的折线的总长度为主题4 角的比较与运算
【主题训练4】(2013·曲靖中考)如图,直线AB,CD相交于点O,若∠BOD =40°,OA平分∠COE,则∠AOE =　　　　　.【自主解答】∠BOD和∠BOC互为补角,∠BOC与∠AOC互为补角,根据同角的补角相等,可得∠AOC=∠BOD =40°,
又OA平分∠COE,所以∠AOE=∠AOC=40°.
答案:40°【主题升华】
角的比较与运算
1.互余、互补反映两角的特殊数量关系.
2.方位角中经常涉及两角的互余.
3.计算两角的和、差时要分清两角的位置关系.1.(2013·厦门中考)已知∠A=60°,则∠A的补角是　(　　)
A.160° B.120° C.60° D.30°
【解析】选B.根据互为补角的两个角之和等于180°,
则180°-60°=120°.2.(2013·湖州中考)把15°30′化成度的形式,则15°30′=
　　　　　度.
【解析】15°30′=15°+ =15.5°.
答案:15.53.(2013·义乌中考)把角度化为度、分的形式,则20.5°=
20°　　′.
【解析】因为1°=60′,所以0.5°=60′×0.5=30′.
答案:304.(2013·泉州中考)如图,∠AOB =90°,∠BOC =30°,则∠AOC =　　　　°.
【解析】因为∠AOB=90°,∠BOC=30°,所以∠AOC =∠AOB -∠BOC=60°.
答案:605.(2013·南宁中考)一副三角板如图所示放置,则∠AOB=
　　　　　°.
【解析】根据三角板的度数可得∠AOB=45°+60°=105°.
答案:105