§18.5实践与探索课件(3)[下学期]
文档属性
| 名称 | §18.5实践与探索课件(3)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 423.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-04 08:50:00 | ||
图片预览




文档简介
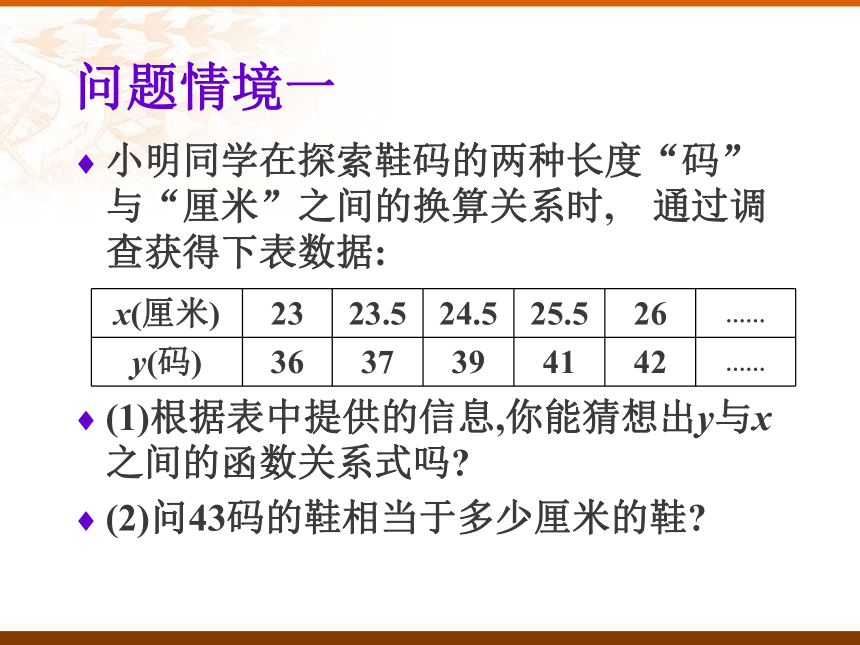
课件13张PPT。§18.5.3实践与探索导言在前几节课里,我们分别学习了一次函数,一次函数的图象,一次函数图象的特征,并且了解到一次函数的应用十分广泛,和我们日常生活密切相关,因此本节课我们一起来学习一次函数图象的应用。 问题情境一小明同学在探索鞋码的两种长度“码”与“厘米”之间的换算关系时,通过调查获得下表数据:
(1)根据表中提供的信息,你能猜想出y与x之间的函数关系式吗?
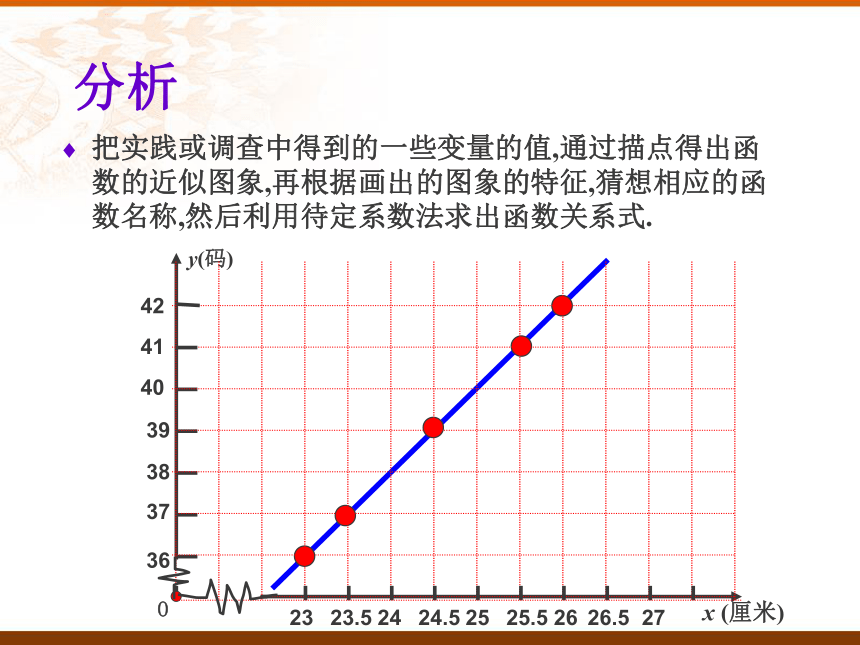
(2)问43码的鞋相当于多少厘米的鞋?分析把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.探究解决方法解:(1)设鞋长是x厘米,鞋子的码数是y,
那么y与x的函数关系式可能是
y=kx+b(k≠0)
根据题意,得所以y与x的函数关系式可能是:y=2x-10(2)当y=43时,2x-10=43,解得x=26.5.问题情境二为了研究某合金材料的体积V(cm3)随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:
你能否据此求出V和t的函数关系? 客观分析分析:将这些数值所对应的点在坐标系中描出.我们发现,这些点大致位于一条直线上,可知V和t近似地符合一次函数关系. 例1 为了学生的身体健康,学校课桌、凳的高度都是按一定的关系科学设计的.小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身长调节高度.于是,他测量了一套课桌、凳上相对应的四档高度,得到如下数据:
(1)小明经过对数据探究,发现:桌高y是凳高x的一次函数,请你求出这个一次函数的关系式(不要求写出x的取值范围);
(2)小明回家后,测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm,请你判断它们是否配套?说明理由 解: (1)设一次函数为y=kx+b(k≠0),将表中数据任取两组,不妨取(37.0,70.0)和(42.0,78.0)代入,得解得一次函数关系式是y=1.6x+10.8.(2)当x=43.5时,y=1.6×43.5+10.8=80.4≠77.答 一次函数关系式是y=1.6x+10.8,小明家里的写字台和凳子不配套 例2 某公司到果园基地购买某种优质水果,慰问医务工作者.果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所买的水果量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)当购买量在什么范围时,选择哪种购买方案付款最少?并说明理由.解 :(1)(2)当,即9x=8x+5000时,解得x=5000.所以当x=5000时,两种付款一样;解得3000≤x<5000.所以当3000≤x<5000时,选择甲方案付款最少;解得x>5000.所以当x>5000时,选择乙方案付款最少.明确两点我们曾采用待定系数法求得一次函数和反比例函数的关系式.但是现实-生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正,建立比较接近的函数关系式进行研究.
常用的方法是:把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.应用提高小明在做电学实验时,电路图如图所示.
在保持电压不变的情况下,改换不同的电阻R,并用电流表测量出通过不同电阻的电流I,记录结果如下:
(1)建立适当的平面直角坐标系,在坐标系中描出表格中的各点,并画出该函数的近似图象;
(2)观察图象,猜想I与R之间的函数关系,并求出函数解析式;
(3)小明将一个未知电阻值的电阻串联到电路中,查得电流表的度数为0.5安培,你知道这个电阻的电阻值吗?解答用描点法画出表格中的各点,可得函数的近似图象(如图所示),由近似图象可知,是反比例函数,且用待定系数法求得函数解析式为I= ,当I=0.5时,R=24.课间练习课本P56的练习
(1)根据表中提供的信息,你能猜想出y与x之间的函数关系式吗?
(2)问43码的鞋相当于多少厘米的鞋?分析把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.探究解决方法解:(1)设鞋长是x厘米,鞋子的码数是y,
那么y与x的函数关系式可能是
y=kx+b(k≠0)
根据题意,得所以y与x的函数关系式可能是:y=2x-10(2)当y=43时,2x-10=43,解得x=26.5.问题情境二为了研究某合金材料的体积V(cm3)随温度t(℃)变化的规律,对一个用这种合金制成的圆球测得相关数据如下:
你能否据此求出V和t的函数关系? 客观分析分析:将这些数值所对应的点在坐标系中描出.我们发现,这些点大致位于一条直线上,可知V和t近似地符合一次函数关系. 例1 为了学生的身体健康,学校课桌、凳的高度都是按一定的关系科学设计的.小明对学校所添置的一批课桌、凳进行观察研究,发现它们可以根据人的身长调节高度.于是,他测量了一套课桌、凳上相对应的四档高度,得到如下数据:
(1)小明经过对数据探究,发现:桌高y是凳高x的一次函数,请你求出这个一次函数的关系式(不要求写出x的取值范围);
(2)小明回家后,测量了家里的写字台和凳子,写字台的高度为77cm,凳子的高度为43.5cm,请你判断它们是否配套?说明理由 解: (1)设一次函数为y=kx+b(k≠0),将表中数据任取两组,不妨取(37.0,70.0)和(42.0,78.0)代入,得解得一次函数关系式是y=1.6x+10.8.(2)当x=43.5时,y=1.6×43.5+10.8=80.4≠77.答 一次函数关系式是y=1.6x+10.8,小明家里的写字台和凳子不配套 例2 某公司到果园基地购买某种优质水果,慰问医务工作者.果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门;乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所买的水果量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)当购买量在什么范围时,选择哪种购买方案付款最少?并说明理由.解 :(1)(2)当,即9x=8x+5000时,解得x=5000.所以当x=5000时,两种付款一样;解得3000≤x<5000.所以当3000≤x<5000时,选择甲方案付款最少;解得x>5000.所以当x>5000时,选择乙方案付款最少.明确两点我们曾采用待定系数法求得一次函数和反比例函数的关系式.但是现实-生活中的数量关系是错综复杂的,在实践中得到一些变量的对应值,有时很难精确地判断它们是什么函数,需要我们根据经验分析,也需要进行近似计算和修正,建立比较接近的函数关系式进行研究.
常用的方法是:把实践或调查中得到的一些变量的值,通过描点得出函数的近似图象,再根据画出的图象的特征,猜想相应的函数名称,然后利用待定系数法求出函数关系式.应用提高小明在做电学实验时,电路图如图所示.
在保持电压不变的情况下,改换不同的电阻R,并用电流表测量出通过不同电阻的电流I,记录结果如下:
(1)建立适当的平面直角坐标系,在坐标系中描出表格中的各点,并画出该函数的近似图象;
(2)观察图象,猜想I与R之间的函数关系,并求出函数解析式;
(3)小明将一个未知电阻值的电阻串联到电路中,查得电流表的度数为0.5安培,你知道这个电阻的电阻值吗?解答用描点法画出表格中的各点,可得函数的近似图象(如图所示),由近似图象可知,是反比例函数,且用待定系数法求得函数解析式为I= ,当I=0.5时,R=24.课间练习课本P56的练习
