黑龙江省齐齐哈尔市龙沙区恒昌中学校2022-2023学年高二下学期期末数学试题(含解析)
文档属性
| 名称 | 黑龙江省齐齐哈尔市龙沙区恒昌中学校2022-2023学年高二下学期期末数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 780.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 23:20:09 | ||
图片预览




文档简介
2022-2023学年度下学期高二学年
期末教学质量检测
数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一.选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则( )
A. B. C. D.
2.设命题:,,则为( )
A., B.,
C., D.,
3.下列有关事件的说法正确的是( )
A.事件,中至少有一个发生的概率一定比,中恰有一个发生的概率大
B.若,则事件,为对立事件
C.若,为互质事件,则
D.若事件,,满足条件,和为互斥事件,则
4.已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡.若顾客甲只用银联卡结账,顾客乙只用微信和银联卡结账,顾客丁与甲、乙结账方式不同,丙用哪种结账方式都可以.若甲乙丙丁购物后依次结账,那么他们结账方式的组合种数共有( )
A.20种 B.24种 C.30种 D.36种
5.设随机变量,且满足,,则( )
A.0.7 B.0.6 C.0.4 D.0.3
6.已知,,,则( )
A. B. C. D.
7.某次考试共有8道单选题,某学生对其中7道题有思路,1道题完全没有思路.有思路的题目每道做对的概率为0.6,没有思路的题目,只好任意猜一个答案,猜对的概率为0.25.若从这8道题中任选2道,则这个学生2道题全做对的概率为( )
A.0.27 B.0.0375 C.0.3075 D.0.3175
8.已知函数的定义域为,值域为,且,,函数的最小值为2,则( )
A. B. C. D.
二、多选题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多个项符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列命题不正确的是( )
A.是的充分不必要条件,
B.,
C.若,则
D.设,为两个集合,若不包含于,则,使得
10.已知是定义在上的奇函数,是定义在上的偶函数,且,在单调递增,则( )
A. B.
C. D.
11.某地区高三女生的“50米跑”测试成绩(单位:秒)服从正态分布,且.从该地区高三女生的“50米跑”测试成绩中随机抽取5个,其中成绩在内的个数记为,则下列说法正确的有( )
A. B.
C. D.
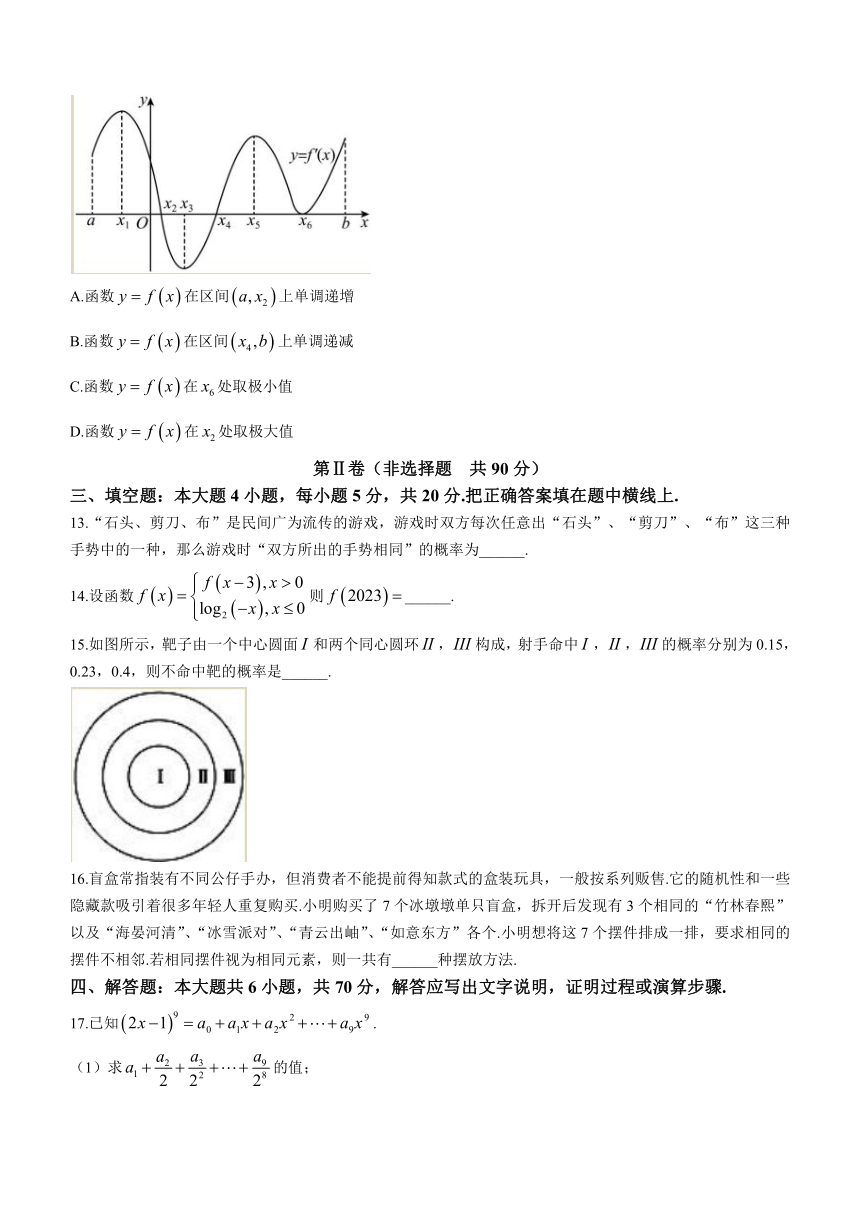
12.如图是导函数的导函数的图像,则下列说法正确的是( )
A.函数在区间上单调递增
B.函数在区间上单调递减
C.函数在处取极小值
D.函数在处取极大值
第Ⅱ卷(非选择题 共90分)
三、填空题:本大题4小题,每小题5分,共20分.把正确答案填在题中横线上.
13.“石头、剪刀、布”是民间广为流传的游戏,游戏时双方每次任意出“石头”、“剪刀”、“布”这三种手势中的一种,那么游戏时“双方所出的手势相同”的概率为______.
14.设函数则______.
15.如图所示,靶子由一个中心圆面和两个同心圆环,构成,射手命中,,的概率分别为0.15,0.23,0.4,则不命中靶的概率是______.
16.盲盒常指装有不同公仔手办,但消费者不能提前得知款式的盒装玩具,一般按系列贩售.它的随机性和一些隐藏款吸引着很多年轻人重复购买.小明购买了7个冰墩墩单只盲盒,拆开后发现有3个相同的“竹林春熙”以及“海晏河清”、“冰雪派对”、“青云出岫”、“如意东方”各个.小明想将这7个摆件排成一排,要求相同的摆件不相邻.若相同摆件视为相同元素,则一共有______种摆放方法.
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17.已知.
(1)求的值;
(2)求的值.
18.作为一种益智游戏,中国象棋具有悠久的历史,中国象棋的背后,体现的是博大精深的中华文化.为了推广中国象棋,某地举办了一次地区性的中国象棋比赛,李夏作为选手参加.除李夏以外的其他参赛选手中,是一类棋手,是二类棋手,其余的是三类棋手.
李夏与一、三、三类棋手比赛获胜的概率分别是0.2、0.4和0.5.
(1)从参赛选手中随机选取一位棋手与李夏比赛,求李夏获胜的概率;
(2)如果李夏获胜,求与李夏比赛的棋手为一类棋手的概率.
19.已知函数.
(1)若在处的切线方程为,求实数,的值;
(2)记,若在时有极值0,求实数,的值.
20.近几年我国新能源汽车产业发展迅速.下表是某省新能源汽车的年销售量与年份的统计表:
年份 2018 2019 2020 2021 2022
年销售量(万台) 13 22 25 20 40
某机构调查了该省200位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油汽车 购置新能源汽车 总计
男性车主 30 150
女性车主 30
总计 200
(1)求新能源汽车的销售量关于年份的样本相关系数,并推断与的相关程度;
(2)请将上述列联表补充完整,并根据小概率值的独立性检验,判断购车车主购置新能源汽车是否与性别有关.
参考公式:相关系数,
卡方统计量,其中.
参考数据:,若,则可判断与相关程度很强.
附表:
0.15 0.10 0.05 0.025 0.010 0.005
2.072 2.706 3.841 5.024 6.635 7.879
21.据世界田联官方网站消息,原定于2023年5月13、14日在中国广州举办的世界田联接力赛延期至2025年4月至5月举行.据了解,甲、乙、丙三支队伍将会参加2025年4月至5月在广州举行的米接力的角逐.接力赛分为预赛、半决赛和决赛,只有预赛、半决赛都获胜才能进入决赛.已知甲队在预赛和半决赛中获胜的概率分别为和;乙队在预赛和半决赛中获胜的概率分别为和;丙队在预赛和半决赛中获胜的概率分别为和.
(1)甲、乙、丙三队中,谁进入决赛的可能性最大;
(2)设甲、乙、丙三队中进入决赛的队伍数为,求的分布列.
22.已知函数,其中为实数.
(1)若,求函数的最小值.
(2)若方程有两个实数解,求证:.
2022-2023 学年下学期高二数学期末答案
一、选择题(每小题5分,共8小题40分)
1.【答案】B
【解析】集合,而,
所以.故选:B.
2.【答案】D
【解析】存在量词命题的否定为全称量词命题,故选:D.
3.【答案】C
【解析】对于A,若事件和都为不可能事件.所以A错误;对于B,若在不同试验下,虽然有,但事件和不对立.若在同一试验下,说明事件和对立,则B错误;对于C,,互斥,若,对立,则,若,不对立,则,C正确;若事件,,满足条件,和为互斥事件,则,则D错误,故选:C.
4.【答案】A
【解析】当乙用银联卡结算时,此时甲和乙都用银联卡结算,所以丁有3种方法,丙有4种方法,共有种方法;当乙用微信结算时,此时甲用银联卡结算,丁有2种方法,丙有4种方法,共有种方法,综上,共有种方法.故选:A
5.【答案】A
【解析】依题意可知,,即,
解得或.
又,所以,所以,解得.
所以.故选:A.
6.【答案】B
【解析】因为,,,
由,所以,由,而,则,所以,综上:,故选:B
7.【答案】C
【解析】设事件表示“两道题全做对”,若两个题目都有思路,则,若两个题目中一个有思路一个没有思路,则,故,故选:C.
8.【答案】D
【解析】方法一
令,有,则满足.
又因为,
所以,
因为,
所以,
所以,
所以.
方法二:抽象出特殊函数,其满足题目要求,从而快速求得答案
故选:D.
二、多选题(每小题5分,共4小题20分)
9.【答案】AC
【解析】由可知或,所以是的必要不充分条件,所以A不正确;当时,,所以B正确;若,则,不正确,例如,,所以C不正确;由集合间的基本关系可知,D正确;故选:AC.
10.【答案】BC
【解析】因为是定义在上的奇函数,是定义在上的偶函数,且两函数在上单调递增,所以在上单调递增在上单调递减,在上单调递增,所以,,所以,,,所以BC正确,A错误;若,则,D错误.故选:BC
11.【答案】ACD
【解析】A.因为,,正态分布密度曲线的对称轴为,
根据对称性可知,,,故A正确;
B.,,
所以,故B错误;
C.,,故C正确;
D.,,
,故D正确.
故选:ACD.
12.【答案】AD
【解析】由图像可知,当时,,则函数单调递增,
当时,,则函数单调递减,
所以当时,函数有极大值,故A,D正确,
当时,,则函数单调递增,故B错误;
当时,,则函数单调递增,
当时,,则函数单调递增,
所以不是函数的极值点,故错误.
故选:AD.
三、填空题(每小题5分,共4小题20分)
13.【答案】
【解析】游戏时,双方所出的手势共有种;其中“双方所出的手势相同”有3种;∴“双方所出的手势相同”的概率.
14.【答案】1
【解析】由.故答案为:1.
15.【答案】0.22
【解析】故射手不中靶的概率为,
16.【答案】240
【解析】记3个相同的“竹林春熙”为,“海晏河清”为,“冰雪派对”为,“青云出岫”为,“如意东方”为,先摆放,,,一共有种摆放方式,再将3个插空放入,有种摆放方式,所以,一共有种摆放方式.
四、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)
17.【答案】见解析
【解析】(1)令,可得.
令,可得.
所以,所以,
(2)因为,
则.
令,则
18.【答案】见解析
【解析】(1)设“李夏与第类棋手相遇”,根据题意,,,记“李夏获胜”,则有,,由全概率公式,
李夏在比赛中获胜的概率为.
所以李夏获胜的概率为0.35.
(2)李夏获胜时,则与李夏比赛的棋手为一类棋手的概率为
.
即李夏获胜,对手为一类棋手的概率为.
19.【答案】见解析
【解析】(1)函数,求导得,
因在处的切线方程为,
则,解得,
所以,.
(2)依题意,,求导得,
因在时有极值0,
则,解得或,
当,时,,
当时,,当时,,
则函数在时有极值0,所以,
当,时,,
当时,,当时,,
则函数在时有极值0,所以,,.
综上,符合题意的,的值为或
20.【答案】见解析
【解析】(1)依题意,.
故,
,,
则
故与相关程度很强.
(2)列联表如下:
购置传统燃油汽车 购置新能源汽车 总计
男性车主 120 30 150
女性车主 30 20 50
总计 150 50 200
零假设:购车车主是否购置新能源乘用车与性别无关.
根据列联表中的数据,可得,
根据小概率值的独立性检验,我们推断不成立,
即认为购车车主是否购置新能源乘用车与性别有关,此推断犯错误的概率不超过0.05.
21.【答案】见解析
【解析】(1)甲队进入决赛的概率为,
乙队进入决赛的概率为,
丙队进入决赛的概率为,
显然甲队进入决赛的概率最大,所以甲进入决赛的可能性最大
(2)由(1)可知:甲、乙、丙三队进入决赛的概率分别为,,,
的可能取值为0,1,2,3,
,
,
,
所以的分布列为:
0 1 2 3
22.【答案】见解析
【解析】(1)当时,,则,
由得,
∴当时,;当时,
∴在上单调递减,在上单调递增,
∴
(2)证明:方法1:由题意得,令,
两式相除得,变形得
欲证,即证,即证.
记,
故在上单调递减,
从而,即,所以得证.
方法2:由题意得:
由(1)可知,令,则,则,
两式相除得,,,
欲证,即证,即证.
记,
令,
故在上单调递减,则,
即,∴在上单调递减,从而,
∴得证,
即得证.
期末教学质量检测
数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一.选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合,,则( )
A. B. C. D.
2.设命题:,,则为( )
A., B.,
C., D.,
3.下列有关事件的说法正确的是( )
A.事件,中至少有一个发生的概率一定比,中恰有一个发生的概率大
B.若,则事件,为对立事件
C.若,为互质事件,则
D.若事件,,满足条件,和为互斥事件,则
4.已知某超市为顾客提供四种结账方式:现金、支付宝、微信、银联卡.若顾客甲只用银联卡结账,顾客乙只用微信和银联卡结账,顾客丁与甲、乙结账方式不同,丙用哪种结账方式都可以.若甲乙丙丁购物后依次结账,那么他们结账方式的组合种数共有( )
A.20种 B.24种 C.30种 D.36种
5.设随机变量,且满足,,则( )
A.0.7 B.0.6 C.0.4 D.0.3
6.已知,,,则( )
A. B. C. D.
7.某次考试共有8道单选题,某学生对其中7道题有思路,1道题完全没有思路.有思路的题目每道做对的概率为0.6,没有思路的题目,只好任意猜一个答案,猜对的概率为0.25.若从这8道题中任选2道,则这个学生2道题全做对的概率为( )
A.0.27 B.0.0375 C.0.3075 D.0.3175
8.已知函数的定义域为,值域为,且,,函数的最小值为2,则( )
A. B. C. D.
二、多选题:本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多个项符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分.
9.下列命题不正确的是( )
A.是的充分不必要条件,
B.,
C.若,则
D.设,为两个集合,若不包含于,则,使得
10.已知是定义在上的奇函数,是定义在上的偶函数,且,在单调递增,则( )
A. B.
C. D.
11.某地区高三女生的“50米跑”测试成绩(单位:秒)服从正态分布,且.从该地区高三女生的“50米跑”测试成绩中随机抽取5个,其中成绩在内的个数记为,则下列说法正确的有( )
A. B.
C. D.
12.如图是导函数的导函数的图像,则下列说法正确的是( )
A.函数在区间上单调递增
B.函数在区间上单调递减
C.函数在处取极小值
D.函数在处取极大值
第Ⅱ卷(非选择题 共90分)
三、填空题:本大题4小题,每小题5分,共20分.把正确答案填在题中横线上.
13.“石头、剪刀、布”是民间广为流传的游戏,游戏时双方每次任意出“石头”、“剪刀”、“布”这三种手势中的一种,那么游戏时“双方所出的手势相同”的概率为______.
14.设函数则______.
15.如图所示,靶子由一个中心圆面和两个同心圆环,构成,射手命中,,的概率分别为0.15,0.23,0.4,则不命中靶的概率是______.
16.盲盒常指装有不同公仔手办,但消费者不能提前得知款式的盒装玩具,一般按系列贩售.它的随机性和一些隐藏款吸引着很多年轻人重复购买.小明购买了7个冰墩墩单只盲盒,拆开后发现有3个相同的“竹林春熙”以及“海晏河清”、“冰雪派对”、“青云出岫”、“如意东方”各个.小明想将这7个摆件排成一排,要求相同的摆件不相邻.若相同摆件视为相同元素,则一共有______种摆放方法.
四、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17.已知.
(1)求的值;
(2)求的值.
18.作为一种益智游戏,中国象棋具有悠久的历史,中国象棋的背后,体现的是博大精深的中华文化.为了推广中国象棋,某地举办了一次地区性的中国象棋比赛,李夏作为选手参加.除李夏以外的其他参赛选手中,是一类棋手,是二类棋手,其余的是三类棋手.
李夏与一、三、三类棋手比赛获胜的概率分别是0.2、0.4和0.5.
(1)从参赛选手中随机选取一位棋手与李夏比赛,求李夏获胜的概率;
(2)如果李夏获胜,求与李夏比赛的棋手为一类棋手的概率.
19.已知函数.
(1)若在处的切线方程为,求实数,的值;
(2)记,若在时有极值0,求实数,的值.
20.近几年我国新能源汽车产业发展迅速.下表是某省新能源汽车的年销售量与年份的统计表:
年份 2018 2019 2020 2021 2022
年销售量(万台) 13 22 25 20 40
某机构调查了该省200位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油汽车 购置新能源汽车 总计
男性车主 30 150
女性车主 30
总计 200
(1)求新能源汽车的销售量关于年份的样本相关系数,并推断与的相关程度;
(2)请将上述列联表补充完整,并根据小概率值的独立性检验,判断购车车主购置新能源汽车是否与性别有关.
参考公式:相关系数,
卡方统计量,其中.
参考数据:,若,则可判断与相关程度很强.
附表:
0.15 0.10 0.05 0.025 0.010 0.005
2.072 2.706 3.841 5.024 6.635 7.879
21.据世界田联官方网站消息,原定于2023年5月13、14日在中国广州举办的世界田联接力赛延期至2025年4月至5月举行.据了解,甲、乙、丙三支队伍将会参加2025年4月至5月在广州举行的米接力的角逐.接力赛分为预赛、半决赛和决赛,只有预赛、半决赛都获胜才能进入决赛.已知甲队在预赛和半决赛中获胜的概率分别为和;乙队在预赛和半决赛中获胜的概率分别为和;丙队在预赛和半决赛中获胜的概率分别为和.
(1)甲、乙、丙三队中,谁进入决赛的可能性最大;
(2)设甲、乙、丙三队中进入决赛的队伍数为,求的分布列.
22.已知函数,其中为实数.
(1)若,求函数的最小值.
(2)若方程有两个实数解,求证:.
2022-2023 学年下学期高二数学期末答案
一、选择题(每小题5分,共8小题40分)
1.【答案】B
【解析】集合,而,
所以.故选:B.
2.【答案】D
【解析】存在量词命题的否定为全称量词命题,故选:D.
3.【答案】C
【解析】对于A,若事件和都为不可能事件.所以A错误;对于B,若在不同试验下,虽然有,但事件和不对立.若在同一试验下,说明事件和对立,则B错误;对于C,,互斥,若,对立,则,若,不对立,则,C正确;若事件,,满足条件,和为互斥事件,则,则D错误,故选:C.
4.【答案】A
【解析】当乙用银联卡结算时,此时甲和乙都用银联卡结算,所以丁有3种方法,丙有4种方法,共有种方法;当乙用微信结算时,此时甲用银联卡结算,丁有2种方法,丙有4种方法,共有种方法,综上,共有种方法.故选:A
5.【答案】A
【解析】依题意可知,,即,
解得或.
又,所以,所以,解得.
所以.故选:A.
6.【答案】B
【解析】因为,,,
由,所以,由,而,则,所以,综上:,故选:B
7.【答案】C
【解析】设事件表示“两道题全做对”,若两个题目都有思路,则,若两个题目中一个有思路一个没有思路,则,故,故选:C.
8.【答案】D
【解析】方法一
令,有,则满足.
又因为,
所以,
因为,
所以,
所以,
所以.
方法二:抽象出特殊函数,其满足题目要求,从而快速求得答案
故选:D.
二、多选题(每小题5分,共4小题20分)
9.【答案】AC
【解析】由可知或,所以是的必要不充分条件,所以A不正确;当时,,所以B正确;若,则,不正确,例如,,所以C不正确;由集合间的基本关系可知,D正确;故选:AC.
10.【答案】BC
【解析】因为是定义在上的奇函数,是定义在上的偶函数,且两函数在上单调递增,所以在上单调递增在上单调递减,在上单调递增,所以,,所以,,,所以BC正确,A错误;若,则,D错误.故选:BC
11.【答案】ACD
【解析】A.因为,,正态分布密度曲线的对称轴为,
根据对称性可知,,,故A正确;
B.,,
所以,故B错误;
C.,,故C正确;
D.,,
,故D正确.
故选:ACD.
12.【答案】AD
【解析】由图像可知,当时,,则函数单调递增,
当时,,则函数单调递减,
所以当时,函数有极大值,故A,D正确,
当时,,则函数单调递增,故B错误;
当时,,则函数单调递增,
当时,,则函数单调递增,
所以不是函数的极值点,故错误.
故选:AD.
三、填空题(每小题5分,共4小题20分)
13.【答案】
【解析】游戏时,双方所出的手势共有种;其中“双方所出的手势相同”有3种;∴“双方所出的手势相同”的概率.
14.【答案】1
【解析】由.故答案为:1.
15.【答案】0.22
【解析】故射手不中靶的概率为,
16.【答案】240
【解析】记3个相同的“竹林春熙”为,“海晏河清”为,“冰雪派对”为,“青云出岫”为,“如意东方”为,先摆放,,,一共有种摆放方式,再将3个插空放入,有种摆放方式,所以,一共有种摆放方式.
四、解答题(第17题10分,第18题12分,第19题12分,第20题12分,第21题12分,第22题12分,共6小题70分)
17.【答案】见解析
【解析】(1)令,可得.
令,可得.
所以,所以,
(2)因为,
则.
令,则
18.【答案】见解析
【解析】(1)设“李夏与第类棋手相遇”,根据题意,,,记“李夏获胜”,则有,,由全概率公式,
李夏在比赛中获胜的概率为.
所以李夏获胜的概率为0.35.
(2)李夏获胜时,则与李夏比赛的棋手为一类棋手的概率为
.
即李夏获胜,对手为一类棋手的概率为.
19.【答案】见解析
【解析】(1)函数,求导得,
因在处的切线方程为,
则,解得,
所以,.
(2)依题意,,求导得,
因在时有极值0,
则,解得或,
当,时,,
当时,,当时,,
则函数在时有极值0,所以,
当,时,,
当时,,当时,,
则函数在时有极值0,所以,,.
综上,符合题意的,的值为或
20.【答案】见解析
【解析】(1)依题意,.
故,
,,
则
故与相关程度很强.
(2)列联表如下:
购置传统燃油汽车 购置新能源汽车 总计
男性车主 120 30 150
女性车主 30 20 50
总计 150 50 200
零假设:购车车主是否购置新能源乘用车与性别无关.
根据列联表中的数据,可得,
根据小概率值的独立性检验,我们推断不成立,
即认为购车车主是否购置新能源乘用车与性别有关,此推断犯错误的概率不超过0.05.
21.【答案】见解析
【解析】(1)甲队进入决赛的概率为,
乙队进入决赛的概率为,
丙队进入决赛的概率为,
显然甲队进入决赛的概率最大,所以甲进入决赛的可能性最大
(2)由(1)可知:甲、乙、丙三队进入决赛的概率分别为,,,
的可能取值为0,1,2,3,
,
,
,
所以的分布列为:
0 1 2 3
22.【答案】见解析
【解析】(1)当时,,则,
由得,
∴当时,;当时,
∴在上单调递减,在上单调递增,
∴
(2)证明:方法1:由题意得,令,
两式相除得,变形得
欲证,即证,即证.
记,
故在上单调递减,
从而,即,所以得证.
方法2:由题意得:
由(1)可知,令,则,则,
两式相除得,,,
欲证,即证,即证.
记,
令,
故在上单调递减,则,
即,∴在上单调递减,从而,
∴得证,
即得证.
同课章节目录
