第5章 相交线与平行线阶段复习课

课件21张PPT。阶段复习课
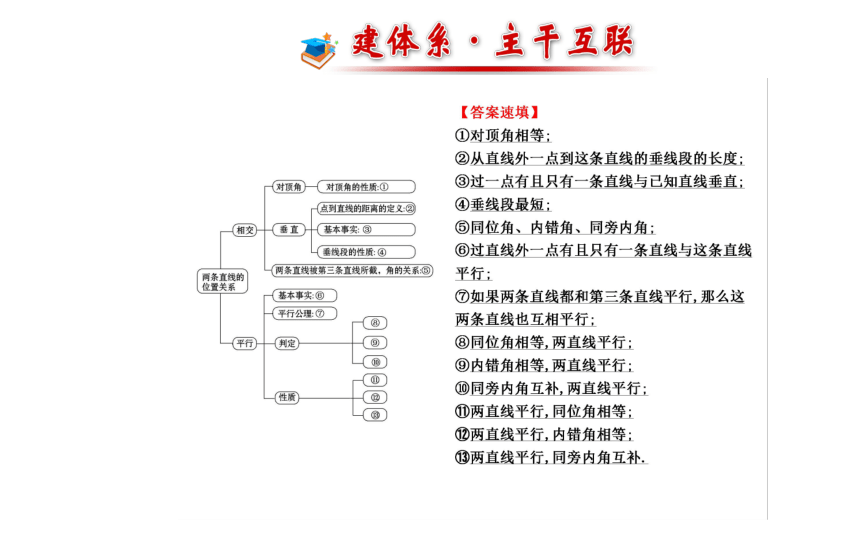
第 5 章主题1 相交线构成的角
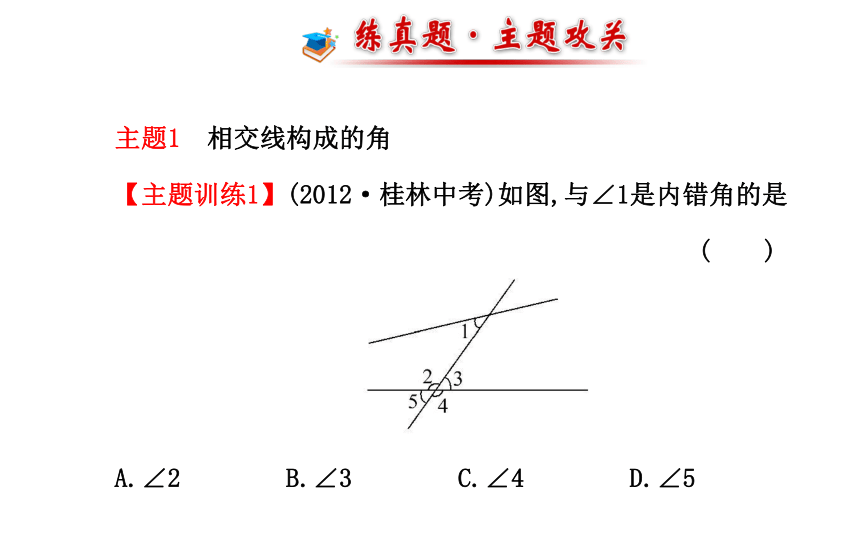
【主题训练1】(2012·桂林中考)如图,与∠1是内错角的是
　(　　)
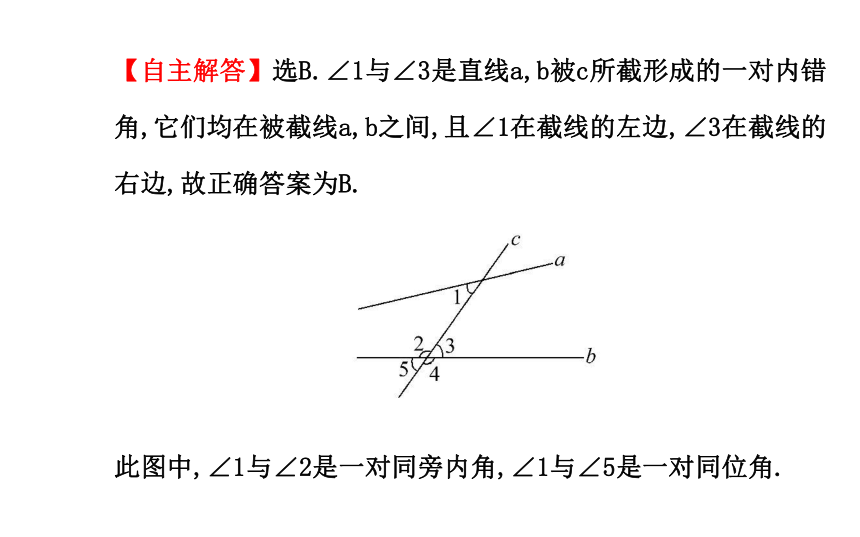
A.∠2　　　　B.∠3　　　　C.∠4　　　　D.∠5【自主解答】选B.∠1与∠3是直线a,b被c所截形成的一对内错角,它们均在被截线a,b之间,且∠1在截线的左边,∠3在截线的右边,故正确答案为B.
此图中,∠1与∠2是一对同旁内角,∠1与∠5是一对同位角.【主题升华】
理解对顶角的“三点注意”
1.判定两个角是不是对顶角,要看这两个角是不是有公共的顶点,两个角的两边是否互为反向延长线,符合这两个条件时,才能判定这两个角是对顶角.
2.对顶角是成对出现的,是具有特殊位置关系的两个角.
3.两条直线相交所成的四个角中共有两对对顶角.1.(2012·北京中考)如图,直线AB,CD交于点O,
射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于
(　　)
A.38° B.104° C.142° D.144°
【解析】选C.因为∠BOD=76°,所以∠AOC=∠BOD=76°,因为射
线OM平分∠AOC,所以∠AOM= ∠AOC= ×76°=38°,所以∠BOM
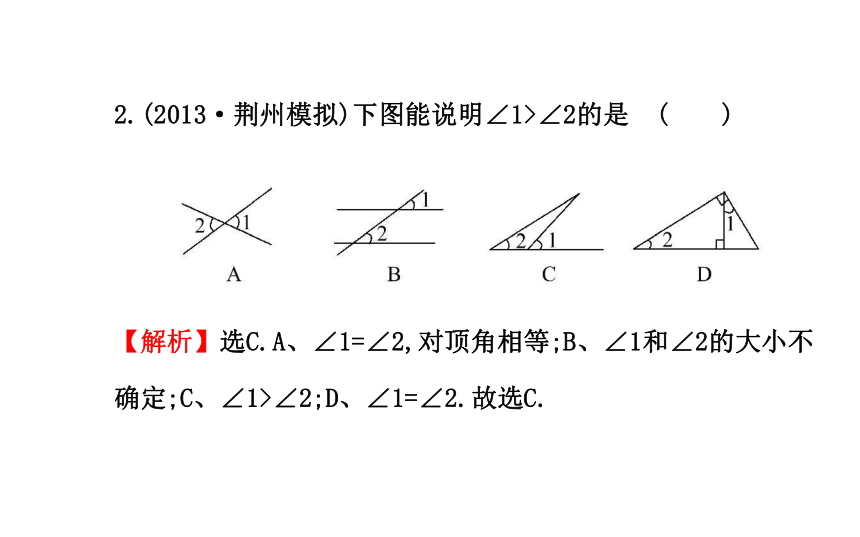
=180°-∠AOM=180°-38°=142°.2.(2013·荆州模拟)下图能说明∠1>∠2的是　(　　)
【解析】选C.A、∠1=∠2,对顶角相等;B、∠1和∠2的大小不确定;C、∠1>∠2;D、∠1=∠2.故选C.3.(2013·黄冈模拟)如图,直线AB,CD相交于点O,
OE⊥CD于O,OD平分∠BOF,∠BOE=50°,求∠AOC,
∠EOF和∠AOF的度数.
【解析】∵OE⊥CD,∴∠EOD=90°,又∠BOE=50°,
∴∠BOD=40°,又OD平分∠BOF,∴∠DOF=40°,
∴∠AOC=∠BOD=40°,∠EOF=∠EOD+∠DOF=90°+40°=130°,∠AOF=180°-∠FOB=180°-2∠DOF=180°-80°=100°.主题2 平行线的性质与判定
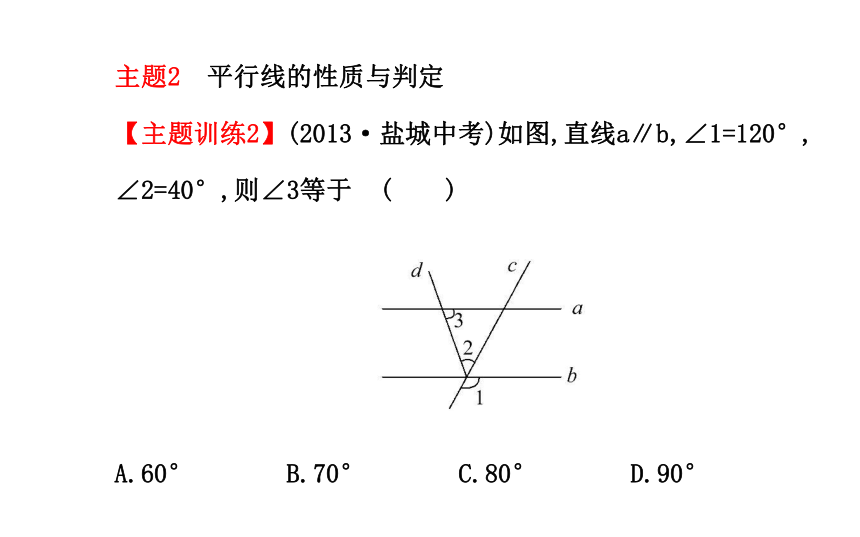
【主题训练2】(2013·盐城中考)如图,直线a∥b,∠1=120°,
∠2=40°,则∠3等于　(　　)
A.60°　 B.70°　 C.80°　 D.90°【自主解答】选C.如图所示,∵∠1与(∠2+∠4)是对顶角,
∴∠1=∠2+∠4.∴∠4=∠1-∠2=120°-40°=80°.
又∵a∥b,∴∠3=∠4.∴∠3=80°.【主题升华】
平行线的性质与判定
1.判定直线平行的五个途径
(1)同位角相等,两条直线平行.
(2)内错角相等,两条直线平行.
(3)同旁内角互补,两条直线平行.
(4)如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
(5)在同一平面内,垂直于同一条直线的两条直线平行.2.平行线的三条性质
(1)两条直线平行,同位角相等.
(2)两条直线平行,内错角相等.
(3)两条直线平行,同旁内角互补.
3.平行线的判定与性质的区别与联系
平行线的判定与性质之间正好是互为“因果”关系,即:平行线的判定是由角的相等或互补推出两直线平行,平行线的性质是由两直线平行推出角相等或互补,因此“欲证平行用判定,已知平行用性质”.1.(2013·宜昌中考)如图,已知AB∥CD,E是AB上一点,DE平分
∠BEC交CD于D,∠BEC=100°,则∠D的度数是　(　　)
A.100°　　　　B.80°　　　　C.60°　　　　D.50°
【解析】选D.∵DE平分∠BEC交CD于D,∠BEC=100°,∴∠BED=
∠BEC=50°,又∵AB∥CD,∴∠D =∠BED =50°.2.(2013·娄底中考)下列图形中,由AB∥CD,能使∠1=∠2成立的是　(　　)【解析】选B.A中,∠1,∠2是同旁内角,AB∥CD时不一定相等,A错误;B中,∠1,∠2的对顶角是同位角,AB∥CD时一定相等,B正确;C中,∠1,∠2是内错角,但是直线AC,BD被AD所截而成,AB∥CD时不一定相等,C错误;D中,∠1,∠2是同旁内角,且是直线AC,BD被AD所截而成,AB∥CD时不一定相等,D错误,故选B.3.(2013·白银中考)如图,把一块含有45°
的直角三角板的两个顶点放在直尺的对边
上,如果∠1=20°,那么∠2的度数是(　　)
A.15° B.20° C.25° D.30°
【解析】选C.因为直尺的两边互相平行,所以∠3=∠1=20°.所以∠2=45°-∠1=45°-20°=25°.4.(2013·仙桃中考)如图,已知直线AB∥CD,
∠GEB的平分线EF交CD于点F,∠1=40°,则
∠2等于　(　　)
A.130° B.140° C.150° D.160°
【解析】选D.∵AB∥CD,∠1=40°,∴∠GEB =∠1=40°,
∵EF平分∠GEB,∴∠FEB = ∠GEB =20°,∵AB∥CD,
∴∠FEB +∠2=180°,∴∠2=180°-∠FEB =160°.5.(2012·绵阳中考)如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=　　　　　　度.【解析】过点E作EM∥AB,
∵AB∥CD,∴EM∥AB∥CD.
∵∠1=30°,∠2=40°,
∴∠3=∠1=30°,∠4=∠2=40°,
∴∠BED=∠AEC=∠3+∠4=70°.
∵EF是∠BED的平分线,
∴∠BEF= ∠BED= ×70°=35°.
答案:35【知识拓展】相交线与平行线中的数学思想
1.转化思想:在几何推理中,已知条件和要求的结论之间常常需要转化.转化条件、转化问题是常用的推理形式,必要时还要添加辅助线进行转化.
2.分类讨论思想:在几何题中,有些题目未给出图形,这时我们就要结合题意画出图形,再解决问题.这一过程常具有多样性,我们需要分类讨论.3.方程思想:几何中常有一些求线段的长度或求角的大小的问题,对于这一类问题,我们可以借助题中的已知量与未知量之间的关系,想办法建立方程进行求解.