数学北师大版 九年级上册第四章 图形的相似:探索三角形相似的条件第4课时教学课件 17张PPT
文档属性
| 名称 | 数学北师大版 九年级上册第四章 图形的相似:探索三角形相似的条件第4课时教学课件 17张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 18:00:56 | ||
图片预览






文档简介
(共17张PPT)
第四章 图形的相似
4.4 探索三角形相似的条件
第 4 课时
学习目标
1.了解黄金分割.
2.能够运用黄金分割的知识解决简单的问题,发展应用意识.
复习引入
请同学们欣赏下面的图片.
为什么这些图片能使人感到和谐、平衡、舒适、美的感觉呢?你想知道其中的奥秘吗?那就让我们开始今天的学习吧!
想一想 一个五角星如图所示.
(1)从图中找出相等的角、相等的线段.
(2)在图中找出两对相似比不同的相似三角形.
L
K
H
G
F
E
D
C
B
A
探究新知
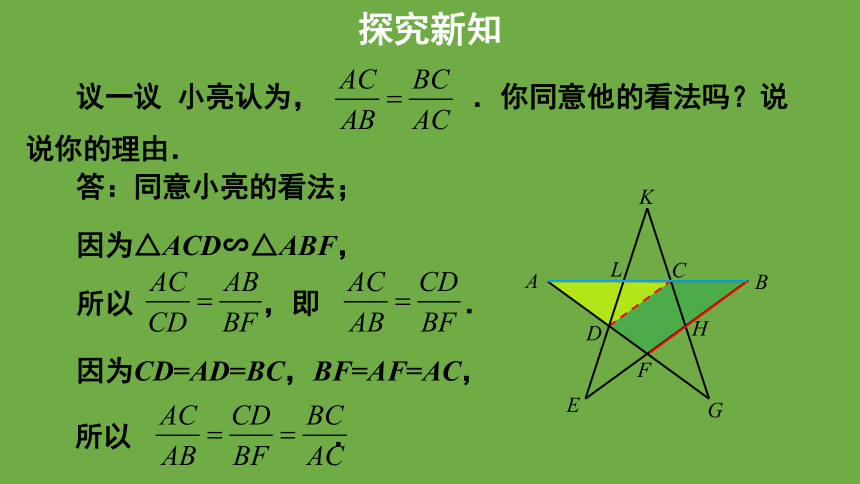
议一议 小亮认为, .你同意他的看法吗?说说你的理由.
答:同意小亮的看法;
因为△ACD∽△ABF,
所以 ,即 .
因为CD=AD=BC,BF=AF=AC,
所以 .
L
K
H
G
F
E
D
C
B
A
探究新知
一般地,点C把线段AB分成两条线段AC和BC(如图),如果 ,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.
A
C
B
探究新知
想一想 下图是古希腊时期的帕特农神庙,如果把图中表示的矩形画成下面右图中的ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD,那么我们可以惊奇地发现, .点E是AB的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?
探究新知
答:因为BC=EF=AE, ,
所以 ,即 .
所以点E是AB的黄金分割点.
(即 )是黄金比,也就是说,矩形ABCD的
宽与长的比是黄金比,这样的矩形称为黄金矩形.
探究新知
例 计算黄金比.
解:由 ,得AC2=AB·BC.
设AB=1,AC=x,则BC=1-x.
∴x2=1×(1-x),即x2+x-1=0.
解这个方程,得 ,
(不合题意,舍去)
所以,黄金比 .
典例精析
1.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165 cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( ).
A.4 cm B.6 cm
C.8 cm D.10 cm
C
课堂练习
课堂练习
2.如果点C为线段AB的黄金分割点,且AC>BC,则下列各式不正确的是( ).
A.AB∶AC=AC∶BC B.BC=
C.AC= D.AC≈0.618AB
3.已知点C为线段AB的黄金分割点,且AC>BC,则下列等式中正确的是( ).
A.AB2=AC·BC B.BC2=AC·AB
C.AC2=BC·AB D.AC2=2BC·AB
C
C
4.如果点C是线段AB的黄金分割点,且AC>BC,那么
的值是___________.
5.如图,电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20 m,则主持人应走到离点A至少_______ m处.如果她向点B再走_______ m,也处于比较得体的位置.(结果精确到0.1 m)
课堂练习
7.6
4.8
课堂练习
6.宽与长的比是 的矩形叫黄金矩形,心理学测试表明,黄金矩形令人赏心悦目,它给我们以协调、匀称的美感,现将同学们在教学活动中折叠黄金矩形的方法归纳出以下作图步骤(如图所示):
课堂练习
第一步:作一个任意正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD交AD的延长线于点F,
请你根据以上作法,说明矩形DCEF为黄金矩形(可取AB=2).
课堂练习
证明:在正方形ABCD中,取AB=2.
∵N为BC的中点,∴NC= BC=1.
在Rt△DNC中,
又∵NE=ND,
∴CE=NE-NC= -1.
∴ .
∴矩形DCEF为黄金矩形.
一般地,点C把线段AB分成两条线段AC和BC(如图),如果 ,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.
A
C
B
课堂小结
再见
第四章 图形的相似
4.4 探索三角形相似的条件
第 4 课时
学习目标
1.了解黄金分割.
2.能够运用黄金分割的知识解决简单的问题,发展应用意识.
复习引入
请同学们欣赏下面的图片.
为什么这些图片能使人感到和谐、平衡、舒适、美的感觉呢?你想知道其中的奥秘吗?那就让我们开始今天的学习吧!
想一想 一个五角星如图所示.
(1)从图中找出相等的角、相等的线段.
(2)在图中找出两对相似比不同的相似三角形.
L
K
H
G
F
E
D
C
B
A
探究新知
议一议 小亮认为, .你同意他的看法吗?说说你的理由.
答:同意小亮的看法;
因为△ACD∽△ABF,
所以 ,即 .
因为CD=AD=BC,BF=AF=AC,
所以 .
L
K
H
G
F
E
D
C
B
A
探究新知
一般地,点C把线段AB分成两条线段AC和BC(如图),如果 ,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.
A
C
B
探究新知
想一想 下图是古希腊时期的帕特农神庙,如果把图中表示的矩形画成下面右图中的ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD,那么我们可以惊奇地发现, .点E是AB的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗?
探究新知
答:因为BC=EF=AE, ,
所以 ,即 .
所以点E是AB的黄金分割点.
(即 )是黄金比,也就是说,矩形ABCD的
宽与长的比是黄金比,这样的矩形称为黄金矩形.
探究新知
例 计算黄金比.
解:由 ,得AC2=AB·BC.
设AB=1,AC=x,则BC=1-x.
∴x2=1×(1-x),即x2+x-1=0.
解这个方程,得 ,
(不合题意,舍去)
所以,黄金比 .
典例精析
1.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.如图,某女士身高165 cm,下半身长x与身高l的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( ).
A.4 cm B.6 cm
C.8 cm D.10 cm
C
课堂练习
课堂练习
2.如果点C为线段AB的黄金分割点,且AC>BC,则下列各式不正确的是( ).
A.AB∶AC=AC∶BC B.BC=
C.AC= D.AC≈0.618AB
3.已知点C为线段AB的黄金分割点,且AC>BC,则下列等式中正确的是( ).
A.AB2=AC·BC B.BC2=AC·AB
C.AC2=BC·AB D.AC2=2BC·AB
C
C
4.如果点C是线段AB的黄金分割点,且AC>BC,那么
的值是___________.
5.如图,电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20 m,则主持人应走到离点A至少_______ m处.如果她向点B再走_______ m,也处于比较得体的位置.(结果精确到0.1 m)
课堂练习
7.6
4.8
课堂练习
6.宽与长的比是 的矩形叫黄金矩形,心理学测试表明,黄金矩形令人赏心悦目,它给我们以协调、匀称的美感,现将同学们在教学活动中折叠黄金矩形的方法归纳出以下作图步骤(如图所示):
课堂练习
第一步:作一个任意正方形ABCD;
第二步:分别取AD,BC的中点M,N,连接MN;
第三步:以N为圆心,ND长为半径画弧,交BC的延长线于点E;
第四步:过点E作EF⊥AD交AD的延长线于点F,
请你根据以上作法,说明矩形DCEF为黄金矩形(可取AB=2).
课堂练习
证明:在正方形ABCD中,取AB=2.
∵N为BC的中点,∴NC= BC=1.
在Rt△DNC中,
又∵NE=ND,
∴CE=NE-NC= -1.
∴ .
∴矩形DCEF为黄金矩形.
一般地,点C把线段AB分成两条线段AC和BC(如图),如果 ,那么称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.
A
C
B
课堂小结
再见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
