3.2 用频率估计概率 课件(共18张PPT)2023--2024学年北师大版九年级数学上册
文档属性
| 名称 | 3.2 用频率估计概率 课件(共18张PPT)2023--2024学年北师大版九年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 117.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 18:12:17 | ||
图片预览





文档简介
(共18张PPT)
第三章 概率的进一步认识
3.2 用频率估计概率
1.经历试验、统计等活动,感受随机现象的特点,进一步发展交流合作的意识和能力.
2.能用试验频率估计一些随机事件发生的概率,进一步体会概率的意义.
一、学习目标
400个同学中,一定有2个同学的生日相同(可以不同年)吗?300个同学呢?
可有人说:“50个同学中,就很可能有2个同学的生日相同.”你同意这种说法吗?
二、情境引入
做一做:为了说明上述说法正确与否,我们可以通过大量重复试验,用“50个人中有2个人的生日相同”的频率来估计这一事件的概率.你能设计试验方案吗?
参考方案:
(1)每个同学课外调查10个人的生日.
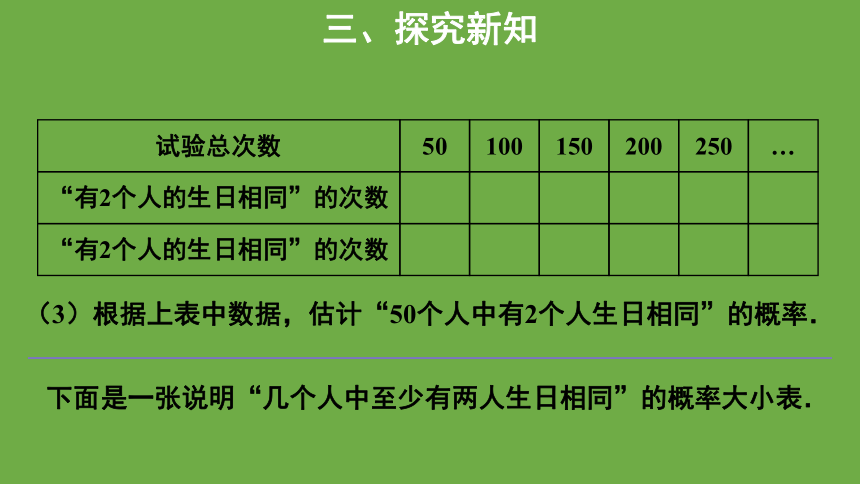
(2)从全班的调查结果中随机选取50个被调查人的生日,记录其中有无2个人的生日相同.每选取50个被调查人的生日为一次试验,重复尽可能多次试验,并将数据记录在下表中:
三、探究新知
试验总次数
50
100
150
200
250
…
“有2个人的生日相同”的次数
“有2个人的生日相同”的次数
(3)根据上表中数据,估计“50个人中有2个人生日相同”的概率.
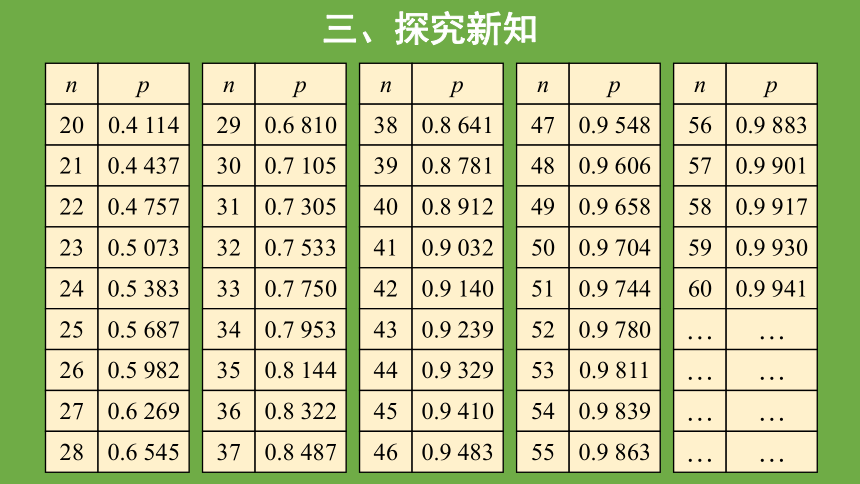
下面是一张说明“几个人中至少有两人生日相同”的概率大小表.
三、探究新知
n
p
20
0.4 114
21
0.4 437
22
0.4 757
23
0.5 073
24
0.5 383
25
0.5 687
26
0.5 982
27
0.6 269
28
0.6 545
n
p
38
0.8 641
39
0.8 781
40
0.8 912
41
0.9 032
42
0.9 140
43
0.9 239
44
0.9 329
45
0.9 410
46
0.9 483
n
p
29
0.6 810
30
0.7 105
31
0.7 305
32
0.7 533
33
0.7 750
34
0.7 953
35
0.8 144
36
0.8 322
37
0.8 487
n
p
47
0.9 548
48
0.9 606
49
0.9 658
50
0.9 704
51
0.9 744
52
0.9 780
53
0.9 811
54
0.9 839
55
0.9 863
n
p
56
0.9 883
57
0.9 901
58
0.9 917
59
0.9 930
60
0.9 941
…
…
…
…
…
…
…
…
三、探究新知
(1)一个口袋中有3个红球、7个白球,这些球除颜色外都相同.从口袋中随机摸出一个球,这个球是红球的概率是多少?
(2)一个口袋中有红球、白球共10个,这些球除颜色外都相同.如果不将球倒出来数,那么你能设计一个试验方案,估计其中红球和白球的比例吗?
四、典例精析
(2)从口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程,共摸100次,其中摸到红球n次,则其中红球和白球的比为n∶(100-n);
你还能提出并解决哪些与问题(2)类似的问题?
四、典例精析
解:(1)这个球是红球的概率是 ;
1.一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了100次,其中有10次摸到白球,因此小亮估计口袋中的红球大约有( )
A.45个 B.48个 C.50个 D.55个
A
五、课堂练习
2.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出1个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( )
A.6 B.10 C.18 D.20
D
五、课堂练习
3.在科学课外活动中,小明同学在相同的条件下做了某种作物种子发芽的试验,结果如下表所示.
由此估计这种作物种子发芽率约为____________
(结果保留小数点后两位).
0.94
五、课堂练习
种子数(个) 100 200 300 400
发芽种子数(个) 94 187 282 376
4.一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中.不断重复这一过程,共摸了100次球,发现有69次摸到红球.请你估计这个口袋中红球和白球的数量.
解:红球的数量为10×69%≈7(个),
白球的数量为10-7=3(个).
五、课堂练习
5.某篮球运动员在最近的几场大赛中罚球投篮的结果如下:
(1)计算表中各次比赛进球的频率;
(2)这位运动员投篮一次,进球的概率约为多少?
五、课堂练习
投篮次数n
8
10
12
9
16
10
进球次数m
6
8
9
7
12
7
进球频率
解:(1)填表如下:
(2)这位运动员投篮一次,进球的概率约为0.75.
五、课堂练习
投篮次数n
8
10
12
9
16
10
进球次数m
6
8
9
7
12
7
进球频率
0.75
0.8
0.75
0.78
0.75
0.7
1.一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.因此,我们可以通过大量重复试验,用一个随机事件发生的频率去估计它的概率.
六、课堂小结
2.频率与概率有什么区别与联系?
频率是随着试验次数的改变而变化的.而概率是一个常数,它是频率的科学抽象.当试验次数越来越多时,频率围绕概率摆动的平均幅度越来越小,即频率靠近概率.
六、课堂小结
六、课堂小结
3.当试验中各种结果发生的可能性相同时,用P(A)= (一次试验中,有n种等可能的结果,事件A包含其中的m种结果) 求概率;当试验的所有可能结果不是有限个或各种结果发生的可能性不相同时,可用频率来估计概率.
再 见
第三章 概率的进一步认识
3.2 用频率估计概率
1.经历试验、统计等活动,感受随机现象的特点,进一步发展交流合作的意识和能力.
2.能用试验频率估计一些随机事件发生的概率,进一步体会概率的意义.
一、学习目标
400个同学中,一定有2个同学的生日相同(可以不同年)吗?300个同学呢?
可有人说:“50个同学中,就很可能有2个同学的生日相同.”你同意这种说法吗?
二、情境引入
做一做:为了说明上述说法正确与否,我们可以通过大量重复试验,用“50个人中有2个人的生日相同”的频率来估计这一事件的概率.你能设计试验方案吗?
参考方案:
(1)每个同学课外调查10个人的生日.
(2)从全班的调查结果中随机选取50个被调查人的生日,记录其中有无2个人的生日相同.每选取50个被调查人的生日为一次试验,重复尽可能多次试验,并将数据记录在下表中:
三、探究新知
试验总次数
50
100
150
200
250
…
“有2个人的生日相同”的次数
“有2个人的生日相同”的次数
(3)根据上表中数据,估计“50个人中有2个人生日相同”的概率.
下面是一张说明“几个人中至少有两人生日相同”的概率大小表.
三、探究新知
n
p
20
0.4 114
21
0.4 437
22
0.4 757
23
0.5 073
24
0.5 383
25
0.5 687
26
0.5 982
27
0.6 269
28
0.6 545
n
p
38
0.8 641
39
0.8 781
40
0.8 912
41
0.9 032
42
0.9 140
43
0.9 239
44
0.9 329
45
0.9 410
46
0.9 483
n
p
29
0.6 810
30
0.7 105
31
0.7 305
32
0.7 533
33
0.7 750
34
0.7 953
35
0.8 144
36
0.8 322
37
0.8 487
n
p
47
0.9 548
48
0.9 606
49
0.9 658
50
0.9 704
51
0.9 744
52
0.9 780
53
0.9 811
54
0.9 839
55
0.9 863
n
p
56
0.9 883
57
0.9 901
58
0.9 917
59
0.9 930
60
0.9 941
…
…
…
…
…
…
…
…
三、探究新知
(1)一个口袋中有3个红球、7个白球,这些球除颜色外都相同.从口袋中随机摸出一个球,这个球是红球的概率是多少?
(2)一个口袋中有红球、白球共10个,这些球除颜色外都相同.如果不将球倒出来数,那么你能设计一个试验方案,估计其中红球和白球的比例吗?
四、典例精析
(2)从口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程,共摸100次,其中摸到红球n次,则其中红球和白球的比为n∶(100-n);
你还能提出并解决哪些与问题(2)类似的问题?
四、典例精析
解:(1)这个球是红球的概率是 ;
1.一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了100次,其中有10次摸到白球,因此小亮估计口袋中的红球大约有( )
A.45个 B.48个 C.50个 D.55个
A
五、课堂练习
2.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出1个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是( )
A.6 B.10 C.18 D.20
D
五、课堂练习
3.在科学课外活动中,小明同学在相同的条件下做了某种作物种子发芽的试验,结果如下表所示.
由此估计这种作物种子发芽率约为____________
(结果保留小数点后两位).
0.94
五、课堂练习
种子数(个) 100 200 300 400
发芽种子数(个) 94 187 282 376
4.一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中.不断重复这一过程,共摸了100次球,发现有69次摸到红球.请你估计这个口袋中红球和白球的数量.
解:红球的数量为10×69%≈7(个),
白球的数量为10-7=3(个).
五、课堂练习
5.某篮球运动员在最近的几场大赛中罚球投篮的结果如下:
(1)计算表中各次比赛进球的频率;
(2)这位运动员投篮一次,进球的概率约为多少?
五、课堂练习
投篮次数n
8
10
12
9
16
10
进球次数m
6
8
9
7
12
7
进球频率
解:(1)填表如下:
(2)这位运动员投篮一次,进球的概率约为0.75.
五、课堂练习
投篮次数n
8
10
12
9
16
10
进球次数m
6
8
9
7
12
7
进球频率
0.75
0.8
0.75
0.78
0.75
0.7
1.一般的随机事件,在做大量重复试验时,随着试验次数的增加,一个事件出现的频率,总在一个固定数的附近摆动,显示出一定的稳定性.因此,我们可以通过大量重复试验,用一个随机事件发生的频率去估计它的概率.
六、课堂小结
2.频率与概率有什么区别与联系?
频率是随着试验次数的改变而变化的.而概率是一个常数,它是频率的科学抽象.当试验次数越来越多时,频率围绕概率摆动的平均幅度越来越小,即频率靠近概率.
六、课堂小结
六、课堂小结
3.当试验中各种结果发生的可能性相同时,用P(A)= (一次试验中,有n种等可能的结果,事件A包含其中的m种结果) 求概率;当试验的所有可能结果不是有限个或各种结果发生的可能性不相同时,可用频率来估计概率.
再 见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
