4.4探索三角形相似的条件(一)同步练习 2022-2023学年北师大版九年级数学上册(含答案)
文档属性
| 名称 | 4.4探索三角形相似的条件(一)同步练习 2022-2023学年北师大版九年级数学上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 357.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 16:19:35 | ||
图片预览




文档简介
4.4探索三角形相似的条件 (一)同步练习
选择题(本大题共有10个小题,每小题3分,共30分)
1 .在△ABC与△A′B′C′中,∠B=∠B′=90°,∠A=30°,
则以下条件,不能说明△ABC与△A′B′C′相似的是( )
A.∠A′=30° B.∠C′=60° C.∠C=60° D.∠A′=2∠C′
2 . 如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E,
若线段DE=5,则线段BC的长为( )
A.7.5 B.10 C.15 D.20
3 . 如图,为估算学校的旗杆的高度,
身高米的小红同学沿着旗杆在地面的影子由向走去,
当她走到点处时,她的影子的顶端正好与旗杆的影子的顶端重合,
此时测得,,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
4 . 如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,
镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,
小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,
铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m B.15m C.20m D.16m
如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:
先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,
由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
A.AB=24m B.MN∥AB
C.△CMN∽△CAB D.CM:MA=1:2
6 ,如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,
设法使斜边DF保持水平,并且边DE与点B在同一直线上.
已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,
则树高AB为( )
A.12m B.13.5m C.15m D.16.5m
7 . 如图,在中,,于点D,,,
则AD的长是( )
A.1. B. C.2 D.4
如图,交于点D,,,,,
则的长等于( )
A. B. C. D.
9.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
10 . 如图,在等边中,点D,E分别是上的点,
,则( )
A.3 B. C. D.
填空题(本大题共有6个小题,每小题3分,共18分)
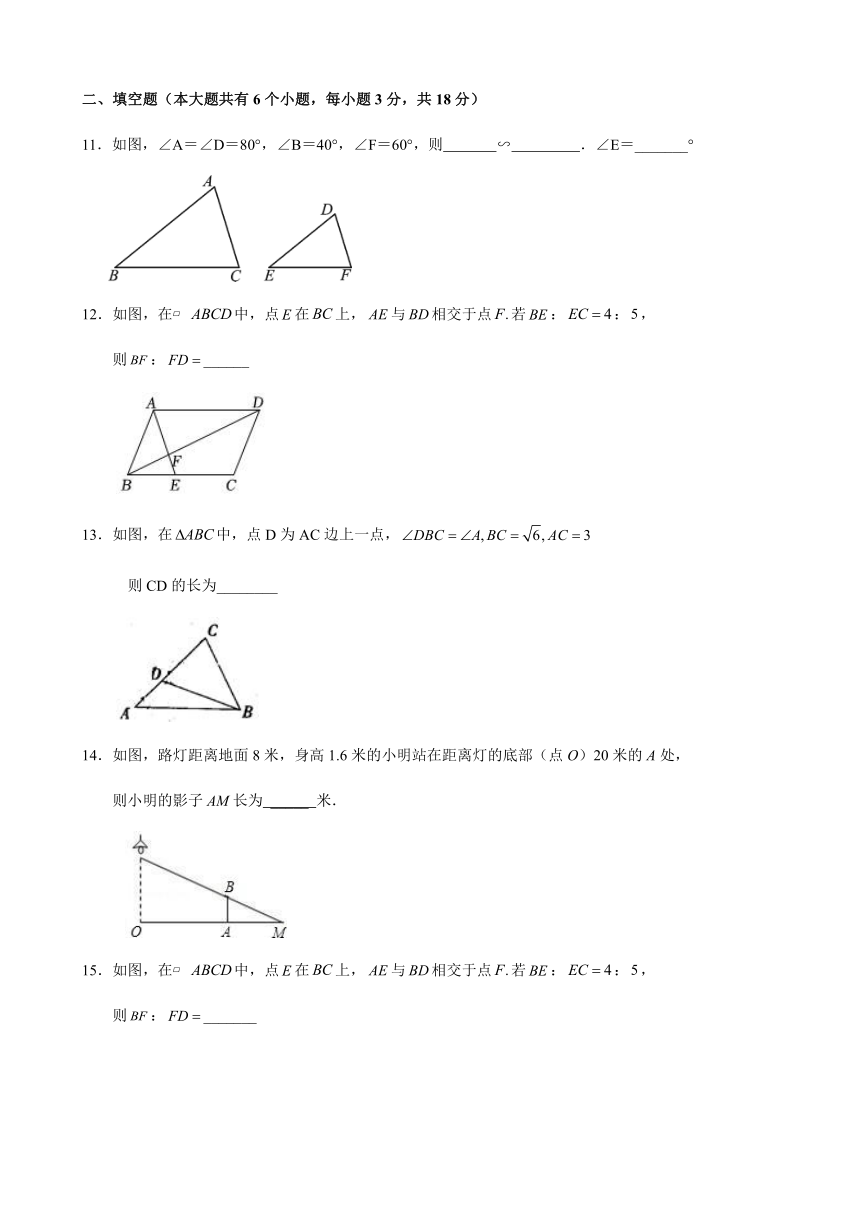
11.如图,∠A=∠D=80°,∠B=40°,∠F=60°,则 ∽ .∠E=_______°
如图,在 中,点在上,与相交于点若::,
则:______
如图,在中,点D为AC边上一点,
则CD的长为________
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,
则小明的影子AM长为 _____ 米.
如图,在 中,点在上,与相交于点若::,
则:_______
如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,
继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,
那么路灯A的高度AB等于( )
A.4.5米 B.6米 C.7.2米 D.8米
三、解答题(本大题共有7个小题,共52分)
17.如图,BE⊥AC于点E,AD⊥BC于点D,求证:.
18 . 如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,
试说明△ACE∽△BAD.
19 . 如图,已知D为内一点,E为外一点,且,.
求证:.
如图,操场上有一根旗杆AH,为测量它的高度,
在B和D处各立一根高米的标杆BC、DE,两杆相距30米,
测得视线AC与地面的交点为F,视线AE与地面的交点为G,
并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?
21.如图,在矩形ABCD中,E为BC上一点,DF⊥AE于点F.
(1)求证:△EAB∽△DFA;
(2)若AB=6,AD=12,BE=8,求DF的长.
22.如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.
(1)求证:△ACB∽△ADE;
(2)求AD的长度.
23.(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:AD·BC=AP·BP.
探究:如图2,在四边形ABCD中,点P为AB上一点,
当∠DPC=∠A=∠B=θ时,上述结论是否依然成立.说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,
由点A 出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),
当DC的长与△ABD底边上的高相等时,求t的值.
4.4探索三角形相似的条件 (一)同步练习(解答卷)
一、选择题(本大题共有10个小题,每小题3分,共30分)
1 .在△ABC与△A′B′C′中,∠B=∠B′=90°,∠A=30°,
则以下条件,不能说明△ABC与△A′B′C′相似的是( )
A.∠A′=30° B.∠C′=60° C.∠C=60° D.∠A′=2∠C′
【答案】C
2 . 如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E,
若线段DE=5,则线段BC的长为( )
A.7.5 B.10 C.15 D.20
【答案】C
3 . 如图,为估算学校的旗杆的高度,
身高米的小红同学沿着旗杆在地面的影子由向走去,
当她走到点处时,她的影子的顶端正好与旗杆的影子的顶端重合,
此时测得,,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
【答案】C
4 . 如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,
镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,
小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,
铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m B.15m C.20m D.16m
【答案】B
如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:
先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,
由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
A.AB=24m B.MN∥AB
C.△CMN∽△CAB D.CM:MA=1:2
【答案】D
6 ,如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,
设法使斜边DF保持水平,并且边DE与点B在同一直线上.
已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,
则树高AB为( )
A.12m B.13.5m C.15m D.16.5m
【答案】D
7 . 如图,在中,,于点D,,,
则AD的长是( )
A.1. B. C.2 D.4
【答案】D
如图,交于点D,,,,,
则的长等于( )
A. B. C. D.
【答案】A
9.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
10 . 如图,在等边中,点D,E分别是上的点,
,则( )
A.3 B. C. D.
【答案】D
二、填空题(本大题共有6个小题,每小题3分,共18分)
11.如图,∠A=∠D=80°,∠B=40°,∠F=60°,则 ∽ .∠E=_______°
【答案】40
如图,在 中,点在上,与相交于点若::,
则:______
【答案】:
如图,在中,点D为AC边上一点,
则CD的长为________
【答案】2
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,
则小明的影子AM长为 _____ 米.
【答案】5
如图,在 中,点在上,与相交于点若::,
则:______
【答案】:
如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,
继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,
那么路灯A的高度AB等于( )
A.4.5米 B.6米 C.7.2米 D.8米
【答案】B
三、解答题(本大题共有7个小题,共52分)
17.如图,BE⊥AC于点E,AD⊥BC于点D,求证:.
证明:在△ACD与△BCE中,
∵AD⊥BC于点D,BE⊥AC于点E,
∴∠D=∠E=90°,
又∵∠ACD=∠BCE,
∴△ACD∽△BCE,
∴.
18 . 如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,
试说明△ACE∽△BAD.
证明:∵CE=CD,
∴∠CED=∠CDE,
∴∠AEC=∠ADB,
∵∠DAC=∠B,
∴△ACE∽△BAD.
19 . 如图,已知D为内一点,E为外一点,且,.
求证:.
证明:,理由如下,
∵,,
∴,
∴,
变形得,
又∵,
∴,即,
∴.
如图,操场上有一根旗杆AH,为测量它的高度,
在B和D处各立一根高米的标杆BC、DE,两杆相距30米,
测得视线AC与地面的交点为F,视线AE与地面的交点为G,
并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?
解:由题意知,设AH=x,BH=y,
△AHF∽△CBF,△AHG∽△EDG,
∴,,
∴3x=1.5×(y+3),
5x=1.5×(y+30+5)
解得x=24m.
答:旗杆AH的高度为24m.
21.如图,在矩形ABCD中,E为BC上一点,DF⊥AE于点F.
(1)求证:△EAB∽△DFA;
(2)若AB=6,AD=12,BE=8,求DF的长.
(1)证明:∵DF⊥AE,
∴
∴
又∵AD∥BC,
∴∠DAE=∠AEB.
∴△ABE∽△DFA.
(2)根据题意可得:AE=10,
,
∴,
∴ ,
.
22.如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.
(1)求证:△ACB∽△ADE;
(2)求AD的长度.
证明:(1)证明:∵DE⊥AB,∠C=90°,
∴∠EDA=∠C=90°,
∵∠A=∠A,
∴△ACB∽△ADE;
(2)解:∵△ACB∽△ADE,
∴,
∴,
∴AD=4.
23.(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:AD·BC=AP·BP.
探究:如图2,在四边形ABCD中,点P为AB上一点,
当∠DPC=∠A=∠B=θ时,上述结论是否依然成立.说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,
由点A 出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),
当DC的长与△ABD底边上的高相等时,求t的值.
解:(1)如图1,
∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠APD=∠BPC,
∴△ADP∽△BPC,
∴,
∴ADBC=APBP;
(2)结论ADBC=APBP仍成立;
证明:如图2,∵∠BPD=∠DPC+∠BPC,
又∵∠BPD=∠A+∠APD,
∴∠DPC+∠BPC=∠A+∠APD,
∵∠DPC=∠A=θ,
∴∠BPC=∠APD,
又∵∠A=∠B=θ,
∴△ADP∽△BPC,
∴,
∴ADBC=APBP;
(3)如下图,过点D作DE⊥AB于点E,
∵AD=BD=5,AB=6,
∴AE=BE=3
∴DE==4,
∵以D为圆心,以DC为半径的圆与AB相切,
∴DC=DE=4,
∴BC=5-4=1,
∵AD=BD,
∴∠A=∠B,
又∵∠DPC=∠A,
∴∠DPC=∠A=∠B,
由(1)(2)的经验得AD BC=AP BP,
又∵AP=t,BP=6-t,
∴t(6-t)=5×1,
∴t=1或t=5,
∴t的值为1秒或5秒.
选择题(本大题共有10个小题,每小题3分,共30分)
1 .在△ABC与△A′B′C′中,∠B=∠B′=90°,∠A=30°,
则以下条件,不能说明△ABC与△A′B′C′相似的是( )
A.∠A′=30° B.∠C′=60° C.∠C=60° D.∠A′=2∠C′
2 . 如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E,
若线段DE=5,则线段BC的长为( )
A.7.5 B.10 C.15 D.20
3 . 如图,为估算学校的旗杆的高度,
身高米的小红同学沿着旗杆在地面的影子由向走去,
当她走到点处时,她的影子的顶端正好与旗杆的影子的顶端重合,
此时测得,,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
4 . 如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,
镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,
小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,
铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m B.15m C.20m D.16m
如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:
先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,
由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
A.AB=24m B.MN∥AB
C.△CMN∽△CAB D.CM:MA=1:2
6 ,如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,
设法使斜边DF保持水平,并且边DE与点B在同一直线上.
已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,
则树高AB为( )
A.12m B.13.5m C.15m D.16.5m
7 . 如图,在中,,于点D,,,
则AD的长是( )
A.1. B. C.2 D.4
如图,交于点D,,,,,
则的长等于( )
A. B. C. D.
9.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
10 . 如图,在等边中,点D,E分别是上的点,
,则( )
A.3 B. C. D.
填空题(本大题共有6个小题,每小题3分,共18分)
11.如图,∠A=∠D=80°,∠B=40°,∠F=60°,则 ∽ .∠E=_______°
如图,在 中,点在上,与相交于点若::,
则:______
如图,在中,点D为AC边上一点,
则CD的长为________
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,
则小明的影子AM长为 _____ 米.
如图,在 中,点在上,与相交于点若::,
则:_______
如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,
继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,
那么路灯A的高度AB等于( )
A.4.5米 B.6米 C.7.2米 D.8米
三、解答题(本大题共有7个小题,共52分)
17.如图,BE⊥AC于点E,AD⊥BC于点D,求证:.
18 . 如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,
试说明△ACE∽△BAD.
19 . 如图,已知D为内一点,E为外一点,且,.
求证:.
如图,操场上有一根旗杆AH,为测量它的高度,
在B和D处各立一根高米的标杆BC、DE,两杆相距30米,
测得视线AC与地面的交点为F,视线AE与地面的交点为G,
并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?
21.如图,在矩形ABCD中,E为BC上一点,DF⊥AE于点F.
(1)求证:△EAB∽△DFA;
(2)若AB=6,AD=12,BE=8,求DF的长.
22.如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.
(1)求证:△ACB∽△ADE;
(2)求AD的长度.
23.(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:AD·BC=AP·BP.
探究:如图2,在四边形ABCD中,点P为AB上一点,
当∠DPC=∠A=∠B=θ时,上述结论是否依然成立.说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,
由点A 出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),
当DC的长与△ABD底边上的高相等时,求t的值.
4.4探索三角形相似的条件 (一)同步练习(解答卷)
一、选择题(本大题共有10个小题,每小题3分,共30分)
1 .在△ABC与△A′B′C′中,∠B=∠B′=90°,∠A=30°,
则以下条件,不能说明△ABC与△A′B′C′相似的是( )
A.∠A′=30° B.∠C′=60° C.∠C=60° D.∠A′=2∠C′
【答案】C
2 . 如图,在△ABC中,点D在边AB上,BD=2AD,DE∥BC交AC于点E,
若线段DE=5,则线段BC的长为( )
A.7.5 B.10 C.15 D.20
【答案】C
3 . 如图,为估算学校的旗杆的高度,
身高米的小红同学沿着旗杆在地面的影子由向走去,
当她走到点处时,她的影子的顶端正好与旗杆的影子的顶端重合,
此时测得,,则旗杆的高度是( )
A.6.4m B.7m C.8m D.9m
【答案】C
4 . 如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,
镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,
小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,
铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m B.15m C.20m D.16m
【答案】B
如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:
先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,
由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
A.AB=24m B.MN∥AB
C.△CMN∽△CAB D.CM:MA=1:2
【答案】D
6 ,如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,
设法使斜边DF保持水平,并且边DE与点B在同一直线上.
已知纸板的两条边DF=50cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=20m,
则树高AB为( )
A.12m B.13.5m C.15m D.16.5m
【答案】D
7 . 如图,在中,,于点D,,,
则AD的长是( )
A.1. B. C.2 D.4
【答案】D
如图,交于点D,,,,,
则的长等于( )
A. B. C. D.
【答案】A
9.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
【答案】B
10 . 如图,在等边中,点D,E分别是上的点,
,则( )
A.3 B. C. D.
【答案】D
二、填空题(本大题共有6个小题,每小题3分,共18分)
11.如图,∠A=∠D=80°,∠B=40°,∠F=60°,则 ∽ .∠E=_______°
【答案】40
如图,在 中,点在上,与相交于点若::,
则:______
【答案】:
如图,在中,点D为AC边上一点,
则CD的长为________
【答案】2
如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,
则小明的影子AM长为 _____ 米.
【答案】5
如图,在 中,点在上,与相交于点若::,
则:______
【答案】:
如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,
继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,
那么路灯A的高度AB等于( )
A.4.5米 B.6米 C.7.2米 D.8米
【答案】B
三、解答题(本大题共有7个小题,共52分)
17.如图,BE⊥AC于点E,AD⊥BC于点D,求证:.
证明:在△ACD与△BCE中,
∵AD⊥BC于点D,BE⊥AC于点E,
∴∠D=∠E=90°,
又∵∠ACD=∠BCE,
∴△ACD∽△BCE,
∴.
18 . 如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,
试说明△ACE∽△BAD.
证明:∵CE=CD,
∴∠CED=∠CDE,
∴∠AEC=∠ADB,
∵∠DAC=∠B,
∴△ACE∽△BAD.
19 . 如图,已知D为内一点,E为外一点,且,.
求证:.
证明:,理由如下,
∵,,
∴,
∴,
变形得,
又∵,
∴,即,
∴.
如图,操场上有一根旗杆AH,为测量它的高度,
在B和D处各立一根高米的标杆BC、DE,两杆相距30米,
测得视线AC与地面的交点为F,视线AE与地面的交点为G,
并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?
解:由题意知,设AH=x,BH=y,
△AHF∽△CBF,△AHG∽△EDG,
∴,,
∴3x=1.5×(y+3),
5x=1.5×(y+30+5)
解得x=24m.
答:旗杆AH的高度为24m.
21.如图,在矩形ABCD中,E为BC上一点,DF⊥AE于点F.
(1)求证:△EAB∽△DFA;
(2)若AB=6,AD=12,BE=8,求DF的长.
(1)证明:∵DF⊥AE,
∴
∴
又∵AD∥BC,
∴∠DAE=∠AEB.
∴△ABE∽△DFA.
(2)根据题意可得:AE=10,
,
∴,
∴ ,
.
22.如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB于D.
(1)求证:△ACB∽△ADE;
(2)求AD的长度.
证明:(1)证明:∵DE⊥AB,∠C=90°,
∴∠EDA=∠C=90°,
∵∠A=∠A,
∴△ACB∽△ADE;
(2)解:∵△ACB∽△ADE,
∴,
∴,
∴AD=4.
23.(1)问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:AD·BC=AP·BP.
探究:如图2,在四边形ABCD中,点P为AB上一点,
当∠DPC=∠A=∠B=θ时,上述结论是否依然成立.说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,
由点A 出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),
当DC的长与△ABD底边上的高相等时,求t的值.
解:(1)如图1,
∵∠DPC=∠A=∠B=90°,
∴∠ADP+∠APD=90°,
∠BPC+∠APD=90°,
∴∠APD=∠BPC,
∴△ADP∽△BPC,
∴,
∴ADBC=APBP;
(2)结论ADBC=APBP仍成立;
证明:如图2,∵∠BPD=∠DPC+∠BPC,
又∵∠BPD=∠A+∠APD,
∴∠DPC+∠BPC=∠A+∠APD,
∵∠DPC=∠A=θ,
∴∠BPC=∠APD,
又∵∠A=∠B=θ,
∴△ADP∽△BPC,
∴,
∴ADBC=APBP;
(3)如下图,过点D作DE⊥AB于点E,
∵AD=BD=5,AB=6,
∴AE=BE=3
∴DE==4,
∵以D为圆心,以DC为半径的圆与AB相切,
∴DC=DE=4,
∴BC=5-4=1,
∵AD=BD,
∴∠A=∠B,
又∵∠DPC=∠A,
∴∠DPC=∠A=∠B,
由(1)(2)的经验得AD BC=AP BP,
又∵AP=t,BP=6-t,
∴t(6-t)=5×1,
∴t=1或t=5,
∴t的值为1秒或5秒.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
