不等式及其解法[上学期]
图片预览






文档简介
课件17张PPT。制作者:崧厦镇中学 高益兰
2005.10.18解一元一次不等式组 开始(§13.3 解一元一次不等式组)(§13.3 解一元一次不等式组)******引入新课讲授新课巩固练习提高练习复习小结退出问题:怎样求不等式 的解集?解:原不等式可化为两个不等式组:
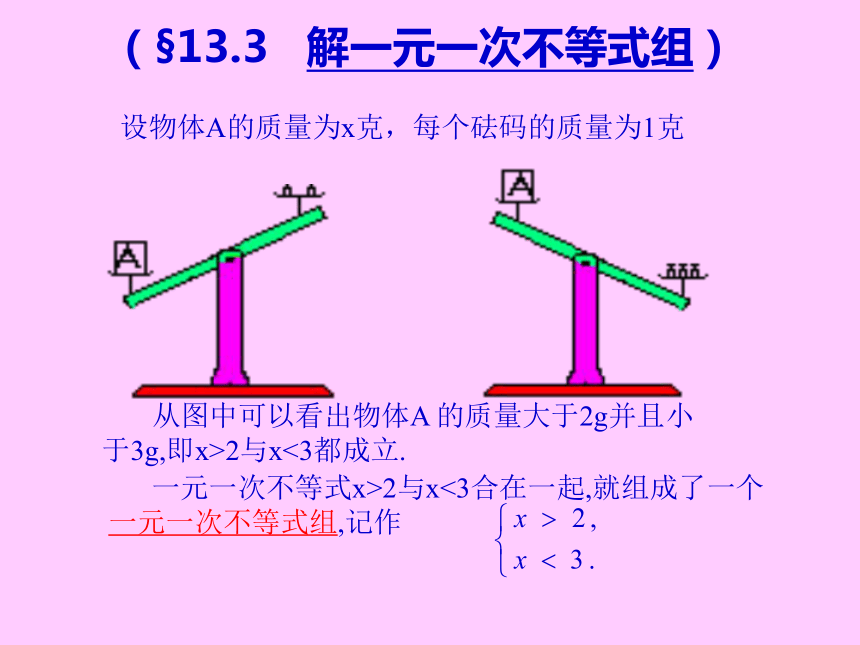
或 即 或解(1)得 , 解(2)得 .∴原不等式的解集是 或 .新课小结例2设物体A的质量为x克,每个砝码的质量为1克 从图中可以看出物体A 的质量大于2g并且小于3g,即x>2与x<3都成立. 一元一次不等式x>2与x<3合在一起,就组成了一个一元一次不等式组,记作(§13.3 解一元一次不等式组)叫做一元一次不等式组 的 ①②在同一数轴上表示不等式①,②的解集:在数轴上表示不等式的解集时应注意:
大于向右画,小于向左画;有等号的画实心圆点,无等号的画空心圆圈.①,②的解集的公共部分记作: 22.小小取小;
3.大小小大中间找,
4.大大小小找不到。选择题:(1)不等式组 的解集是( )(2)不等式组 的整数解是( )(3)不等式组 的负整数解是( ) ≤1D.不能确定. A. -2, 0, -1 , B. -2 , C. -2, -1, ≥-2,(4)不等式组 的解集在数轴上表示为( ) ≥-2,A.D.C.B.(5)如图, 则其解集是( )A.B.C.D.DCC-12.54BC≥2,≤2≤4≤4,§13.3 解一元一次不等式组小结: 1. 由几个一元一次不等式组所组成的不等式组叫做一 元一次不等式组 2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集. 3. 求不等式组的解集的过程,叫做解不等式组.4. 解简单一元一次不等式组的方法:(1)利用数轴找几个解集的公共部分:(2)利用规律: 大大取大,小小取小;大小小大中间找,大大小小找不到。作业例2. 求下列不等式组的解集:小结作业:
1. P87 Ex1, Ex2.
2. 《反馈》 §6.4 (1);
3. 补充题:完成下列表格 1.由几个一元一次不等式所组成的不等式组叫做一元一次不等式组. 2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集. 3.求不等式组的解集的过程,叫做解不等式组.概念:
2005.10.18解一元一次不等式组 开始(§13.3 解一元一次不等式组)(§13.3 解一元一次不等式组)******引入新课讲授新课巩固练习提高练习复习小结退出问题:怎样求不等式 的解集?解:原不等式可化为两个不等式组:
或 即 或解(1)得 , 解(2)得 .∴原不等式的解集是 或 .新课小结例2设物体A的质量为x克,每个砝码的质量为1克 从图中可以看出物体A 的质量大于2g并且小于3g,即x>2与x<3都成立. 一元一次不等式x>2与x<3合在一起,就组成了一个一元一次不等式组,记作(§13.3 解一元一次不等式组)叫做一元一次不等式组 的 ①②在同一数轴上表示不等式①,②的解集:在数轴上表示不等式的解集时应注意:
大于向右画,小于向左画;有等号的画实心圆点,无等号的画空心圆圈.①,②的解集的公共部分记作: 2
3.大小小大中间找,
4.大大小小找不到。选择题:(1)不等式组 的解集是( )(2)不等式组 的整数解是( )(3)不等式组 的负整数解是( ) ≤1D.不能确定. A. -2, 0, -1 , B. -2 , C. -2, -1, ≥-2,(4)不等式组 的解集在数轴上表示为( ) ≥-2,A.D.C.B.(5)如图, 则其解集是( )A.B.C.D.DCC-12.54BC≥2,≤2≤4≤4,§13.3 解一元一次不等式组小结: 1. 由几个一元一次不等式组所组成的不等式组叫做一 元一次不等式组 2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集. 3. 求不等式组的解集的过程,叫做解不等式组.4. 解简单一元一次不等式组的方法:(1)利用数轴找几个解集的公共部分:(2)利用规律: 大大取大,小小取小;大小小大中间找,大大小小找不到。作业例2. 求下列不等式组的解集:小结作业:
1. P87 Ex1, Ex2.
2. 《反馈》 §6.4 (1);
3. 补充题:完成下列表格 1.由几个一元一次不等式所组成的不等式组叫做一元一次不等式组. 2. 几个一元一次不等式的解集的公共部分,叫做由它们所组成的一元一次不等式组的解集. 3.求不等式组的解集的过程,叫做解不等式组.概念:
