1.1.3集合的基本运算课件-2023-2024学年高一上学期数学人教B版(2019)必修第一册(共20张PPT)
文档属性
| 名称 | 1.1.3集合的基本运算课件-2023-2024学年高一上学期数学人教B版(2019)必修第一册(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 771.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 23:33:17 | ||
图片预览







文档简介
(共20张PPT)
集合的基本运算
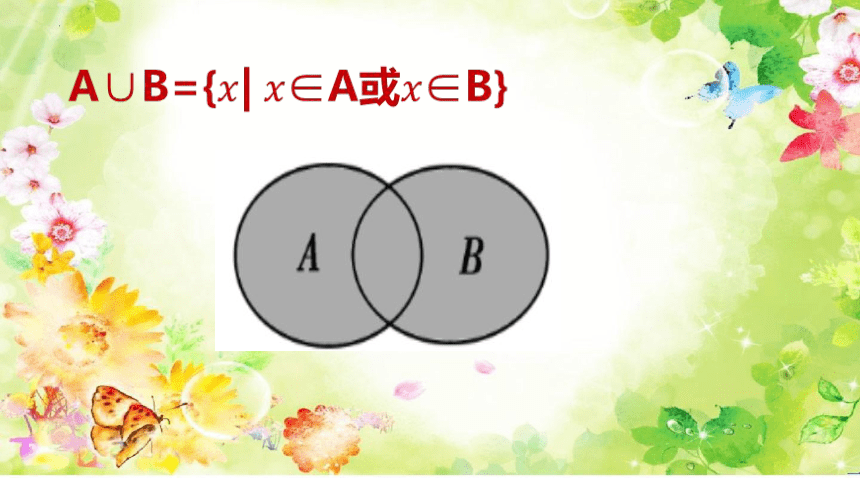
1、并集的概念
一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集,记作:
.
即v
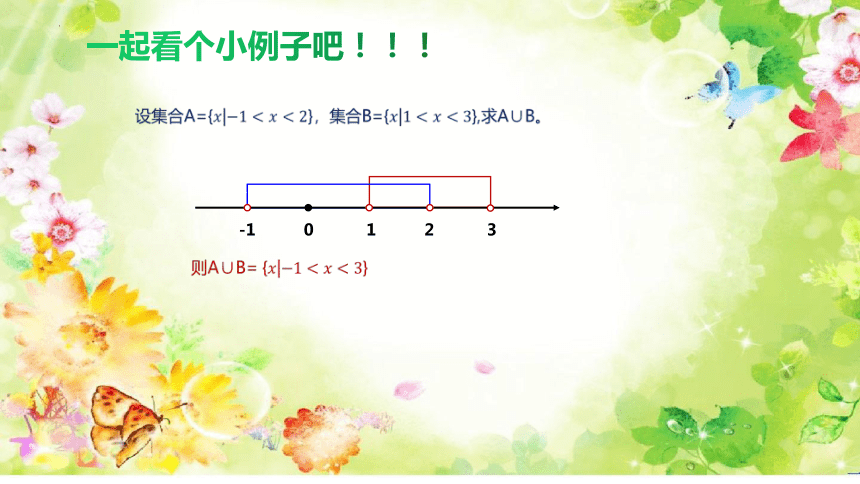
-1 0 1 2 3
一起看个小例子吧!!!
2、并集的性质
对于任意两个集合A,B,根据并集的概念可得:
①
;
一般地,由所有属于A集合且属于B集合的元素组成的集合,称为集合A与集合B的交集。记作:
A∩B,读作“A交B”
3、交集的概念
一起看个小题!!!!
已知集合
则
4、交集的性质
全集:一般地,如果一个集合中含有我们所研究的问题中涉及的所有元素,
那么就称这个集合为全集。也就是我们讨论的范围。一般记作“U”
5、补集的概念
设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},求 A, B.
解:根据题意可知:
U={1,2,3,4,5,6,7,8},
所以: A={4,5,6,7,8},
B= {1,2,7,8}.
6、补集的性质
随堂练习
4.设集合U={1,2,3,4,5,6},M={1,2,4},则 UM等于
A.U B.{1,3,5}
C.{3,5,6} D.{2,4,6}
√
5.设集合S={x|x>-2},T={x|-4≤x≤1},则( RS)∪T等于
A.{x|-2C.{x|x≤1} D.{x|x≥1}
√
6.设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则A∩( UB)=___.
{1}
解析 ∵ UB={1,5,6},
∴A∩( UB)={1}.
1.并集、交集概念
(1)对于并集,要注意其中“或”的意义,“或”与通常所说的“非此即彼”有原则性的区别,它们是“相容”的.“x∈A,或x∈B”这一条件,包括下列三种情况:x∈A但x B;x∈B但x A;x∈A且x∈B.因此,A∪B是由所有至少属于A、B两者之一的元素组成的集合.
(2)A∩B中的元素是“所有”属于集合A且属于集合B的元素,而不是部分,特别地,当集合A和集合B没有公共元素时,不能说A与B没有交集,而是A∩B= .
小结
2.全集与补集
(1)全集并非是包罗万象,含有任何元素的集合,它是对于研究问题而言的一个相对概念,它仅含有所研究问题中涉及的所有元素,如研究整数,Z就是全集,研究方程的实数解,R就是全集.因此,全集因研究问题而异.
(2)补集是集合之间的一种运算.求集合A的补集的前提是A是全集U的子集,随着所选全集的不同,得到的补集也是不同的,因此,它们是互相依存、不可分割的两个概念.
谢 谢!
集合的基本运算
1、并集的概念
一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集,记作:
.
即v
-1 0 1 2 3
一起看个小例子吧!!!
2、并集的性质
对于任意两个集合A,B,根据并集的概念可得:
①
;
一般地,由所有属于A集合且属于B集合的元素组成的集合,称为集合A与集合B的交集。记作:
A∩B,读作“A交B”
3、交集的概念
一起看个小题!!!!
已知集合
则
4、交集的性质
全集:一般地,如果一个集合中含有我们所研究的问题中涉及的所有元素,
那么就称这个集合为全集。也就是我们讨论的范围。一般记作“U”
5、补集的概念
设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},求 A, B.
解:根据题意可知:
U={1,2,3,4,5,6,7,8},
所以: A={4,5,6,7,8},
B= {1,2,7,8}.
6、补集的性质
随堂练习
4.设集合U={1,2,3,4,5,6},M={1,2,4},则 UM等于
A.U B.{1,3,5}
C.{3,5,6} D.{2,4,6}
√
5.设集合S={x|x>-2},T={x|-4≤x≤1},则( RS)∪T等于
A.{x|-2
√
6.设全集U={1,2,3,4,5,6},A={1,2},B={2,3,4},则A∩( UB)=___.
{1}
解析 ∵ UB={1,5,6},
∴A∩( UB)={1}.
1.并集、交集概念
(1)对于并集,要注意其中“或”的意义,“或”与通常所说的“非此即彼”有原则性的区别,它们是“相容”的.“x∈A,或x∈B”这一条件,包括下列三种情况:x∈A但x B;x∈B但x A;x∈A且x∈B.因此,A∪B是由所有至少属于A、B两者之一的元素组成的集合.
(2)A∩B中的元素是“所有”属于集合A且属于集合B的元素,而不是部分,特别地,当集合A和集合B没有公共元素时,不能说A与B没有交集,而是A∩B= .
小结
2.全集与补集
(1)全集并非是包罗万象,含有任何元素的集合,它是对于研究问题而言的一个相对概念,它仅含有所研究问题中涉及的所有元素,如研究整数,Z就是全集,研究方程的实数解,R就是全集.因此,全集因研究问题而异.
(2)补集是集合之间的一种运算.求集合A的补集的前提是A是全集U的子集,随着所选全集的不同,得到的补集也是不同的,因此,它们是互相依存、不可分割的两个概念.
谢 谢!
