7.4课题学习-镶嵌[下学期]
文档属性
| 名称 | 7.4课题学习-镶嵌[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-29 14:03:00 | ||
图片预览






文档简介
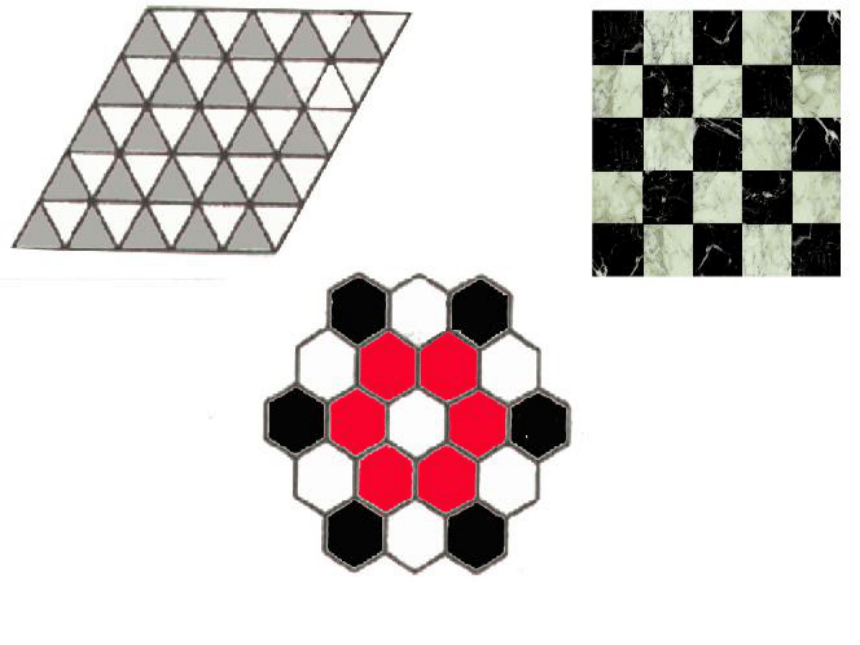
课件31张PPT。7.4 课题学习 镶嵌一、平面镶嵌
生活中,用地砖铺地、瓷砖贴墙,要求:
砖与砖严丝合缝,不留空隙,把地面全部覆
盖。
数学中:用一些不重叠摆放的多边形把平面
的一部分完全覆盖叫做多边形覆盖平面问题
(或平面镶嵌问题)
思考:
是否所有多边形都能镶嵌?满足的要求是
什么?
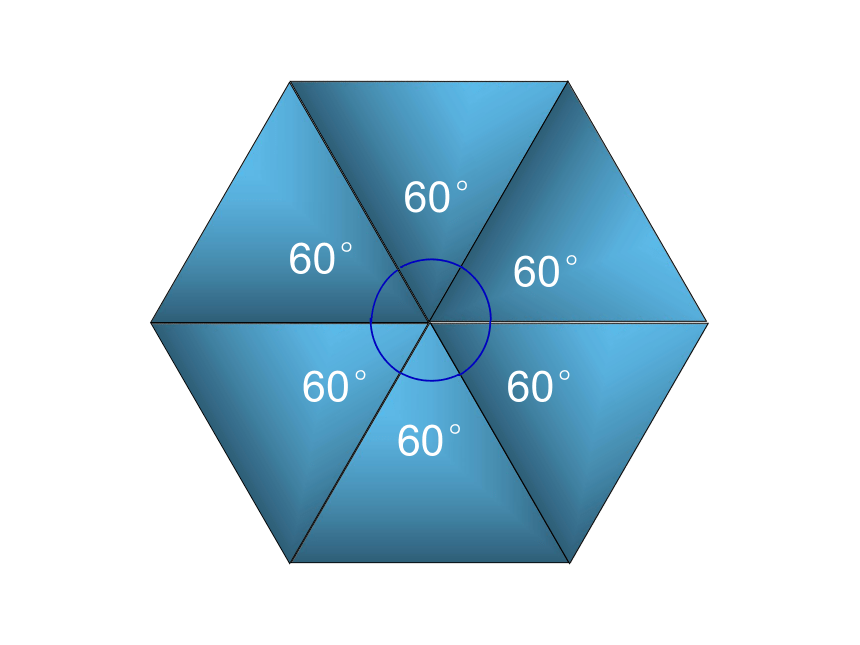
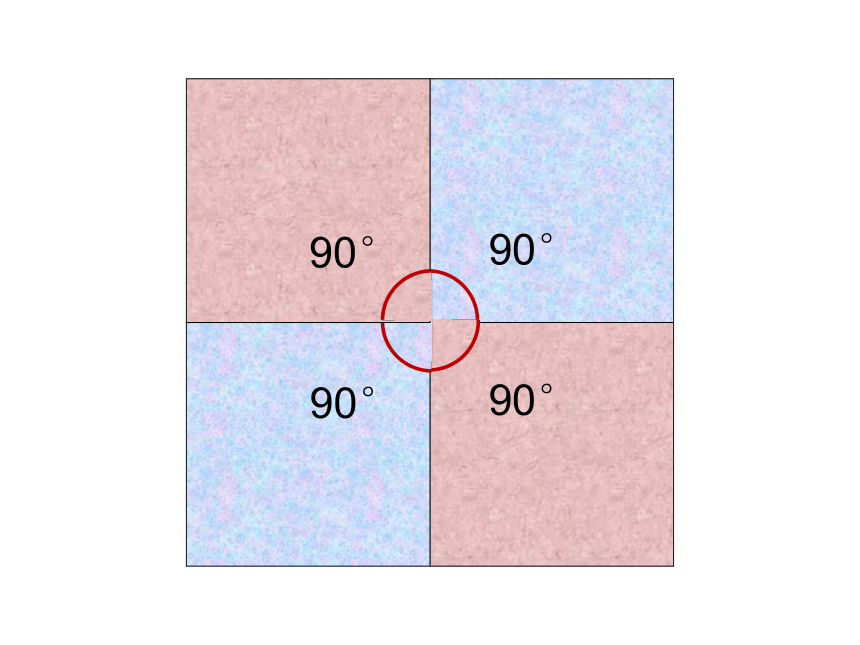
探索:1、哪一种正多边形能镶嵌?
同种正多边形个数×
正多边形内角度数=360o1。只用一种正多边形镶嵌的条件所需的个数:绕着一个顶点,能恰好围成一个周角
即:正多边形的一个内角的倍数是否是360°60°60°60°60°60°60°90°90°90°90°120°120°120°108°108°108°
(1)能用来拼地板的正多边形有:_________________________________
(2)不能能用来拼地板的正多边形有:_______________________________
(3)你的认识:
只用一种正多边形进行镶嵌 要用正多边形镶嵌成一个平面的关键是看:这种正多边形的一个内角的倍数是否是360°正三角形、正四边形、正六边形探索2、哪两种(几种)正多边形能镶嵌?镶嵌平面图案需要的什么条件?
拼接在同一个点的各个角的和恰好等于360度思考:当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个360°时,就拼成一个平面图形 2、哪两种多边形能镶嵌成一个平面图案?用其中两种正多变形镶嵌,哪两种正多变形能镶嵌?1、正三角形和正六边形两个多边形的个数关系?1。正六边形和正三角形的组合2、正方形和正八边形正八边形和正方形组合3、正十二边形和正三角形组合正十二边形和正三角形组合 二、两种用正多边形镶嵌的条件正多边形1个数×正多边形1内角度数+
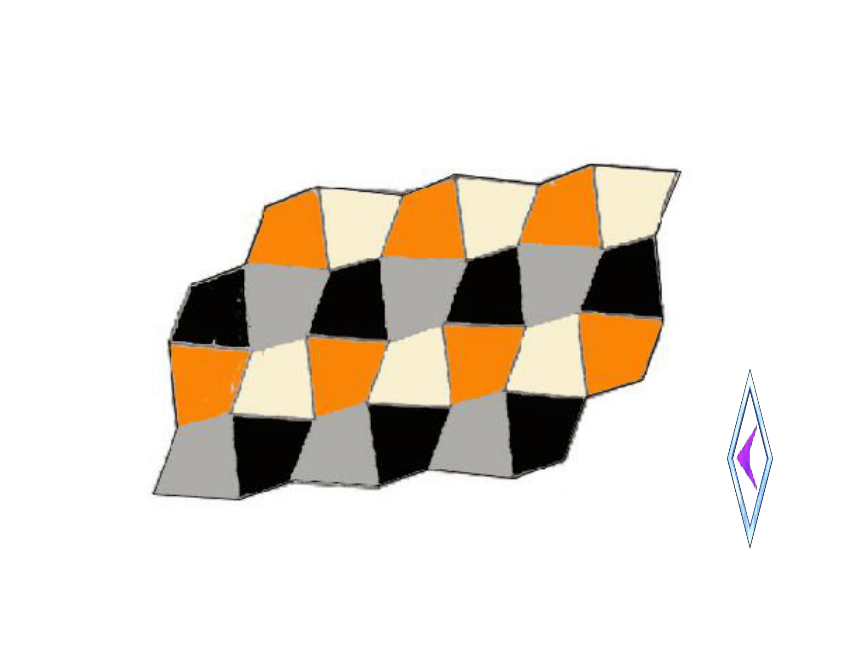
正多边形2个数×正多边形2内角度数=360o 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个360°时,就拼成一个平面图形 个数关系? 剪出一些形状、大小完全相同的任意三角形纸板,拼拼看,它们能否镶嵌成平面图案?1。只用一种正多边形镶嵌的条件 2、哪两种多边形能镶嵌 3.只用一种任意形状的多边形的镶嵌条件 剪出一些形状、大小完全相同的任意四边形纸板,拼拼看,它们能否镶嵌成平面图案?
问题只用一种任意形状的多边形的镶嵌条件回顾前面的镶嵌图案,你能说说它们是怎么镶嵌的?1. 能够铺满平面的正多边形组合是( )A. 正八边形和正方形B. 正五边形和正十边形C. 正六边形和正三角形课堂练习课堂小结周角360度是正多边形的一个内角度数的整
数倍时,用这样的正多边形能铺满平面!例如:用六个正三角形能铺满地面就是:6×60° =360°
用四个正方形能铺满地面就是: 4×90 °=360°课堂小结几种正多边形的组合,各取其中几个内角
相加恰为一个周角360度时,这样的正多
边形的组合能铺满平面。例如:正三角形和正方形。正三角形的内角为60度,正方形的
内角为90度,这样用3块正三角形和2块正方形,他们的内角和
为一个周角360度,所以能铺满地面。
生活中,用地砖铺地、瓷砖贴墙,要求:
砖与砖严丝合缝,不留空隙,把地面全部覆
盖。
数学中:用一些不重叠摆放的多边形把平面
的一部分完全覆盖叫做多边形覆盖平面问题
(或平面镶嵌问题)
思考:
是否所有多边形都能镶嵌?满足的要求是
什么?
探索:1、哪一种正多边形能镶嵌?
同种正多边形个数×
正多边形内角度数=360o1。只用一种正多边形镶嵌的条件所需的个数:绕着一个顶点,能恰好围成一个周角
即:正多边形的一个内角的倍数是否是360°60°60°60°60°60°60°90°90°90°90°120°120°120°108°108°108°
(1)能用来拼地板的正多边形有:_________________________________
(2)不能能用来拼地板的正多边形有:_______________________________
(3)你的认识:
只用一种正多边形进行镶嵌 要用正多边形镶嵌成一个平面的关键是看:这种正多边形的一个内角的倍数是否是360°正三角形、正四边形、正六边形探索2、哪两种(几种)正多边形能镶嵌?镶嵌平面图案需要的什么条件?
拼接在同一个点的各个角的和恰好等于360度思考:当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个360°时,就拼成一个平面图形 2、哪两种多边形能镶嵌成一个平面图案?用其中两种正多变形镶嵌,哪两种正多变形能镶嵌?1、正三角形和正六边形两个多边形的个数关系?1。正六边形和正三角形的组合2、正方形和正八边形正八边形和正方形组合3、正十二边形和正三角形组合正十二边形和正三角形组合 二、两种用正多边形镶嵌的条件正多边形1个数×正多边形1内角度数+
正多边形2个数×正多边形2内角度数=360o 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个360°时,就拼成一个平面图形 个数关系? 剪出一些形状、大小完全相同的任意三角形纸板,拼拼看,它们能否镶嵌成平面图案?1。只用一种正多边形镶嵌的条件 2、哪两种多边形能镶嵌 3.只用一种任意形状的多边形的镶嵌条件 剪出一些形状、大小完全相同的任意四边形纸板,拼拼看,它们能否镶嵌成平面图案?
问题只用一种任意形状的多边形的镶嵌条件回顾前面的镶嵌图案,你能说说它们是怎么镶嵌的?1. 能够铺满平面的正多边形组合是( )A. 正八边形和正方形B. 正五边形和正十边形C. 正六边形和正三角形课堂练习课堂小结周角360度是正多边形的一个内角度数的整
数倍时,用这样的正多边形能铺满平面!例如:用六个正三角形能铺满地面就是:6×60° =360°
用四个正方形能铺满地面就是: 4×90 °=360°课堂小结几种正多边形的组合,各取其中几个内角
相加恰为一个周角360度时,这样的正多
边形的组合能铺满平面。例如:正三角形和正方形。正三角形的内角为60度,正方形的
内角为90度,这样用3块正三角形和2块正方形,他们的内角和
为一个周角360度,所以能铺满地面。
