不等式的简单变形[下学期]

课件15张PPT。朋友们，欢迎你进入我们共同的课堂。执教者：傅方林回顾与探索解:3x-5x=-5+4……移项……合并同类项……将系数化为1等式的基本性质：-2x=-1X=等式的性质1 ：等式的两边都加上（或减去）同一个数或同一个整式，等式仍成立。(即如果a=b，那么a＋c=b＋c，a－c=b－c
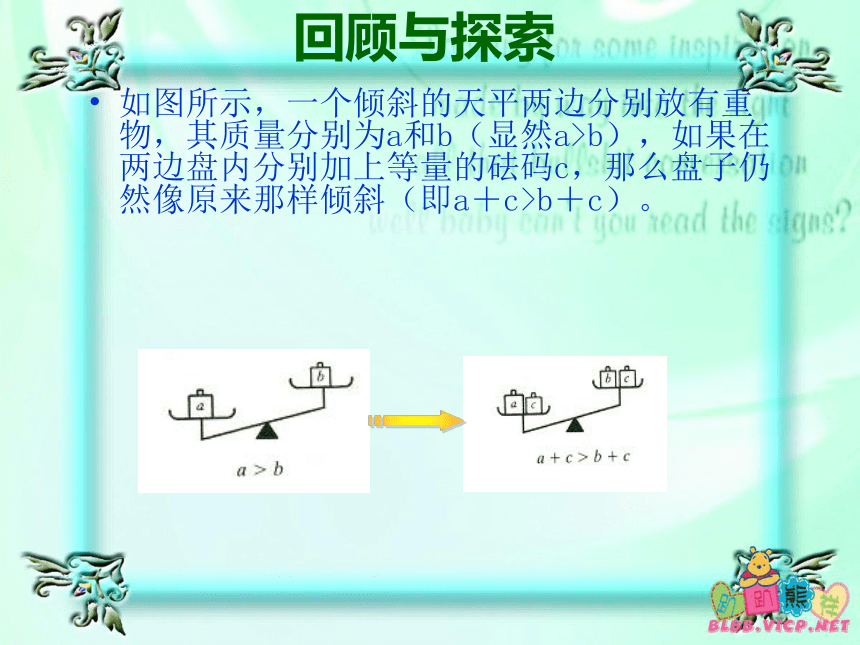
等式的性质2 ： 等式两边都乘以（或除以）一个不等于零的数，等式仍成立. (如果a=b，那么ac=bc c≠0) 第13章 一元一次不等式13.2不等式的简单变形如图所示，一个倾斜的天平两边分别放有重物，其质量分别为a和b（显然a>b），如果在两边盘内分别加上等量的砝码c，那么盘子仍然像原来那样倾斜（即a＋c>b＋c）。
回顾与探索不等式的性质1
如果a>b，那么a＋c>b＋c，a－c>b－c
这就是说，不等式的两边都加上（或减去）
同一个数或同一个整式，不等式的方向不变。
我发现了！　尝试探索例1：解不等式：
（1）x－7<8 （2）3x<2x-3这两小题中不等式的变形与方程的什么变形相类似？ 解： 两边都加上7得
解：两边都减去2x得 x-7+7 <8+7
3x-2x <2x-3-2x
移移x <8+7x <153x-2x <-3x <-3这里的变形与方程中的移项相类似：注意：移项要变号解下列不等式（1）x+2 >3 （2） 7x+7≤6x-2（3）-6（x-1）<-7（x+2）（4）6（x-1）>7（x+2） x > - 2 0不等式的两边都乘以（或除以）同一个不为零的数，不等号的方向是否也不变呢？将不等式7>4两边都乘以同一个数，比较所得的数的大小，用“<”或“>”填空：
7×3______4×3，
7×2_____4×2，
7×1_____4×1，
7×0_____4×0，
7×（－1）_____4×（－1），
7×（－2）_____4×（－2），
7×（－3）_____4×（－3），
……
从中你能发现什么？ 仔细想一想＞＞＞<<<=不等式的性质2
如果a>b，并且c>0，那么ac>bc。
不等式的性质3
如果a>b，并且c<0，那么ac这就是说，不等式两边都乘以（或除以）同一个正数，不等号的方向不变；不等式两边都乘以（或除以）同一个负数，不等号的方向改变。
这就是说，不等式两边都乘以（或除以）同一个正数，不等号的方向不变；不等式两边都乘以（或除以）同一个负数，不等号的方向改变。
我发现了！例题解析这两小题中不等式的变形与方程的什么变形相类似？有什么不同？解（1）不等式的两边都乘以2，不等号的方向不变，所以：
与解方程一样，解不等式的过程，就是要将不等式变形成x>a或x 的方向改变，所以
得 解下列不等式，并在数轴上表示出来：
1、X－2>0 2、X＋1>0
3、－2x<4 4、3x+3≤0
解：x >2。x >-1x >-2。x ≤-1.。 小游戏:你来出题我作答，看看到底谁最棒！发挥你的创意,每人出两题，由同桌解答，解好后再由出题人校对.x ≤ -28解：求不等式1-2x < 6的负整数解发挥集体的智慧,让我们共同努力思：要知道x的负整数解，首先应该求出一元一
次此不等式x的解集要使x的解是负整数，则x还必须小于0所以不等式的负整数解为 -2 、-1 1-2x < 6学习离不开总结！通过今天的探讨学习,你获得了哪些新知识?大胆说出来，和大家交流一下！1、解一元一次不等式的依据如果a>b，那么a＋c>b＋c，a－c>b－c如果a>b，并且c>0，那么ac>bc。如果a>b，并且c<0，那么ac