11.3.2三角形的内角和与外角和 课件(19张PPT)
文档属性
| 名称 | 11.3.2三角形的内角和与外角和 课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 15:31:20 | ||
图片预览



文档简介
(共19张PPT)
9.1.2 三角形的内角和与外角和
自主预习
知识回顾
认识知识
180
每两条边
另一边的反向延长线
1
2
互余
与它不相邻的两个内角
不相邻
分别取一个
360°
自主预习
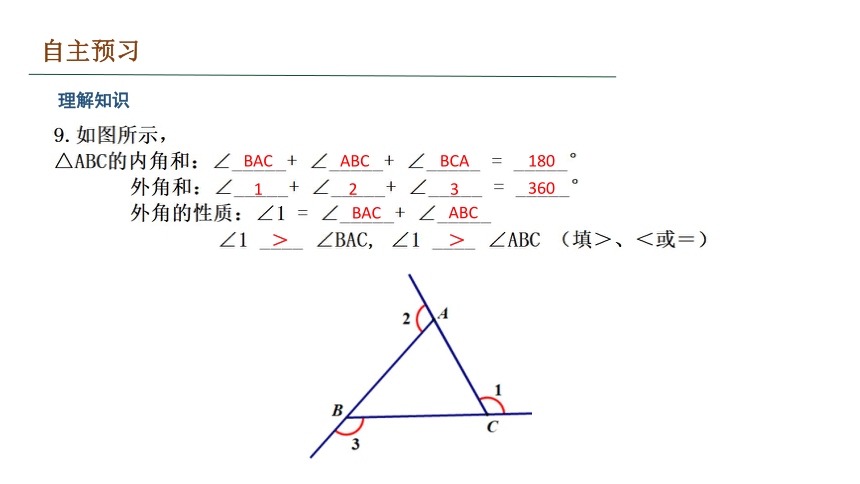
理解知识
BAC
ABC
BCA
180
360
1
2
3
BAC
ABC
>
>
问题一 探究三角形内角和
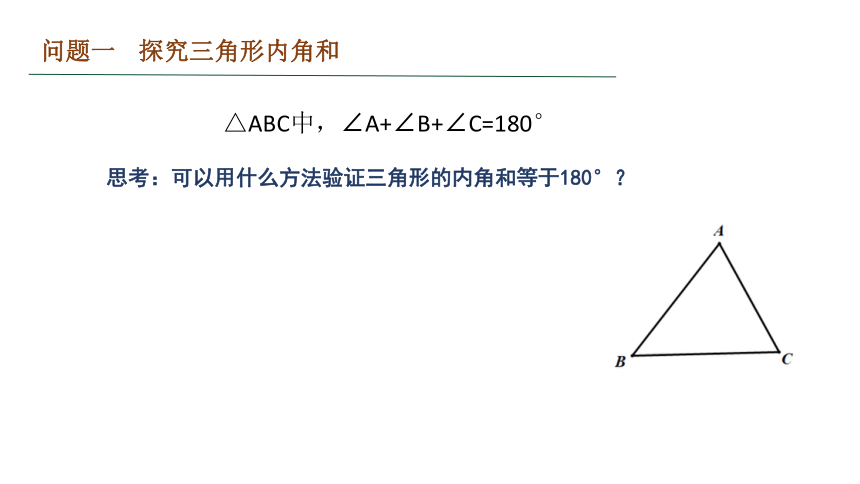
思考:可以用什么方法验证三角形的内角和等于180°?
△ABC中,∠A+∠B+∠C=180°
问题一 探究三角形内角和
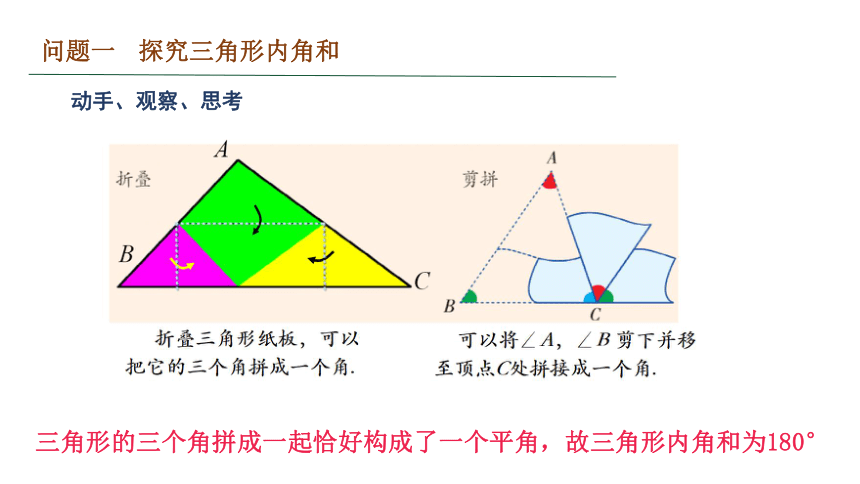
动手、观察、思考
三角形的三个角拼成一起恰好构成了一个平角,故三角形内角和为180°
证明:三角形的内角和为180°
E
D
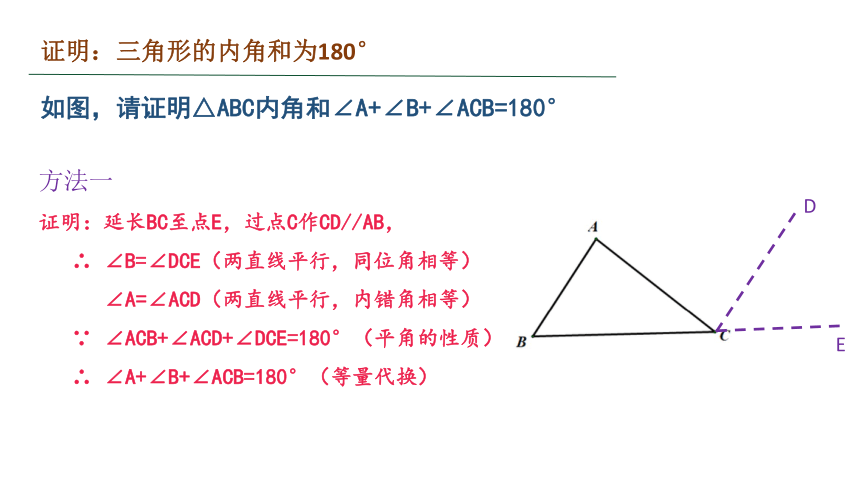
方法一
证明:延长BC至点E,过点C作CD//AB,
∴ ∠B=∠DCE(两直线平行,同位角相等)
∠A=∠ACD(两直线平行,内错角相等)
∵ ∠ACB+∠ACD+∠DCE=180°(平角的性质)
∴ ∠A+∠B+∠ACB=180°(等量代换)
如图,请证明△ABC内角和∠A+∠B+∠ACB=180°
证明:三角形的内角和为180°
E
D
方法二
证明:过点C作DE//AB,
∴ ∠A=∠ACD(两直线平行,内错角相等)
∠B=∠BCE(两直线平行,内错角相等)
∵ ∠ACB+∠ACD+∠BCE=180°(平角的性质)
∴ ∠A+∠B+∠ACB=180°(等量代换)
证明:三角形的内角和为180°
D
方法三
证明:过点C作CD//AB,
∴ ∠B+∠BCD=180°(两直线平行,同旁内角互补)
∠A=∠ACD(两直线平行,内错角相等)
∵ ∠BCD=∠ACB+∠ACD
∴ ∠A+∠B+∠ACB=180°(等量代换)
课后思考:证明三角形内角和的方法有很多,课后继续思考。
三角形内角和定理的推论
直角三角形中,两个锐角互余
如图,在△ABC中,∠B=90°,∠A和∠C有什么关系?
△ABC中,∠A+∠B+∠C=180°,
∠B=90°
∴ ∠A+∠C=90°
问题二:探究三角形的外角和
如图,△ABC,三个外角分别为∠1、∠2和∠3。
证明:∠1+∠2+∠3=360°
证明:∵ ∠1+∠ACB = 180°
∠2+∠BAC = 180°
∠3+∠ABC = 180°
∴ ∠1+∠2+∠3+∠ABC+∠BAC +∠ACB=540° (等式的性质)
又∵ ∠ABC+∠BAC +∠ACB=180°(三角形内角和等于180°)
∴ ∠1+∠2+∠3=360°
问题二:探究三角形的外角和
三角形的外角和:∠1+∠2+∠3=360°
什么是三角形的外角和?
从与每个内角相邻的两个外角中分别取一个相加得到的和称为三角形的外角和。
问题三:探究三角形外角的性质
如图,△ABC,其中一个外角∠ACD与它不相邻的内角∠A和∠B有什么关系?证明相关结论。
三角形的一个外角等于与它不相邻的两个内角的和
∵∠ACB +∠ACD=180°(平角的性质)
∠A+∠B+∠ACB=180°(三角形的内角和等于180°)
∴∠ACD=180°-∠ACB(等式的性质)
∠A+∠B =180°-∠ACB(等式的性质)
∴ ∠ACD =∠A+∠B(等量代换)
∠ACD>∠A,∠ACD>∠B
三角形的一个外角大于任何一个与它不相邻的内角
问题三:知识综合应用
如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°,求:
(1)∠B的度数;
(2)∠C的度数。
解:(1)∵ ∠ADC是△ABD的外角(已知)
∴∠B+∠BAD =∠ADC = 80°(三角形的一个外角
等于与它不相邻的两个内角和)
又∵ ∠B=∠BAD(已知)
∴∠B=80°× =40°(等量代换)
(2)∵∠B+∠BAC+∠C=180°(三角形内角和等于180°)
∴∠C=180°-∠B-∠BAC=180°-40°-70°
=70°
总结归纳
三角形的内角和
内容:三角形的内角和等于180°
推论:直角三角形的两个锐角互余
三角形的外角
性质:1.三角形的一个外角等于与它不相邻的两个内角的和;
2.三角形的一个外角大于任何一个与它不相邻的内角。
外角和:三角形的外角和等于360°
三角形的内角和与外角和
训练检测
A
B
知识点:三角形内角和180°
知识点:三角形的一个外角大于任何一个与它不相邻的内角。
训练检测
D
B
知识点:三角形外角和360°
三角形内角、外角及平行线性质的综合应用。
训练检测
C
三角形知识的综合应用。
课后作业
完成 同步练习册P52 9.1 三角形(三)
谢 谢!
9.1.2 三角形的内角和与外角和
自主预习
知识回顾
认识知识
180
每两条边
另一边的反向延长线
1
2
互余
与它不相邻的两个内角
不相邻
分别取一个
360°
自主预习
理解知识
BAC
ABC
BCA
180
360
1
2
3
BAC
ABC
>
>
问题一 探究三角形内角和
思考:可以用什么方法验证三角形的内角和等于180°?
△ABC中,∠A+∠B+∠C=180°
问题一 探究三角形内角和
动手、观察、思考
三角形的三个角拼成一起恰好构成了一个平角,故三角形内角和为180°
证明:三角形的内角和为180°
E
D
方法一
证明:延长BC至点E,过点C作CD//AB,
∴ ∠B=∠DCE(两直线平行,同位角相等)
∠A=∠ACD(两直线平行,内错角相等)
∵ ∠ACB+∠ACD+∠DCE=180°(平角的性质)
∴ ∠A+∠B+∠ACB=180°(等量代换)
如图,请证明△ABC内角和∠A+∠B+∠ACB=180°
证明:三角形的内角和为180°
E
D
方法二
证明:过点C作DE//AB,
∴ ∠A=∠ACD(两直线平行,内错角相等)
∠B=∠BCE(两直线平行,内错角相等)
∵ ∠ACB+∠ACD+∠BCE=180°(平角的性质)
∴ ∠A+∠B+∠ACB=180°(等量代换)
证明:三角形的内角和为180°
D
方法三
证明:过点C作CD//AB,
∴ ∠B+∠BCD=180°(两直线平行,同旁内角互补)
∠A=∠ACD(两直线平行,内错角相等)
∵ ∠BCD=∠ACB+∠ACD
∴ ∠A+∠B+∠ACB=180°(等量代换)
课后思考:证明三角形内角和的方法有很多,课后继续思考。
三角形内角和定理的推论
直角三角形中,两个锐角互余
如图,在△ABC中,∠B=90°,∠A和∠C有什么关系?
△ABC中,∠A+∠B+∠C=180°,
∠B=90°
∴ ∠A+∠C=90°
问题二:探究三角形的外角和
如图,△ABC,三个外角分别为∠1、∠2和∠3。
证明:∠1+∠2+∠3=360°
证明:∵ ∠1+∠ACB = 180°
∠2+∠BAC = 180°
∠3+∠ABC = 180°
∴ ∠1+∠2+∠3+∠ABC+∠BAC +∠ACB=540° (等式的性质)
又∵ ∠ABC+∠BAC +∠ACB=180°(三角形内角和等于180°)
∴ ∠1+∠2+∠3=360°
问题二:探究三角形的外角和
三角形的外角和:∠1+∠2+∠3=360°
什么是三角形的外角和?
从与每个内角相邻的两个外角中分别取一个相加得到的和称为三角形的外角和。
问题三:探究三角形外角的性质
如图,△ABC,其中一个外角∠ACD与它不相邻的内角∠A和∠B有什么关系?证明相关结论。
三角形的一个外角等于与它不相邻的两个内角的和
∵∠ACB +∠ACD=180°(平角的性质)
∠A+∠B+∠ACB=180°(三角形的内角和等于180°)
∴∠ACD=180°-∠ACB(等式的性质)
∠A+∠B =180°-∠ACB(等式的性质)
∴ ∠ACD =∠A+∠B(等量代换)
∠ACD>∠A,∠ACD>∠B
三角形的一个外角大于任何一个与它不相邻的内角
问题三:知识综合应用
如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°,求:
(1)∠B的度数;
(2)∠C的度数。
解:(1)∵ ∠ADC是△ABD的外角(已知)
∴∠B+∠BAD =∠ADC = 80°(三角形的一个外角
等于与它不相邻的两个内角和)
又∵ ∠B=∠BAD(已知)
∴∠B=80°× =40°(等量代换)
(2)∵∠B+∠BAC+∠C=180°(三角形内角和等于180°)
∴∠C=180°-∠B-∠BAC=180°-40°-70°
=70°
总结归纳
三角形的内角和
内容:三角形的内角和等于180°
推论:直角三角形的两个锐角互余
三角形的外角
性质:1.三角形的一个外角等于与它不相邻的两个内角的和;
2.三角形的一个外角大于任何一个与它不相邻的内角。
外角和:三角形的外角和等于360°
三角形的内角和与外角和
训练检测
A
B
知识点:三角形内角和180°
知识点:三角形的一个外角大于任何一个与它不相邻的内角。
训练检测
D
B
知识点:三角形外角和360°
三角形内角、外角及平行线性质的综合应用。
训练检测
C
三角形知识的综合应用。
课后作业
完成 同步练习册P52 9.1 三角形(三)
谢 谢!
