1.3 探索三角形全等的条件培优专题三 全等三角形的几种常见模型应用同步训练(含答案)
文档属性
| 名称 | 1.3 探索三角形全等的条件培优专题三 全等三角形的几种常见模型应用同步训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-18 22:11:22 | ||
图片预览


文档简介
第一章 三角形
3 探索三角形全等的条件
培优专题三 全等三角形的几种常见模型应用
类型 1 平移模型
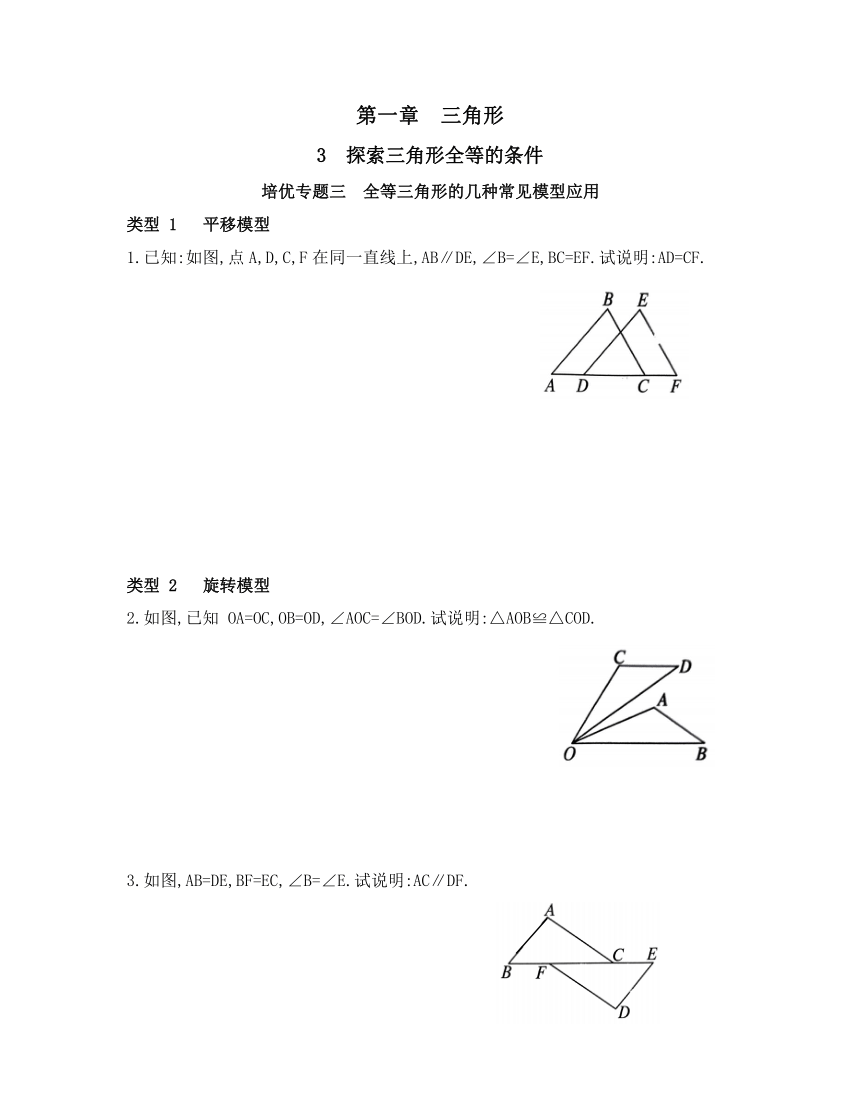
1.已知:如图,点A,D,C,F在同一直线上,AB∥DE,∠B=∠E,BC=EF.试说明:AD=CF.
类型 2 旋转模型
2.如图,已知 OA=OC,OB=OD,∠AOC=∠BOD.试说明:△AOB≌△COD.
3.如图,AB=DE,BF=EC,∠B=∠E.试说明:AC∥DF.
4.如图,D是△ABC 的边 AB上一点,CF∥AB,DF交AC 于E点,DE=EF.
(1)试说明:△ADE≌△CFE;
(2)若AB=5,CF=4,求BD的长.
5.如图,点B为 AC上一点,AD∥CE,∠DBC+∠BEC=180°,BD=EB.试说明:AD=BC.
类型3 对称模型
6.如图,AC平分∠BAD,CB⊥AB,CD⊥AD,垂足分别为 B,D.
(1)试说明:△ABC≌△ADC;
(2)若AB=4,CD=3,求四边形 ABCD的面积.
7.如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点 E,连接DE.
(1)试说明:△ABE≌△DBE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
类型 4 一线三等角模型
8.如图,在△ABC中,AB=AC,点 D,A,E都在直线上,并且∠BDA=∠AEC=∠BAC=α.
若CE=a,BD=b,求 DE 的长度(用含 a,b的代数式表示).
参考答案
1.解:因为 AB∥DE,所以∠A=∠EDF.
在△ABC和△DEF中, 所以△ABC≌△DEF(AAS).
所以AC=DF,所以AC-DC=DF-DC,即 AD=CF.
2.解:因为∠AOC=∠BOD,所以∠AOC-∠AOD=∠BOD-∠AOD,即∠COD=∠AOB.
在△AOB 和△COD中, 所以△AOB≌△COD(SAS).
3.解:因为 BF=EC,所以BF+FC=EC+FC,即 BC=EF.
在△ABC 和△DEF中, 所以△ABC≌△DEF(SAS).
所以∠ACB=∠DFE,所以AC∥DF.
4.解:(1)因为 CF∥AB,所以∠ADF=∠F,∠A=∠ECF.
在△ADE和△CFE中, 所以△ADE≌△CFE(AAS).
(2)因为△ADE≌△CFE,所以AD=CF=4.
所以BD=AB-AD=5-4=1.
5.解:因为 AD∥EC,所以∠A=∠C.
因为∠DBC+∠ABD=180°,∠DBC+∠BEC=180°,所以∠ABD=∠CEB.
又BD=EB,所以△ADB≌△CBE(AAS).所以AD=BC.
6.解:(1)因为AC平分∠BAD,所以∠BAC=∠DAC.
因为CB⊥AB,CD⊥AD,所以∠B=∠D=90°.
在△ABC和△ADC中, 所以△ABC≌△ADC(AAS).
(2)由(1)知:△ABC≌△ADC,所以
所以 所以
所以
故四边形 ABCD的面积是 12.
7.解:(1)因为 BE平分∠ABC,所以∠ABE=∠DBE.
在△ABE和△DBE中, 所以△ABE≌△DBE(SAS).
(2)因为∠A=100°,∠C=50°,所以∠ABC=30°.
因为BE平分∠ABC,所以
在△ABE中,∠AEB=180°—∠A—∠ABE=180°—100°—15°=65°.
8.解:因为∠BDA=∠BAC=α,所以∠ABD+∠BAD=180°-α=∠BAD+∠CAE.
所以∠ABD=∠CAE.
在△ABD和△CAE中, 所以△ABD≌△CAE(AAS).
所以AD=CE,BD=AE.
因为 CE=a,BD=b,所以DE=AD+AE=CE+BD=a+b.
3 探索三角形全等的条件
培优专题三 全等三角形的几种常见模型应用
类型 1 平移模型
1.已知:如图,点A,D,C,F在同一直线上,AB∥DE,∠B=∠E,BC=EF.试说明:AD=CF.
类型 2 旋转模型
2.如图,已知 OA=OC,OB=OD,∠AOC=∠BOD.试说明:△AOB≌△COD.
3.如图,AB=DE,BF=EC,∠B=∠E.试说明:AC∥DF.
4.如图,D是△ABC 的边 AB上一点,CF∥AB,DF交AC 于E点,DE=EF.
(1)试说明:△ADE≌△CFE;
(2)若AB=5,CF=4,求BD的长.
5.如图,点B为 AC上一点,AD∥CE,∠DBC+∠BEC=180°,BD=EB.试说明:AD=BC.
类型3 对称模型
6.如图,AC平分∠BAD,CB⊥AB,CD⊥AD,垂足分别为 B,D.
(1)试说明:△ABC≌△ADC;
(2)若AB=4,CD=3,求四边形 ABCD的面积.
7.如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点 E,连接DE.
(1)试说明:△ABE≌△DBE;
(2)若∠A=100°,∠C=50°,求∠AEB的度数.
类型 4 一线三等角模型
8.如图,在△ABC中,AB=AC,点 D,A,E都在直线上,并且∠BDA=∠AEC=∠BAC=α.
若CE=a,BD=b,求 DE 的长度(用含 a,b的代数式表示).
参考答案
1.解:因为 AB∥DE,所以∠A=∠EDF.
在△ABC和△DEF中, 所以△ABC≌△DEF(AAS).
所以AC=DF,所以AC-DC=DF-DC,即 AD=CF.
2.解:因为∠AOC=∠BOD,所以∠AOC-∠AOD=∠BOD-∠AOD,即∠COD=∠AOB.
在△AOB 和△COD中, 所以△AOB≌△COD(SAS).
3.解:因为 BF=EC,所以BF+FC=EC+FC,即 BC=EF.
在△ABC 和△DEF中, 所以△ABC≌△DEF(SAS).
所以∠ACB=∠DFE,所以AC∥DF.
4.解:(1)因为 CF∥AB,所以∠ADF=∠F,∠A=∠ECF.
在△ADE和△CFE中, 所以△ADE≌△CFE(AAS).
(2)因为△ADE≌△CFE,所以AD=CF=4.
所以BD=AB-AD=5-4=1.
5.解:因为 AD∥EC,所以∠A=∠C.
因为∠DBC+∠ABD=180°,∠DBC+∠BEC=180°,所以∠ABD=∠CEB.
又BD=EB,所以△ADB≌△CBE(AAS).所以AD=BC.
6.解:(1)因为AC平分∠BAD,所以∠BAC=∠DAC.
因为CB⊥AB,CD⊥AD,所以∠B=∠D=90°.
在△ABC和△ADC中, 所以△ABC≌△ADC(AAS).
(2)由(1)知:△ABC≌△ADC,所以
所以 所以
所以
故四边形 ABCD的面积是 12.
7.解:(1)因为 BE平分∠ABC,所以∠ABE=∠DBE.
在△ABE和△DBE中, 所以△ABE≌△DBE(SAS).
(2)因为∠A=100°,∠C=50°,所以∠ABC=30°.
因为BE平分∠ABC,所以
在△ABE中,∠AEB=180°—∠A—∠ABE=180°—100°—15°=65°.
8.解:因为∠BDA=∠BAC=α,所以∠ABD+∠BAD=180°-α=∠BAD+∠CAE.
所以∠ABD=∠CAE.
在△ABD和△CAE中, 所以△ABD≌△CAE(AAS).
所以AD=CE,BD=AE.
因为 CE=a,BD=b,所以DE=AD+AE=CE+BD=a+b.
