1.3 探索三角形全等的条件第4课时 用适当的方法判定三角形全等同步训练(含答案)
文档属性
| 名称 | 1.3 探索三角形全等的条件第4课时 用适当的方法判定三角形全等同步训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-18 22:16:29 | ||
图片预览

文档简介
第一章 三角形
3 探索三角形全等的条件
第4课时 用适当的方法判定三角形全等
基础夯实
知识点一 添加条件判定三角形全等
1.如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A.∠A=∠D B.∠ACB=∠DBC C. AC=DB D. AB=DC
2.如图,AC与BD相交于点 P,AP=CP,从以下四个条件:①AB=CD,②BP=DP,③∠B= ∠D,④∠A=∠C中选择一个作为条件,则不一定能使△APB≌△CPD的是 ______________.(只填序号)
3.如图,在△ABC 和△DEC中,∠BCE=∠ACD,BC=EC.请你添加一个条件,使得△ABC和△DEC全等,并说明理由.
知识点二 全等三角形的性质与判定的综合应用
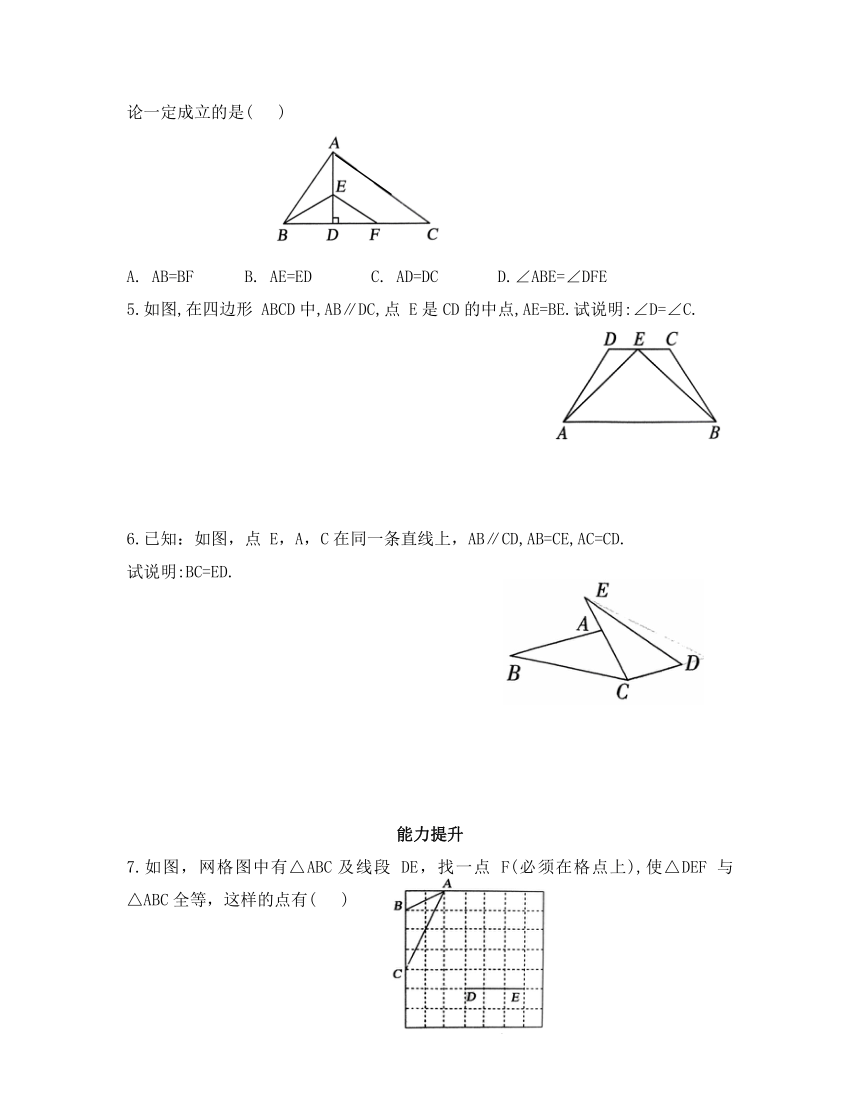
4.如图,在 Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交 AD于点E,EF∥AC.下列结论一定成立的是( )
A. AB=BF B. AE=ED C. AD=DC D.∠ABE=∠DFE
5.如图,在四边形 ABCD中,AB∥DC,点 E是CD的中点,AE=BE.试说明:∠D=∠C.
6.已知:如图,点 E,A,C在同一条直线上,AB∥CD,AB=CE,AC=CD.
试说明:BC=ED.
能力提升
7.如图,网格图中有△ABC及线段 DE,找一点 F(必须在格点上),使△DEF 与 △ABC全等,这样的点有( )
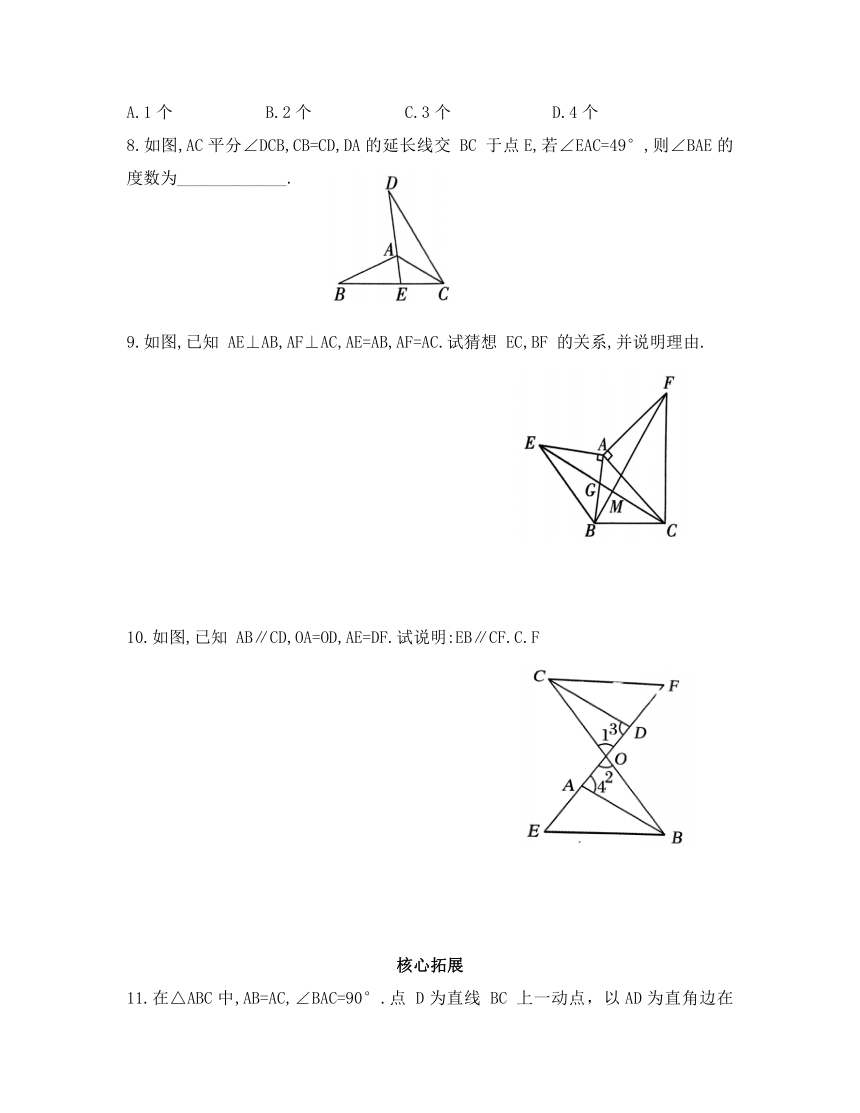
A.1个 B.2个 C.3个 D.4个
8.如图,AC平分∠DCB,CB=CD,DA的延长线交 BC 于点E,若∠EAC=49°,则∠BAE的度数为_____________.
9.如图,已知 AE⊥AB,AF⊥AC,AE=AB,AF=AC.试猜想 EC,BF 的关系,并说明理由.
10.如图,已知 AB∥CD,OA=OD,AE=DF.试说明:EB∥CF.C.F
核心拓展
11.在△ABC中,AB=AC,∠BAC=90°.点 D为直线 BC 上一动点,以AD为直角边在AD的右侧作等腰直角三角形 ADE,使∠DAE=90°,AD=AE.
(1)当点 D在线段 BC 上时,如图1,试说明:△ABD≌△ACE;
(2)当点 D在线段 CB 的延长线上时,如图2,判断 CE与 BC 的位置关系,并说明理由.
参考答案
1. C【解析】因为∠ABC=∠DCB,BC=CB,当∠A=∠D时,根据“AAS”能判断△ABC≌△DCB;当∠ACB=∠DBC时,根据“ASA”能判断△ABC≌△DCB;当AC=DB时,“SSA”不能判断△ABC≌△DCB;当AB=DC时,根据“SAS”能判断△ABC≌△DCB.
2.①
3.解:添加条件 CA=CD.理由如下:
因为∠BCE=∠ACD,所以∠BCE+∠BCD=∠ACD+∠BCD,即∠DCE=∠ACB.
在△ABC 和△DEC中, 所以△ABC≌△DEC(SAS)(答案不唯一).
4. A 【解析】由题意,易知∠EFB=∠C=∠BAD,∠EBF=∠EBA,BE=BE,
所以△EBF≌△EBA(AAS).所以AB=BF.
5.解:因为 AE=BE,所以∠EAB=∠EBA.
因为 AB∥DC,所以∠DEA=∠EAB,∠CEB=∠EBA.所以∠DEA=∠CEB.
因为点 E是CD的中点,所以DE=CE.
在△ADE和△BCE中, 所以△ADE≌△BCE(SAS).
所以∠D=∠C.
6.解:因为AB∥CD,所以∠BAC=∠ECD.
又因为 AB=CE,AC=CD,所以△BCA≌△EDC(SAS),所以 BC=ED.
7. D【解析】如图所示,这样的点有4个.
8.82°【解析】因为 AC平分∠DCB,所以∠BCA=∠DCA.
因为CB=CD,AC=AC,所以△ABC≌△ADC(SAS).所以∠B=∠D.
所以∠B+∠ACB=∠D+∠ACD.因为∠CAE=∠D+∠ACD=49°,所以∠B+∠ACB=49°.
所以∠BAE=180°—∠B—∠ACB—∠CAE=82°.故答案为82°.
9.解:EC=BF,EC⊥BF.理由如下:
因为AE⊥AB,AF⊥AC,所以∠EAB=∠CAF=90°.
所以∠EAB+∠BAC=∠CAF+∠BAC.所以∠EAC=∠BAF.
在△EAC和△BAF中,因为 AE=AB,∠EAC=∠BAF,AC=AF,所以△EAC≌△BAF(SAS).
所以EC=BF,∠AEC=∠ABF.
因为∠AEG+∠AGE=90°,∠AGE=∠BGM,所以∠ABF+∠BGM=90°.所以∠EMB=90°.
所以EC⊥BF.
10.解:(方法一)因为AB∥CD,所以∠3=∠4.
在△ABO和△DCO中, 所以△ABO≌△DCO(ASA).所以OB=OC.
又因为AE=DF,OA=OD,所以OA+AE=OD+DF,即OE=OF.
在△BOE 和△COF 中, 所以△BOE≌△COF(SAS).
所以∠E=∠F.所以EB∥CF.
(方法二)因为 AB∥CD,所以∠3=∠4.
在△ABO和△DCO中, 所以△ABO≌△DCO(ASA).
所以 BA=CD.
因为∠3=∠4,所以∠CDF=∠BAE.
在△CDF和△BAE中, 所以△CDF≌△BAE(SAS).
所以∠F=∠E.
所以EB∥CF.
11.解:(1)因为∠BAC=90°,∠DAE=90°,
所以∠BAD=90°-∠DAC,∠CAE=90°-∠DAC,所以∠BAD=∠CAE.
在△ABD和△ACE中, 所以△ABD≌△ACE(SAS).
(2)CE⊥BC.
理由:因为∠BAC=∠DAE=90°,所以∠BAC-∠BAE=∠DAE-∠BAE,所以∠BAD=∠CAE.
在△DAB与△EAC中, 所以△DAB≌△EAC(SAS).
所以∠ABD=∠ACE.
因为∠ABC=∠ACB=45°,所以∠ABD=∠ACE=135°.
所以∠BCE=∠ACE-∠ACB=135°-45°=90°,即CE⊥BC.
3 探索三角形全等的条件
第4课时 用适当的方法判定三角形全等
基础夯实
知识点一 添加条件判定三角形全等
1.如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A.∠A=∠D B.∠ACB=∠DBC C. AC=DB D. AB=DC
2.如图,AC与BD相交于点 P,AP=CP,从以下四个条件:①AB=CD,②BP=DP,③∠B= ∠D,④∠A=∠C中选择一个作为条件,则不一定能使△APB≌△CPD的是 ______________.(只填序号)
3.如图,在△ABC 和△DEC中,∠BCE=∠ACD,BC=EC.请你添加一个条件,使得△ABC和△DEC全等,并说明理由.
知识点二 全等三角形的性质与判定的综合应用
4.如图,在 Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交 AD于点E,EF∥AC.下列结论一定成立的是( )
A. AB=BF B. AE=ED C. AD=DC D.∠ABE=∠DFE
5.如图,在四边形 ABCD中,AB∥DC,点 E是CD的中点,AE=BE.试说明:∠D=∠C.
6.已知:如图,点 E,A,C在同一条直线上,AB∥CD,AB=CE,AC=CD.
试说明:BC=ED.
能力提升
7.如图,网格图中有△ABC及线段 DE,找一点 F(必须在格点上),使△DEF 与 △ABC全等,这样的点有( )
A.1个 B.2个 C.3个 D.4个
8.如图,AC平分∠DCB,CB=CD,DA的延长线交 BC 于点E,若∠EAC=49°,则∠BAE的度数为_____________.
9.如图,已知 AE⊥AB,AF⊥AC,AE=AB,AF=AC.试猜想 EC,BF 的关系,并说明理由.
10.如图,已知 AB∥CD,OA=OD,AE=DF.试说明:EB∥CF.C.F
核心拓展
11.在△ABC中,AB=AC,∠BAC=90°.点 D为直线 BC 上一动点,以AD为直角边在AD的右侧作等腰直角三角形 ADE,使∠DAE=90°,AD=AE.
(1)当点 D在线段 BC 上时,如图1,试说明:△ABD≌△ACE;
(2)当点 D在线段 CB 的延长线上时,如图2,判断 CE与 BC 的位置关系,并说明理由.
参考答案
1. C【解析】因为∠ABC=∠DCB,BC=CB,当∠A=∠D时,根据“AAS”能判断△ABC≌△DCB;当∠ACB=∠DBC时,根据“ASA”能判断△ABC≌△DCB;当AC=DB时,“SSA”不能判断△ABC≌△DCB;当AB=DC时,根据“SAS”能判断△ABC≌△DCB.
2.①
3.解:添加条件 CA=CD.理由如下:
因为∠BCE=∠ACD,所以∠BCE+∠BCD=∠ACD+∠BCD,即∠DCE=∠ACB.
在△ABC 和△DEC中, 所以△ABC≌△DEC(SAS)(答案不唯一).
4. A 【解析】由题意,易知∠EFB=∠C=∠BAD,∠EBF=∠EBA,BE=BE,
所以△EBF≌△EBA(AAS).所以AB=BF.
5.解:因为 AE=BE,所以∠EAB=∠EBA.
因为 AB∥DC,所以∠DEA=∠EAB,∠CEB=∠EBA.所以∠DEA=∠CEB.
因为点 E是CD的中点,所以DE=CE.
在△ADE和△BCE中, 所以△ADE≌△BCE(SAS).
所以∠D=∠C.
6.解:因为AB∥CD,所以∠BAC=∠ECD.
又因为 AB=CE,AC=CD,所以△BCA≌△EDC(SAS),所以 BC=ED.
7. D【解析】如图所示,这样的点有4个.
8.82°【解析】因为 AC平分∠DCB,所以∠BCA=∠DCA.
因为CB=CD,AC=AC,所以△ABC≌△ADC(SAS).所以∠B=∠D.
所以∠B+∠ACB=∠D+∠ACD.因为∠CAE=∠D+∠ACD=49°,所以∠B+∠ACB=49°.
所以∠BAE=180°—∠B—∠ACB—∠CAE=82°.故答案为82°.
9.解:EC=BF,EC⊥BF.理由如下:
因为AE⊥AB,AF⊥AC,所以∠EAB=∠CAF=90°.
所以∠EAB+∠BAC=∠CAF+∠BAC.所以∠EAC=∠BAF.
在△EAC和△BAF中,因为 AE=AB,∠EAC=∠BAF,AC=AF,所以△EAC≌△BAF(SAS).
所以EC=BF,∠AEC=∠ABF.
因为∠AEG+∠AGE=90°,∠AGE=∠BGM,所以∠ABF+∠BGM=90°.所以∠EMB=90°.
所以EC⊥BF.
10.解:(方法一)因为AB∥CD,所以∠3=∠4.
在△ABO和△DCO中, 所以△ABO≌△DCO(ASA).所以OB=OC.
又因为AE=DF,OA=OD,所以OA+AE=OD+DF,即OE=OF.
在△BOE 和△COF 中, 所以△BOE≌△COF(SAS).
所以∠E=∠F.所以EB∥CF.
(方法二)因为 AB∥CD,所以∠3=∠4.
在△ABO和△DCO中, 所以△ABO≌△DCO(ASA).
所以 BA=CD.
因为∠3=∠4,所以∠CDF=∠BAE.
在△CDF和△BAE中, 所以△CDF≌△BAE(SAS).
所以∠F=∠E.
所以EB∥CF.
11.解:(1)因为∠BAC=90°,∠DAE=90°,
所以∠BAD=90°-∠DAC,∠CAE=90°-∠DAC,所以∠BAD=∠CAE.
在△ABD和△ACE中, 所以△ABD≌△ACE(SAS).
(2)CE⊥BC.
理由:因为∠BAC=∠DAE=90°,所以∠BAC-∠BAE=∠DAE-∠BAE,所以∠BAD=∠CAE.
在△DAB与△EAC中, 所以△DAB≌△EAC(SAS).
所以∠ABD=∠ACE.
因为∠ABC=∠ACB=45°,所以∠ABD=∠ACE=135°.
所以∠BCE=∠ACE-∠ACB=135°-45°=90°,即CE⊥BC.
