1.3正方形的性质与判定 同步练习 2022-2023学年北师大版九年级数学上册(含解析)
文档属性
| 名称 | 1.3正方形的性质与判定 同步练习 2022-2023学年北师大版九年级数学上册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 325.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 16:50:43 | ||
图片预览


文档简介
北师大版九上1.3正方形的性质与判定
(共19题)
一、选择题(共12题)
下列说法:
①四边相等的四边形一定是菱形
②顺次连接矩形各边中点形成的四边形一定是正方形
③对角线相等的四边形一定是矩形
④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分
其中正确的有 个.
A. B. C. D.
正方形的一条对角线长为 ,则这个正方形的面积是
A. B. C. D.
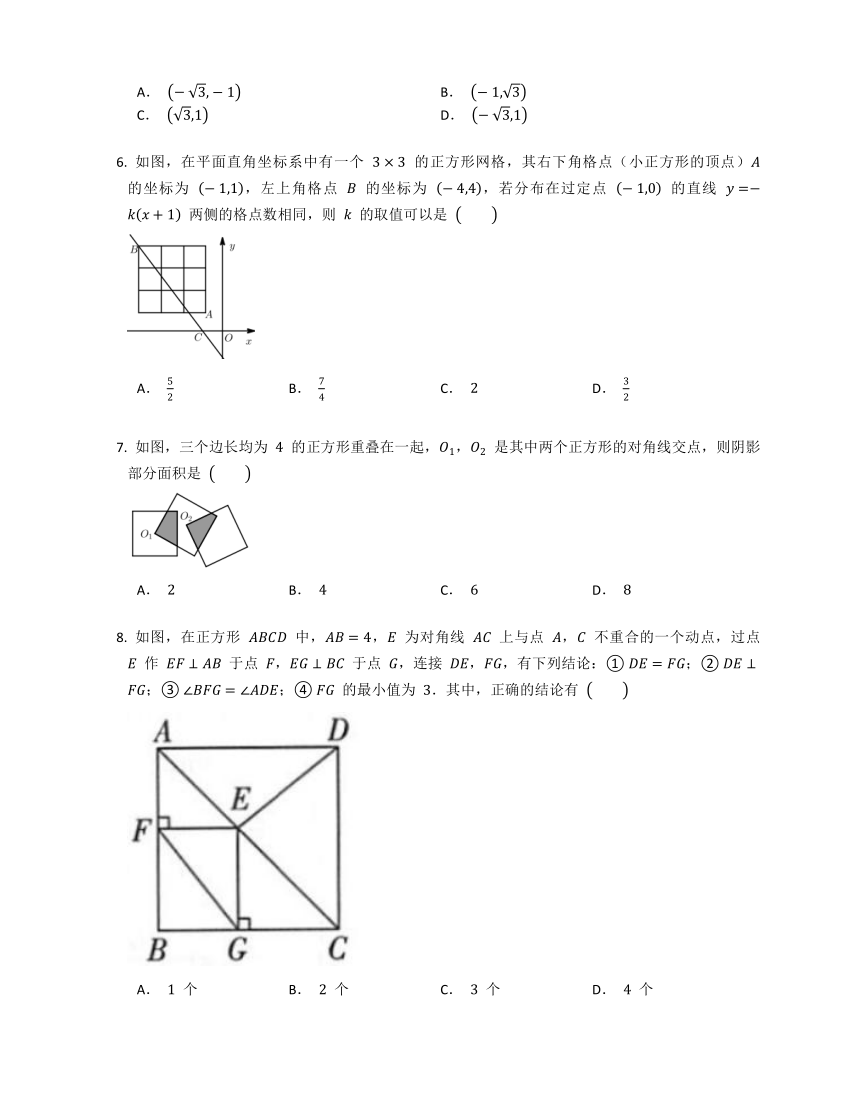
如图,在正方形 中,, 是边 上的一点,.将 沿 对折至 ,连接 ,则 的长为
A. B. C. D.
若正方形的周长为 ,则其对角线长为
A. B. C. D.
如图,将正方形 放在平面直角坐标系中, 是原点, 的坐标为 ,则点 的坐标为
A. B.
C. D.
如图,在平面直角坐标系中有一个 的正方形网格,其右下角格点(小正方形的顶点) 的坐标为 ,左上角格点 的坐标为 ,若分布在过定点 的直线 两侧的格点数相同,则 的取值可以是
A. B. C. D.
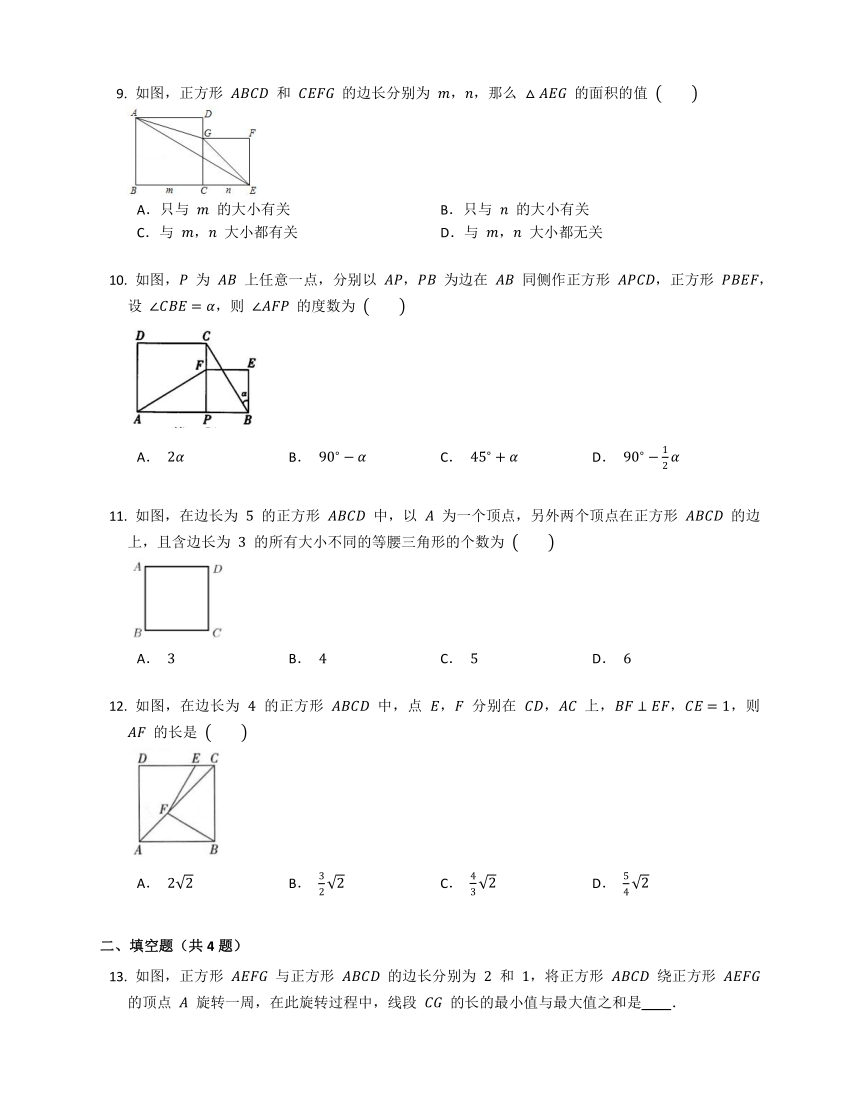
如图,三个边长均为 的正方形重叠在一起,, 是其中两个正方形的对角线交点,则阴影部分面积是
A. B. C. D.
如图,在正方形 中,, 为对角线 上与点 , 不重合的一个动点,过点 作 于点 , 于点 ,连接 ,,有下列结论:① ;② ;③ ;④ 的最小值为 .其中,正确的结论有
A. 个 B. 个 C. 个 D. 个
如图,正方形 和 的边长分别为 ,,那么 的面积的值
A.只与 的大小有关 B.只与 的大小有关
C.与 , 大小都有关 D.与 , 大小都无关
如图, 为 上任意一点,分别以 , 为边在 同侧作正方形 ,正方形 ,设 ,则 的度数为
A. B. C. D.
如图,在边长为 的正方形 中,以 为一个顶点,另外两个顶点在正方形 的边上,且含边长为 的所有大小不同的等腰三角形的个数为
A. B. C. D.
如图,在边长为 的正方形 中,点 , 分别在 , 上,,,则 的长是
A. B. C. D.
二、填空题(共4题)
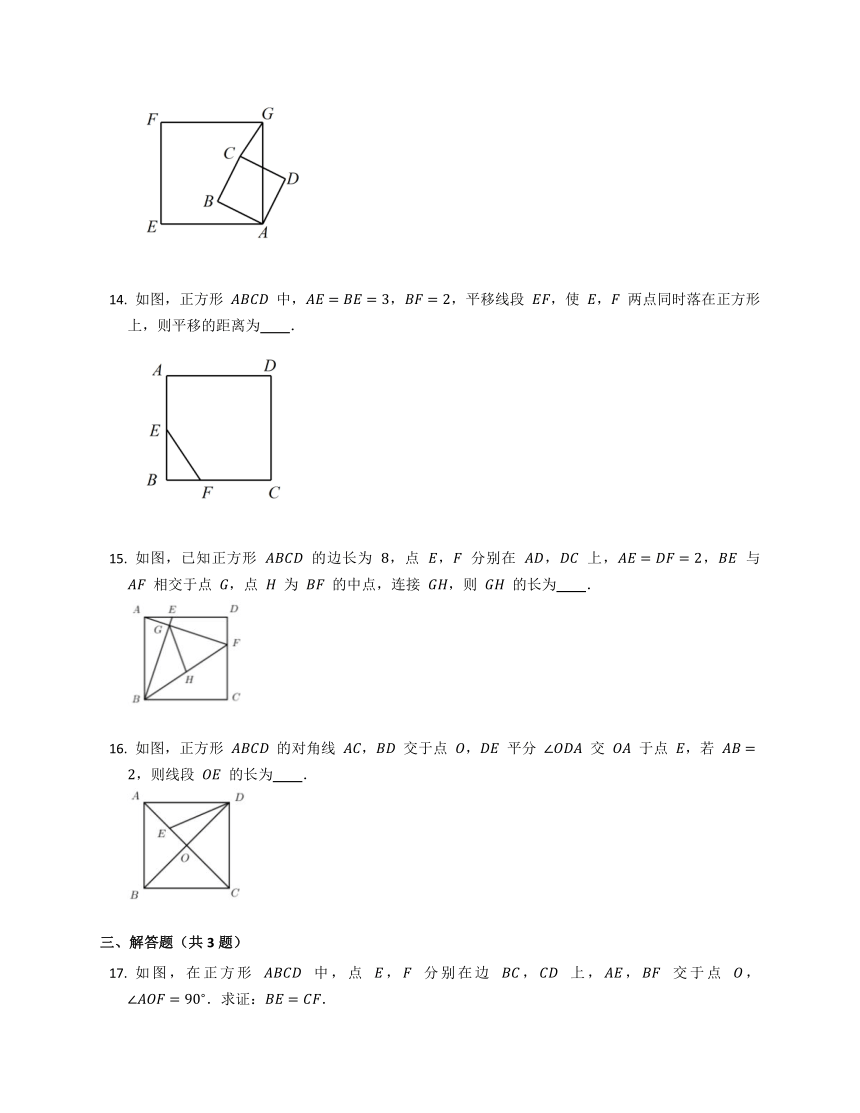
如图,正方形 与正方形 的边长分别为 和 ,将正方形 绕正方形 的顶点 旋转一周,在此旋转过程中,线段 的长的最小值与最大值之和是 .
如图,正方形 中,,,平移线段 ,使 , 两点同时落在正方形上,则平移的距离为 .
如图,已知正方形 的边长为 ,点 , 分别在 , 上,, 与 相交于点 ,点 为 的中点,连接 ,则 的长为 .
如图,正方形 的对角线 , 交于点 , 平分 交 于点 ,若 ,则线段 的长为 .
三、解答题(共3题)
如图,在正方形 中,点 , 分别在边 , 上,, 交于点 ,.求证:.
如图 ,在正方形 中, 是 上一点, 是 延长线上一点,且 .易证:.
(1) 在图 中,若 在 上,且 .试猜想 ,, 三线段之间的数量关系,并证明你的结论.
(2) 运用()中解答所积累的经验和知识,完成下面两题:
①如图 ,在四边形 中 ,,点 ,点 分别是 边, 边上的动点.若 ,,试探索当 和 满足什么关系时,图 中 ,, 三线段之间的关系仍然成立,并说明理由.
②在平面直角坐标中,边长为 的正方形 的两顶点 , 分别在 轴、 轴的正半轴上,点 在原点.现将正方形 绕 点顺时针旋转,当 点第一次落在直线 上时停止旋转,旋转过程中, 边交直线 于点 , 边交 轴于点 (如图 ).设 的周长为 ,在旋转正方形 的过程中, 值是否有变化?若不变,请直接写出结论.
如图 ,正方形 的边长为 ,点 从点 出发,沿射线 方向以 /秒的速度移动,点 从点 出发,向点 以 /秒的速度移动(不到点 ).设点 , 同时出发移动 秒.
(1) 在点 , 移动过程中,连接 ,,,则 的形状是 ,始终保持不变;
(2) 如图 ,连接 ,设 交 移动 ,当 时,求 的长;
(3) 如图 ,点 , 分别在边 , 上,且 ,连接 ,当 与 的夹角为 ,求 的值.
答案
一、选择题(共12题)
1. 【答案】C
【解析】 四边相等的四边形一定是菱形,
①正确;
顺次连接矩形各边中点形成的四边形一定是菱形,
②错误;
对角线相等的平行四边形才是矩形,
③错误;
经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分,
④正确.
其中正确的有 个.
2. 【答案】A
【解析】 正方形的一条对角线长为 ,
这个正方形的面积 .
3. 【答案】D
4. 【答案】C
5. 【答案】D
【解析】如图所示,过点 作 轴于 ,过点 作 轴于 ,
则 ,
.
点 的坐标为 ,
,.
四边形 是正方形,
,.
又 .
.
在 和 中,
,.
点 在第二象限,
点 的坐标为 .
6. 【答案】B
【解析】 直线 过定点 ,分布在直线 两侧的格点数相同,
由正方形的对称性可知,直线 两侧的格点数相同,
在直线 和直线 之间,两侧格点相同(如图),
,,
,则 .
7. 【答案】D
【解析】连接 ,,如图:
,,
,
四边形 是正方形,
,
在 和 中,
,
, 两个正方形阴影部分的面积是 正方形,
同理另外两个正方形阴影部分的面积也是 正方形,
.
8. 【答案】C
9. 【答案】B
【解析】 的面积是 .
四边形 是直角梯形,面积是 ;
的面积是:
.
10. 【答案】B
11. 【答案】C
【解析】满足条件的所有图形如图所示:
共 个.
故选C.
12. 【答案】B
二、填空题(共4题)
13. 【答案】
14. 【答案】
15. 【答案】
【解析】 四边形 为正方形,
,,
在 和 中,
(),
,
,
,
,
点 为 的中点,
,
,,
,
.
16. 【答案】
【解析】 四边形 是正方形,
,,,,
平分 ,
,
,
,
,
,
,,
,
,
.
三、解答题(共3题)
17. 【答案】 四边形 是正方形,
,,
,,
,
又 ,
(同角的余角相等),
在 和 中,
,
.
18. 【答案】
(1) ,理由如下:
四边形 是正方形, 是 延长线上一点,
,,
在 和 中,
,
,,
,
,
,
,
在 和 中,
,
,
.
(2) ① 时,;理由如下:
延长 到 点,使 ,连接 ,如图()所示:
,
在 和 中,
,
,,
,
当 时,,
在 和 中,
,
,
;
②在旋转正方形 的过程中, 值无变化;
【解析】
(2) 延长 交 轴于 点,如图()所示:
则 ,,
.
又 ,.
在 和 中,
.
,.
在 和 中,
.
.
,
.
在旋转正方形 的过程中, 值无变化.
19. 【答案】
(1) 等腰直角三角形
(2) 如图 ,过点 作 ,交 于点 ,
则 .
所以 ,
所以 .
在 与 中,
所以 ,
所以 .
因为 中,,,
所以 ,
所以 .
(3) 如图 ,连接 ,,
设 与 交于 .
由()得 ,又 ,
所以 ,
又因为 ,
所以四边形 是平行四边形,
所以 ,
在 中,得 ,
所以 .
【解析】
(1) 等腰直角三角形.理由如下:
如图 ,
在正方形 中,,.
依题意得:.
在 与 中,
所以 ,
所以 ,,
所以 ,
所以 是等腰直角三角形.
(共19题)
一、选择题(共12题)
下列说法:
①四边相等的四边形一定是菱形
②顺次连接矩形各边中点形成的四边形一定是正方形
③对角线相等的四边形一定是矩形
④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分
其中正确的有 个.
A. B. C. D.
正方形的一条对角线长为 ,则这个正方形的面积是
A. B. C. D.
如图,在正方形 中,, 是边 上的一点,.将 沿 对折至 ,连接 ,则 的长为
A. B. C. D.
若正方形的周长为 ,则其对角线长为
A. B. C. D.
如图,将正方形 放在平面直角坐标系中, 是原点, 的坐标为 ,则点 的坐标为
A. B.
C. D.
如图,在平面直角坐标系中有一个 的正方形网格,其右下角格点(小正方形的顶点) 的坐标为 ,左上角格点 的坐标为 ,若分布在过定点 的直线 两侧的格点数相同,则 的取值可以是
A. B. C. D.
如图,三个边长均为 的正方形重叠在一起,, 是其中两个正方形的对角线交点,则阴影部分面积是
A. B. C. D.
如图,在正方形 中,, 为对角线 上与点 , 不重合的一个动点,过点 作 于点 , 于点 ,连接 ,,有下列结论:① ;② ;③ ;④ 的最小值为 .其中,正确的结论有
A. 个 B. 个 C. 个 D. 个
如图,正方形 和 的边长分别为 ,,那么 的面积的值
A.只与 的大小有关 B.只与 的大小有关
C.与 , 大小都有关 D.与 , 大小都无关
如图, 为 上任意一点,分别以 , 为边在 同侧作正方形 ,正方形 ,设 ,则 的度数为
A. B. C. D.
如图,在边长为 的正方形 中,以 为一个顶点,另外两个顶点在正方形 的边上,且含边长为 的所有大小不同的等腰三角形的个数为
A. B. C. D.
如图,在边长为 的正方形 中,点 , 分别在 , 上,,,则 的长是
A. B. C. D.
二、填空题(共4题)
如图,正方形 与正方形 的边长分别为 和 ,将正方形 绕正方形 的顶点 旋转一周,在此旋转过程中,线段 的长的最小值与最大值之和是 .
如图,正方形 中,,,平移线段 ,使 , 两点同时落在正方形上,则平移的距离为 .
如图,已知正方形 的边长为 ,点 , 分别在 , 上,, 与 相交于点 ,点 为 的中点,连接 ,则 的长为 .
如图,正方形 的对角线 , 交于点 , 平分 交 于点 ,若 ,则线段 的长为 .
三、解答题(共3题)
如图,在正方形 中,点 , 分别在边 , 上,, 交于点 ,.求证:.
如图 ,在正方形 中, 是 上一点, 是 延长线上一点,且 .易证:.
(1) 在图 中,若 在 上,且 .试猜想 ,, 三线段之间的数量关系,并证明你的结论.
(2) 运用()中解答所积累的经验和知识,完成下面两题:
①如图 ,在四边形 中 ,,点 ,点 分别是 边, 边上的动点.若 ,,试探索当 和 满足什么关系时,图 中 ,, 三线段之间的关系仍然成立,并说明理由.
②在平面直角坐标中,边长为 的正方形 的两顶点 , 分别在 轴、 轴的正半轴上,点 在原点.现将正方形 绕 点顺时针旋转,当 点第一次落在直线 上时停止旋转,旋转过程中, 边交直线 于点 , 边交 轴于点 (如图 ).设 的周长为 ,在旋转正方形 的过程中, 值是否有变化?若不变,请直接写出结论.
如图 ,正方形 的边长为 ,点 从点 出发,沿射线 方向以 /秒的速度移动,点 从点 出发,向点 以 /秒的速度移动(不到点 ).设点 , 同时出发移动 秒.
(1) 在点 , 移动过程中,连接 ,,,则 的形状是 ,始终保持不变;
(2) 如图 ,连接 ,设 交 移动 ,当 时,求 的长;
(3) 如图 ,点 , 分别在边 , 上,且 ,连接 ,当 与 的夹角为 ,求 的值.
答案
一、选择题(共12题)
1. 【答案】C
【解析】 四边相等的四边形一定是菱形,
①正确;
顺次连接矩形各边中点形成的四边形一定是菱形,
②错误;
对角线相等的平行四边形才是矩形,
③错误;
经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分,
④正确.
其中正确的有 个.
2. 【答案】A
【解析】 正方形的一条对角线长为 ,
这个正方形的面积 .
3. 【答案】D
4. 【答案】C
5. 【答案】D
【解析】如图所示,过点 作 轴于 ,过点 作 轴于 ,
则 ,
.
点 的坐标为 ,
,.
四边形 是正方形,
,.
又 .
.
在 和 中,
,.
点 在第二象限,
点 的坐标为 .
6. 【答案】B
【解析】 直线 过定点 ,分布在直线 两侧的格点数相同,
由正方形的对称性可知,直线 两侧的格点数相同,
在直线 和直线 之间,两侧格点相同(如图),
,,
,则 .
7. 【答案】D
【解析】连接 ,,如图:
,,
,
四边形 是正方形,
,
在 和 中,
,
, 两个正方形阴影部分的面积是 正方形,
同理另外两个正方形阴影部分的面积也是 正方形,
.
8. 【答案】C
9. 【答案】B
【解析】 的面积是 .
四边形 是直角梯形,面积是 ;
的面积是:
.
10. 【答案】B
11. 【答案】C
【解析】满足条件的所有图形如图所示:
共 个.
故选C.
12. 【答案】B
二、填空题(共4题)
13. 【答案】
14. 【答案】
15. 【答案】
【解析】 四边形 为正方形,
,,
在 和 中,
(),
,
,
,
,
点 为 的中点,
,
,,
,
.
16. 【答案】
【解析】 四边形 是正方形,
,,,,
平分 ,
,
,
,
,
,
,,
,
,
.
三、解答题(共3题)
17. 【答案】 四边形 是正方形,
,,
,,
,
又 ,
(同角的余角相等),
在 和 中,
,
.
18. 【答案】
(1) ,理由如下:
四边形 是正方形, 是 延长线上一点,
,,
在 和 中,
,
,,
,
,
,
,
在 和 中,
,
,
.
(2) ① 时,;理由如下:
延长 到 点,使 ,连接 ,如图()所示:
,
在 和 中,
,
,,
,
当 时,,
在 和 中,
,
,
;
②在旋转正方形 的过程中, 值无变化;
【解析】
(2) 延长 交 轴于 点,如图()所示:
则 ,,
.
又 ,.
在 和 中,
.
,.
在 和 中,
.
.
,
.
在旋转正方形 的过程中, 值无变化.
19. 【答案】
(1) 等腰直角三角形
(2) 如图 ,过点 作 ,交 于点 ,
则 .
所以 ,
所以 .
在 与 中,
所以 ,
所以 .
因为 中,,,
所以 ,
所以 .
(3) 如图 ,连接 ,,
设 与 交于 .
由()得 ,又 ,
所以 ,
又因为 ,
所以四边形 是平行四边形,
所以 ,
在 中,得 ,
所以 .
【解析】
(1) 等腰直角三角形.理由如下:
如图 ,
在正方形 中,,.
依题意得:.
在 与 中,
所以 ,
所以 ,,
所以 ,
所以 是等腰直角三角形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
