北师大版数学九年级上册4.7相似三角形的性质 教学课件(共16张PPT)
文档属性
| 名称 | 北师大版数学九年级上册4.7相似三角形的性质 教学课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 351.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 22:12:00 | ||
图片预览



文档简介
(共16张PPT)
第四章 图形的相似
4.7 相似三角形的性质
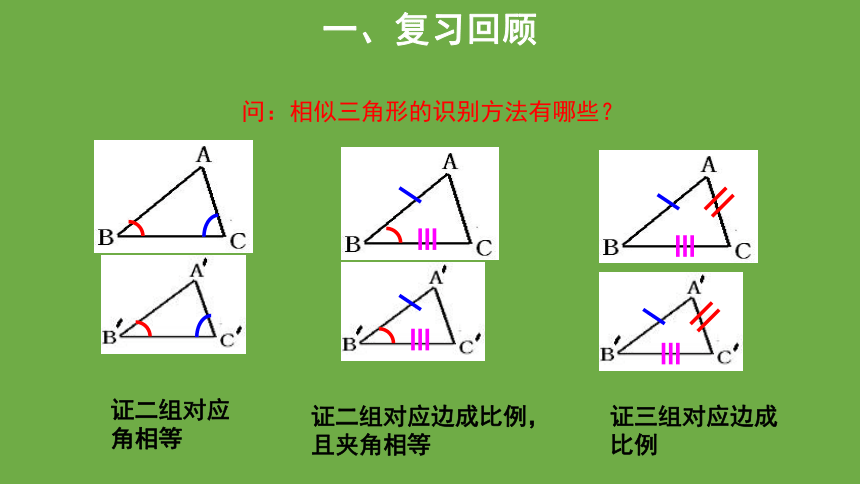
问:相似三角形的识别方法有哪些?
证二组对应角相等
证三组对应边成比例
证二组对应边成比例,且夹角相等
一、复习回顾
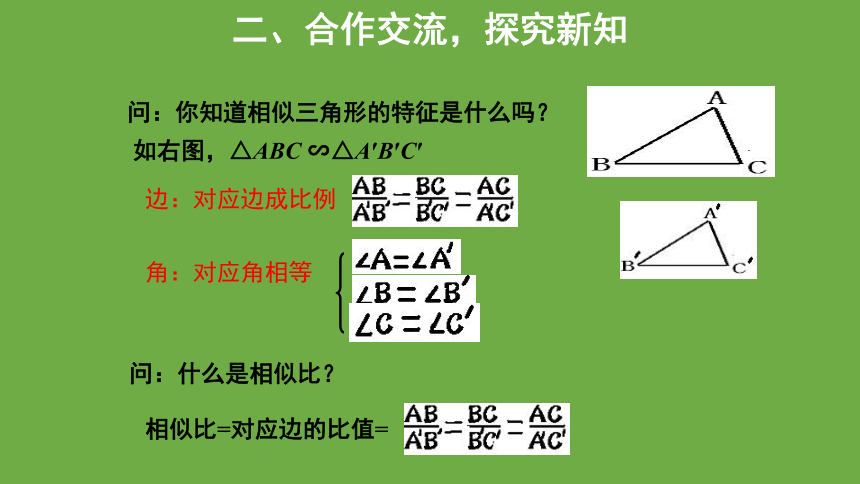
问:你知道相似三角形的特征是什么吗?
角:对应角相等
边:对应边成比例
问:什么是相似比?
相似比=对应边的比值=
如右图,△ABC ∽△A′B′C′
二、合作交流,探究新知
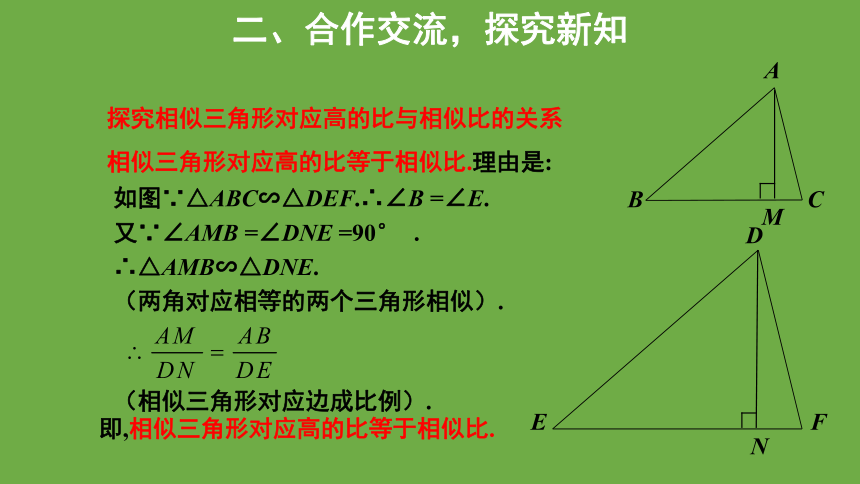
探究相似三角形对应高的比与相似比的关系
如图∵△ABC∽△DEF.∴∠B =∠E.
又∵∠AMB =∠DNE =90° .
∴△AMB∽△DNE.
(两角对应相等的两个三角形相似).
相似三角形对应高的比等于相似比.理由是:
(相似三角形对应边成比例).
A
B
C
M
D
E
F
N
即,相似三角形对应高的比等于相似比.
二、合作交流,探究新知
探究相似三角形对应角平分线的比与相似比的关系
如图∵△ABC∽△DEF.∴∠B =∠E, ∠BAC=∠EDF.
又∵AM,DN分别是∠BAC和∠EDF的角平分线.
∴∠BAM=∠EDN.
∴△AMB∽△DNE.
(两角对应相等的两个三角形相似)
相似三角形对应角平分线的比等于相似比.理由是:
(相似三角形对应边成比例)
即:相似三角形对应角平分线的比等于相似比.
二、合作交流,探究新知
探究相似三角形对应中线的比与相似比的关系
如图∵△ABC∽△DEF.
∴∠B =∠E,
相似三角形对应中线的比等于相似比.理由是:
(相似三角形对应边成比例)
又∵AM, DN分别是△ABC和△DEF的中线.
∴△AMB∽△DNE(两边对应成比例且夹角相等的两个三角形相似)
且∠B =∠E.
即:相似三角形对应中线的比等于相似比.
二、合作交流,探究新知
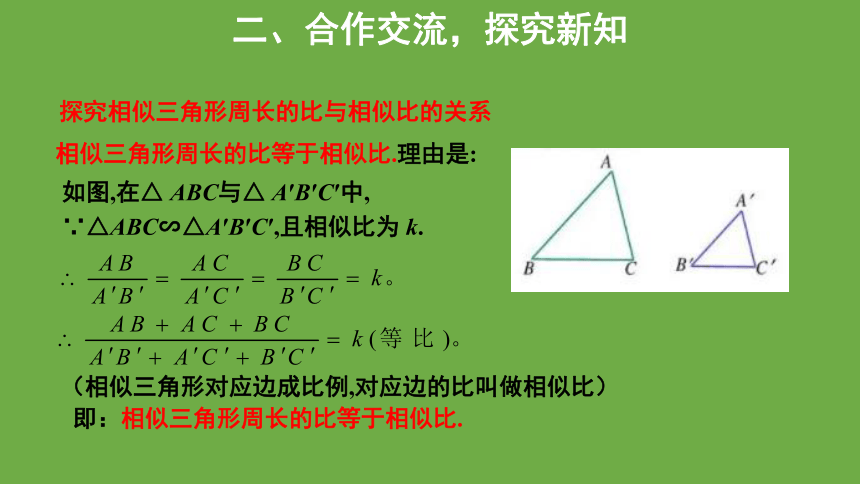
探究相似三角形周长的比与相似比的关系
如图,在△ ABC与△ A′B′C′中,
∵△ABC∽△A′B′C′,且相似比为 k.
相似三角形周长的比等于相似比.理由是:
(相似三角形对应边成比例,对应边的比叫做相似比)
即:相似三角形周长的比等于相似比.
二、合作交流,探究新知
三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形.
相似三角形的各对应角相等,各对应边对应成比例.
相似三角形对应高的比,对应角平分线的比,对应中线的比,对应周长的
比等于相似比.
相似比等于 1 的两个三角形全等.
注意:
要把表示对应角顶点的字母写在对应的位置上.
反之,写在对应位置上的字母就是对应角的顶点.
由于相似三角形与其位置无关,因此,能否弄清对应是正确解答的前提和关键.
二、合作交流,探究新知
判定两个三角形相似的方法:
两角对应相等的两个三角形相似.
三边对应成比例的两个三角形相似.
两边对应成比例,且夹角相等的两个三角形相似.
斜边直角边对应成比例的两个三角形相似.
平行于三角形一边的直线截其它两边(或其延长线),所截得的三角形与原三角形相似.
A
B
C
D
E
A
D
E
B
C
E
D
C
B
A
二、合作交流,探究新知
结论1: 平行于三角形一边直线截其它两边(或其延长线),所截得的三角形与原三角形相似;
如图, 已知△ABC, DE ∥ BC, 交AB,AC或其延长线于D,E,则有如下结论:
A
B
C
D
E
如图: 在△ABC中,
如果DE∥BC,那么△ADE∽△ABC.
结论2: 平行于三角形一边直线截其它两边(或其延长线),所得的对应线段成比例.
如图: 在△ABC中,如果DE∥BC,
A
D
E
B
C
E
D
C
B
A
二、合作交流,探究新知
三、运用新知
1. 如图所示,在等腰△ABC 中,底边 BC = 60 cm, AD = 40 cm, 四边形PQRS是正方形.
(1)△ASR与△ABC相似吗 为什么
(2)求正方形PQRSR的边长.
解:(1) △ASR∽△ABC.理由是:
四边形PQRS是正方形
RS∥BC
∠ASR= ∠B
∠ARS= ∠C
△ASR∽△ABC.
A
B
C
S
R
E
P
D
Q
三、运用新知
(2)由(1)可知, △ASR ∽ △ABC.
设正方形 PQRS 的边长为 x cm, 则 AE =(40 - x)cm,
解得, x = 24.
所以正方形 PQRS 的边长为 24 cm.
(相似三角形对应高的比等于相似比)
(2)求正方形PQRSR的边长.
三、运用新知
2. 问题:
△ABC∽△A′B′C′,它们面积的比与相似比有什么关系
如图, △ABC∽△A′B′C′,相似比是k(如4∶3).
(1)△ABC与△A′B′C′的面积如何表示
(2)△ABC与△A′B′C面积的比是多少
解:(1)分别作高CD,C′D′,则
如果两个相似三角形的相似比是 k ,通过上面的活动,你得出了什么结论
三、运用新知
相似三角形面积的比等于相似比的平方.
如图,如果△ABC∽△A′B′C′,且
这个结论在今后的学习中作用很大,若能理解运用,则受益非浅.
相似多边形的性质:
相似三角形对应高的比,对应角平分线的比,
对应中线的比,对应周长的比都等于相似比.
相似三角形面积的比等于相似比的平方.
四、归纳小结
再 见
第四章 图形的相似
4.7 相似三角形的性质
问:相似三角形的识别方法有哪些?
证二组对应角相等
证三组对应边成比例
证二组对应边成比例,且夹角相等
一、复习回顾
问:你知道相似三角形的特征是什么吗?
角:对应角相等
边:对应边成比例
问:什么是相似比?
相似比=对应边的比值=
如右图,△ABC ∽△A′B′C′
二、合作交流,探究新知
探究相似三角形对应高的比与相似比的关系
如图∵△ABC∽△DEF.∴∠B =∠E.
又∵∠AMB =∠DNE =90° .
∴△AMB∽△DNE.
(两角对应相等的两个三角形相似).
相似三角形对应高的比等于相似比.理由是:
(相似三角形对应边成比例).
A
B
C
M
D
E
F
N
即,相似三角形对应高的比等于相似比.
二、合作交流,探究新知
探究相似三角形对应角平分线的比与相似比的关系
如图∵△ABC∽△DEF.∴∠B =∠E, ∠BAC=∠EDF.
又∵AM,DN分别是∠BAC和∠EDF的角平分线.
∴∠BAM=∠EDN.
∴△AMB∽△DNE.
(两角对应相等的两个三角形相似)
相似三角形对应角平分线的比等于相似比.理由是:
(相似三角形对应边成比例)
即:相似三角形对应角平分线的比等于相似比.
二、合作交流,探究新知
探究相似三角形对应中线的比与相似比的关系
如图∵△ABC∽△DEF.
∴∠B =∠E,
相似三角形对应中线的比等于相似比.理由是:
(相似三角形对应边成比例)
又∵AM, DN分别是△ABC和△DEF的中线.
∴△AMB∽△DNE(两边对应成比例且夹角相等的两个三角形相似)
且∠B =∠E.
即:相似三角形对应中线的比等于相似比.
二、合作交流,探究新知
探究相似三角形周长的比与相似比的关系
如图,在△ ABC与△ A′B′C′中,
∵△ABC∽△A′B′C′,且相似比为 k.
相似三角形周长的比等于相似比.理由是:
(相似三角形对应边成比例,对应边的比叫做相似比)
即:相似三角形周长的比等于相似比.
二、合作交流,探究新知
三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形.
相似三角形的各对应角相等,各对应边对应成比例.
相似三角形对应高的比,对应角平分线的比,对应中线的比,对应周长的
比等于相似比.
相似比等于 1 的两个三角形全等.
注意:
要把表示对应角顶点的字母写在对应的位置上.
反之,写在对应位置上的字母就是对应角的顶点.
由于相似三角形与其位置无关,因此,能否弄清对应是正确解答的前提和关键.
二、合作交流,探究新知
判定两个三角形相似的方法:
两角对应相等的两个三角形相似.
三边对应成比例的两个三角形相似.
两边对应成比例,且夹角相等的两个三角形相似.
斜边直角边对应成比例的两个三角形相似.
平行于三角形一边的直线截其它两边(或其延长线),所截得的三角形与原三角形相似.
A
B
C
D
E
A
D
E
B
C
E
D
C
B
A
二、合作交流,探究新知
结论1: 平行于三角形一边直线截其它两边(或其延长线),所截得的三角形与原三角形相似;
如图, 已知△ABC, DE ∥ BC, 交AB,AC或其延长线于D,E,则有如下结论:
A
B
C
D
E
如图: 在△ABC中,
如果DE∥BC,那么△ADE∽△ABC.
结论2: 平行于三角形一边直线截其它两边(或其延长线),所得的对应线段成比例.
如图: 在△ABC中,如果DE∥BC,
A
D
E
B
C
E
D
C
B
A
二、合作交流,探究新知
三、运用新知
1. 如图所示,在等腰△ABC 中,底边 BC = 60 cm, AD = 40 cm, 四边形PQRS是正方形.
(1)△ASR与△ABC相似吗 为什么
(2)求正方形PQRSR的边长.
解:(1) △ASR∽△ABC.理由是:
四边形PQRS是正方形
RS∥BC
∠ASR= ∠B
∠ARS= ∠C
△ASR∽△ABC.
A
B
C
S
R
E
P
D
Q
三、运用新知
(2)由(1)可知, △ASR ∽ △ABC.
设正方形 PQRS 的边长为 x cm, 则 AE =(40 - x)cm,
解得, x = 24.
所以正方形 PQRS 的边长为 24 cm.
(相似三角形对应高的比等于相似比)
(2)求正方形PQRSR的边长.
三、运用新知
2. 问题:
△ABC∽△A′B′C′,它们面积的比与相似比有什么关系
如图, △ABC∽△A′B′C′,相似比是k(如4∶3).
(1)△ABC与△A′B′C′的面积如何表示
(2)△ABC与△A′B′C面积的比是多少
解:(1)分别作高CD,C′D′,则
如果两个相似三角形的相似比是 k ,通过上面的活动,你得出了什么结论
三、运用新知
相似三角形面积的比等于相似比的平方.
如图,如果△ABC∽△A′B′C′,且
这个结论在今后的学习中作用很大,若能理解运用,则受益非浅.
相似多边形的性质:
相似三角形对应高的比,对应角平分线的比,
对应中线的比,对应周长的比都等于相似比.
相似三角形面积的比等于相似比的平方.
四、归纳小结
再 见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
