北师大版数学九年级上册4.5相似三角形判定定理的证明 教学课件 (共13张PPT)
文档属性
| 名称 | 北师大版数学九年级上册4.5相似三角形判定定理的证明 教学课件 (共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 251.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 22:13:20 | ||
图片预览



文档简介
(共13张PPT)
第四章 图形的相似
4.5 相似三角形判断定理
的证明
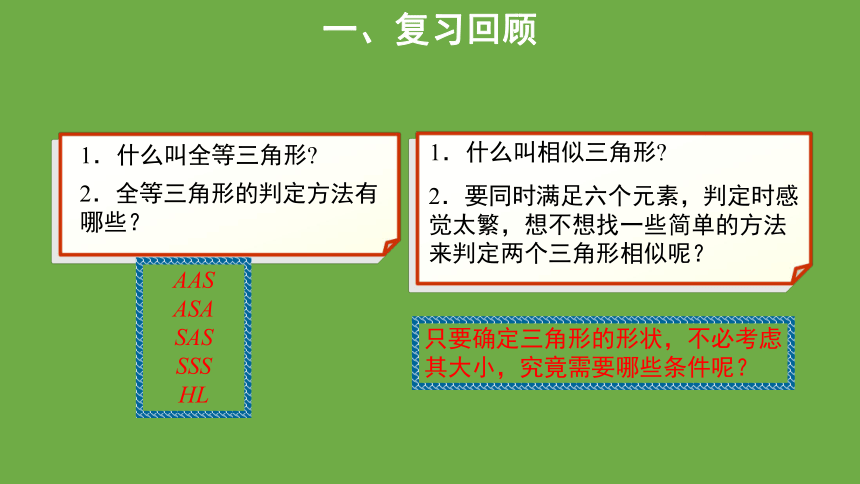
2.全等三角形的判定方法有哪些?
1.什么叫全等三角形
1.什么叫相似三角形
2.要同时满足六个元素,判定时感觉太繁,想不想找一些简单的方法来判定两个三角形相似呢?
AAS
ASA
SAS
SSS
HL
只要确定三角形的形状,不必考虑其大小,究竟需要哪些条件呢?
一、复习回顾
一、复习回顾
判定两个三角形相似的方法有哪些?
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.可以简单说成: 两角对应相等,两三角形相似.
判定定理2:如果一个三角形的三条边与另一个三角形的三条边都对应成比例,那么这两个三角形相似.
判定定理3:如果一个三角形的一个角与另一个三角形的一个角对应相等,并且夹这个相等角的两条边对应成比例,那么这两个三角形相似.
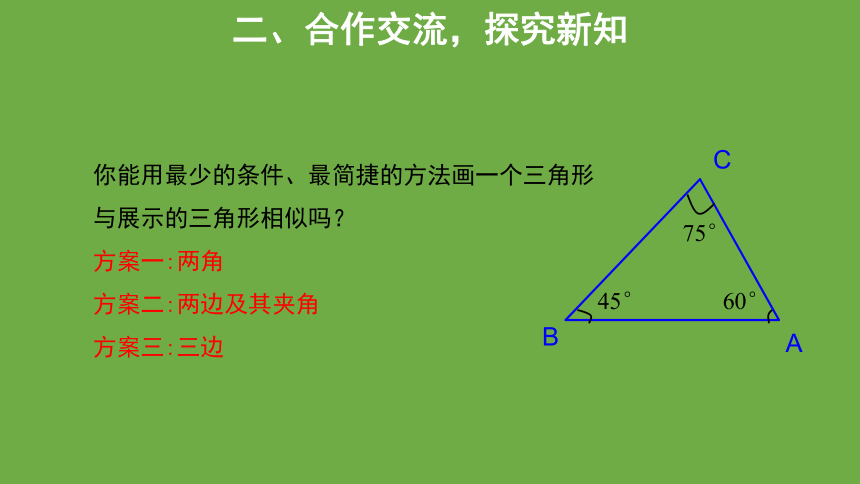
你能用最少的条件、最简捷的方法画一个三角形与展示的三角形相似吗?
方案一:两角
方案二:两边及其夹角
方案三:三边
60°
45°
75°
二、合作交流,探究新知
探索一下:如何证明这些判定定义呢?
1.(AA)判定定理:两角分别相等的两三角形相似.
已知:在ΔABC 和 ΔA'B'C'中,
求证:ΔABC ∽ ΔA'B'C'.
二、合作交流,探究新知
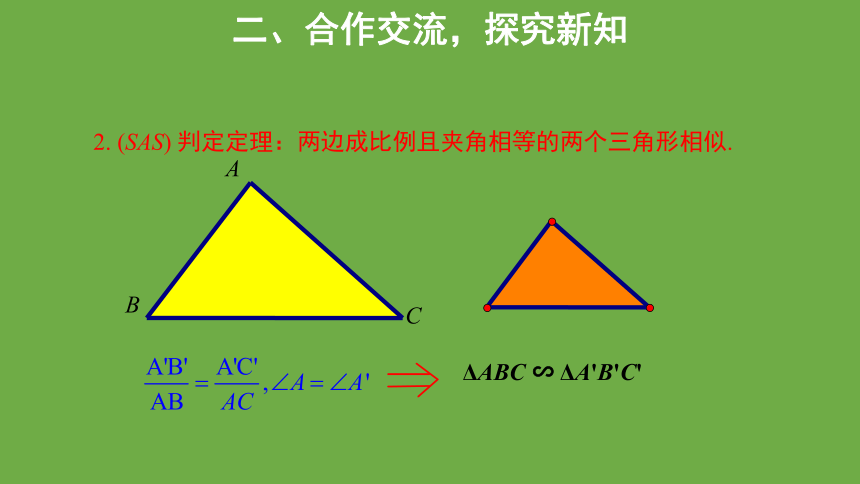
2. (SAS) 判定定理:两边成比例且夹角相等的两个三角形相似.
A
B
C
ΔABC ∽ ΔA'B'C'
二、合作交流,探究新知
求证: △
∽△
A
B
C
D
E
∽
∴
又
∴
∴
∴
∽
∴
二、合作交流,探究新知
A
B
C
∽
(SSS)定理:三边成比例的两个三角形相似.
二、合作交流,探究新知
求证: △
∽△
A
B
C
D
E
∽
∴
又
∴
同理
∴
∴
∴
∽
二、合作交流,探究新知
解:(1)DE // BC
∠ADE 与∠ABC是同位角 ∠AED与∠ACB是同位角
∠ADE =∠ABC,∠AED = ∠ACB
1. 如图, D,E 分别是边 AB,AC 上的点, DE∥BC.
(1)图中有哪些相等的角?
(2)找出图中的相似三角形,并说明理由.
(3)写出图中成比例的线段.
学以致用
三、运用新知
(2)△ADE∽△ABC
∠ADE =∠ABC ∠AED=∠ACB
△ADE∽△ABC
(3)△ADE∽△ABC
=
=
三、运用新知
三角分别相等, 三边成比例
1. 两角分别相等
3. 两边成比例且夹角相等
2. 三边成比例
4. 两边成比例且其中一边的对角相等
四、归纳小结
再 见
第四章 图形的相似
4.5 相似三角形判断定理
的证明
2.全等三角形的判定方法有哪些?
1.什么叫全等三角形
1.什么叫相似三角形
2.要同时满足六个元素,判定时感觉太繁,想不想找一些简单的方法来判定两个三角形相似呢?
AAS
ASA
SAS
SSS
HL
只要确定三角形的形状,不必考虑其大小,究竟需要哪些条件呢?
一、复习回顾
一、复习回顾
判定两个三角形相似的方法有哪些?
判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.可以简单说成: 两角对应相等,两三角形相似.
判定定理2:如果一个三角形的三条边与另一个三角形的三条边都对应成比例,那么这两个三角形相似.
判定定理3:如果一个三角形的一个角与另一个三角形的一个角对应相等,并且夹这个相等角的两条边对应成比例,那么这两个三角形相似.
你能用最少的条件、最简捷的方法画一个三角形与展示的三角形相似吗?
方案一:两角
方案二:两边及其夹角
方案三:三边
60°
45°
75°
二、合作交流,探究新知
探索一下:如何证明这些判定定义呢?
1.(AA)判定定理:两角分别相等的两三角形相似.
已知:在ΔABC 和 ΔA'B'C'中,
求证:ΔABC ∽ ΔA'B'C'.
二、合作交流,探究新知
2. (SAS) 判定定理:两边成比例且夹角相等的两个三角形相似.
A
B
C
ΔABC ∽ ΔA'B'C'
二、合作交流,探究新知
求证: △
∽△
A
B
C
D
E
∽
∴
又
∴
∴
∴
∽
∴
二、合作交流,探究新知
A
B
C
∽
(SSS)定理:三边成比例的两个三角形相似.
二、合作交流,探究新知
求证: △
∽△
A
B
C
D
E
∽
∴
又
∴
同理
∴
∴
∴
∽
二、合作交流,探究新知
解:(1)DE // BC
∠ADE 与∠ABC是同位角 ∠AED与∠ACB是同位角
∠ADE =∠ABC,∠AED = ∠ACB
1. 如图, D,E 分别是边 AB,AC 上的点, DE∥BC.
(1)图中有哪些相等的角?
(2)找出图中的相似三角形,并说明理由.
(3)写出图中成比例的线段.
学以致用
三、运用新知
(2)△ADE∽△ABC
∠ADE =∠ABC ∠AED=∠ACB
△ADE∽△ABC
(3)△ADE∽△ABC
=
=
三、运用新知
三角分别相等, 三边成比例
1. 两角分别相等
3. 两边成比例且夹角相等
2. 三边成比例
4. 两边成比例且其中一边的对角相等
四、归纳小结
再 见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
