带电粒子在有界磁场中的运动 课件 高中物理选择性必修第二册(共21张PPT)
文档属性
| 名称 | 带电粒子在有界磁场中的运动 课件 高中物理选择性必修第二册(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-07-18 22:35:53 | ||
图片预览




文档简介
(共21张PPT)
1.2带电粒子在有界磁场中的运动
回顾:做匀速圆周运动的半径和周期
(1)轨道半径
做由于洛伦兹力提供向心力,则有 ,得到轨道半径为 ,粒子的轨道半径与粒子的速率成正比。
(2)周期
由轨道半径与周期之间的关系知 (与v、r无关)
带电粒子在有界磁场中运动的求解方法
1、定圆心
(1)已知入射方向和出射方向时,可以通过入射点和出射点作垂直于入射方向和出射方向的垂线,两条垂线的交点就是圆弧轨迹的圆心。
v
o
r
定圆心
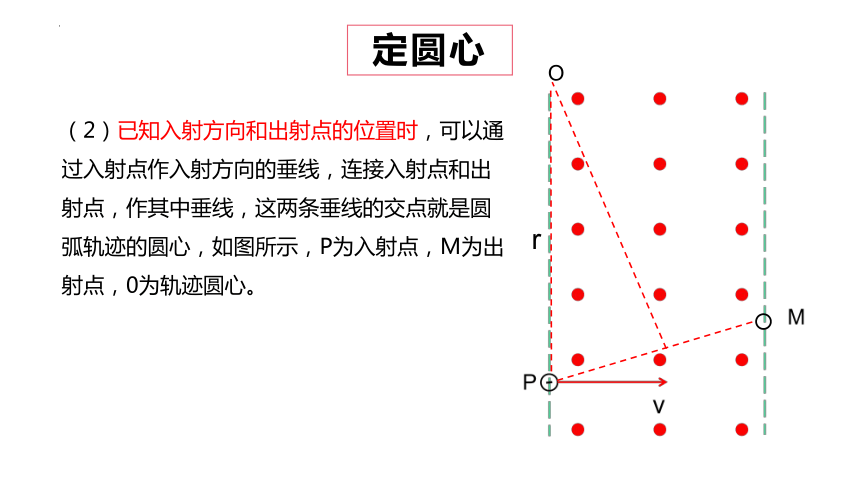
(2)已知入射方向和出射点的位置时,可以通过入射点作入射方向的垂线,连接入射点和出射点,作其中垂线,这两条垂线的交点就是圆弧轨迹的圆心,如图所示,P为入射点,M为出射点,0为轨迹圆心。
O
r
定圆心
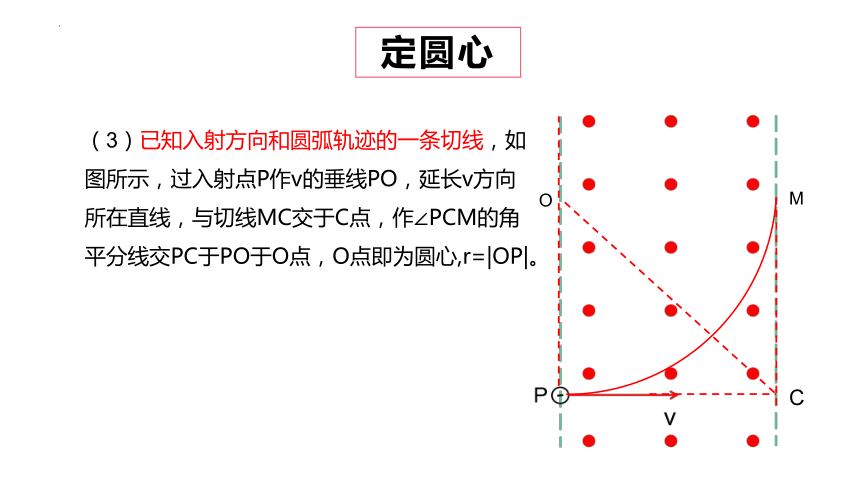
(3)已知入射方向和圆弧轨迹的一条切线,如图所示,过入射点P作v的垂线PO,延长v方向所在直线,与切线MC交于C点,作∠PCM的角平分线交PC于PO于O点,O点即为圆心,r=|OP|。
M
C
O
2、求半径
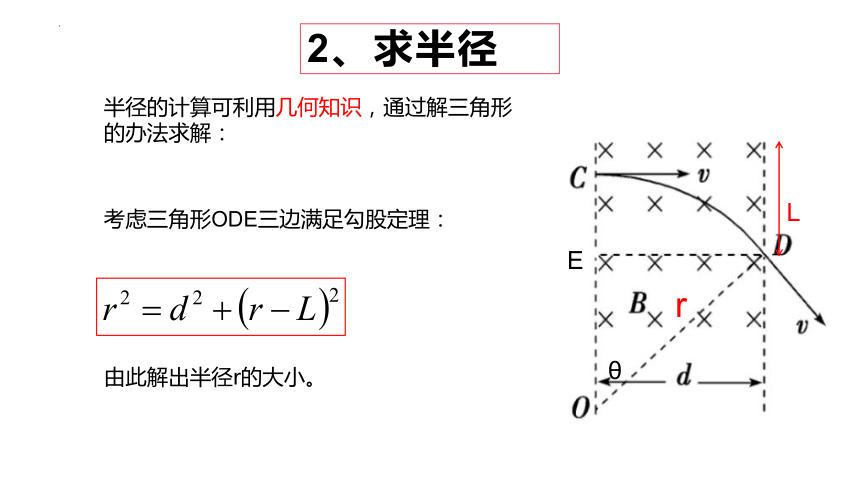
半径的计算可利用几何知识,通过解三角形的办法求解:
考虑三角形ODE三边满足勾股定理:
r
θ
L
E
由此解出半径r的大小。
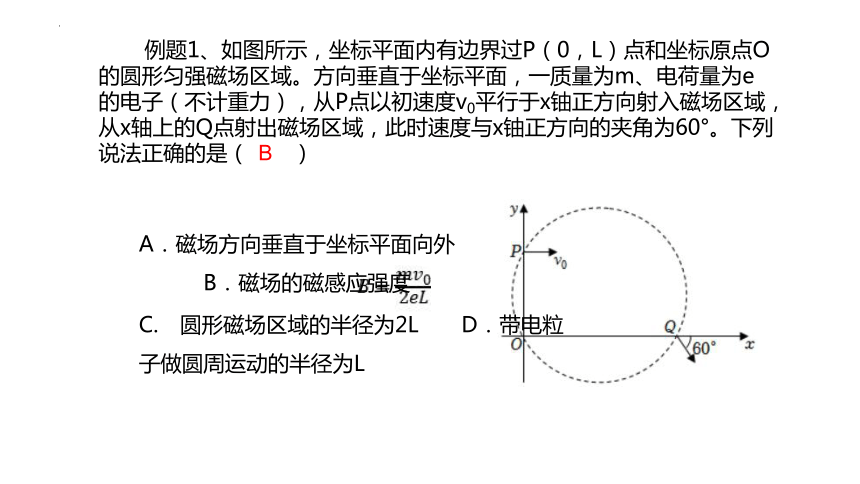
例题1、如图所示,坐标平面内有边界过P(0,L)点和坐标原点O的圆形匀强磁场区域。方向垂直于坐标平面,一质量为m、电荷量为e的电子(不计重力),从P点以初速度v0平行于x铀正方向射入磁场区域,从x轴上的Q点射出磁场区域,此时速度与x铀正方向的夹角为60°。下列说法正确的是( )
A.磁场方向垂直于坐标平面向外 B.磁场的磁感应强度
C. 圆形磁场区域的半径为2L D.带电粒子做圆周运动的半径为L
B
【解答】解:A、粒子运动的轨迹如图,根据左手定则可知磁场垂直纸面向里,故A错误;
BD、设粒子的轨迹半径为r(图中的O2P和O2Q),根据几何知识可知
解得粒子的轨道半径为r=2L,根据牛顿第二定律有:
联立解得:
故B正确,D错误;C、根据几何知识可知,由于∠QOP=90°,故PQ为圆形磁场区域的直径,故2R=r,则磁场区域的半径R=L,故C错误;故选:B。
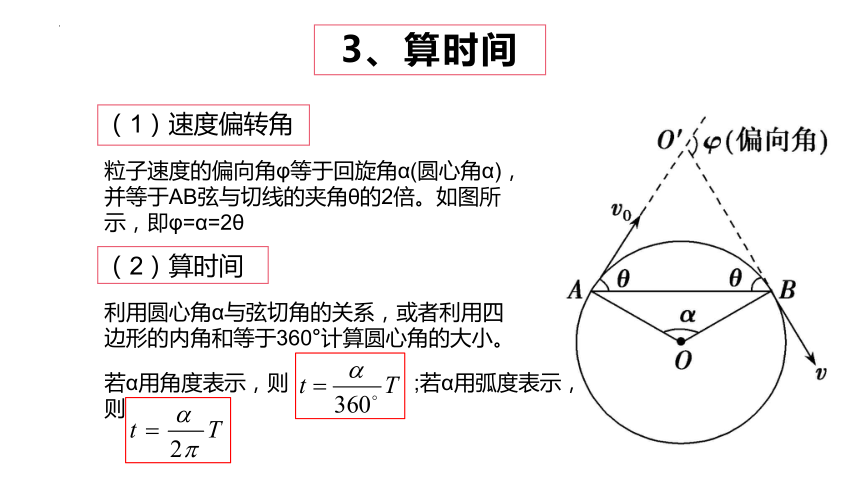
3、算时间
(1)速度偏转角
粒子速度的偏向角φ等于回旋角α(圆心角α),并等于AB弦与切线的夹角θ的2倍。如图所示,即φ=α=2θ
(2)算时间
利用圆心角α与弦切角的关系,或者利用四边形的内角和等于360°计算圆心角的大小。
若α用角度表示,则 ;若α用弧度表示,则
例题2、如图所示为一圆形区域的匀强磁场,在O点处有一放射源,沿半径方向射出速度为v的不同带电拉子,其中带电粒子1从A点飞出磁场,带电粒子2从B点飞出磁场,不考虑带电粒子的重力,则( )
A.带电粒子1与带电粒子2在磁场中运动时间的比2:3 B.带电粒子1与带电粒子2做圆周运动的半径比为
C.带电粒子1的比荷与带电粒子2的比荷的比为1:3 D.带电粒子1与带电粒子2在磁场中周期比为3:1
A
【解答】解:B、设磁场区域半径为R,粒子运动轨迹如图所示:
由几何知识得,粒子转过的圆心角:θ1=120°,θ2=60°,粒子的运动轨道半径:r1=Rtan30°,r2=Rtan60°,带电粒子1与带电粒子2做圆周运动的半径比r1:r2=1:3,故B错误;
C、洛伦兹力提供向心力,由牛顿第二定律得:
,带电粒子1的比荷与带电粒子2的比荷的比:
故C错误;
,带电粒子1与带电粒子2在磁场中周期比
,故D错误;A、粒子在磁场中的运动时间:
,带电粒子1与带电粒子2在磁场中运动时间的比
,故A正确。故选:A。
解得:
D、粒子在磁场中做圆周运动的周期:
直线边界
从某一直线边界射入的粒子,再从这一边界射出时,速度与边界的夹角相等,如图所示。
(多选)例题3、A、B两个带电粒子同时从匀强磁场的直线边界上的M、N点分别以45°和30°(与边界的夹角)射入磁场,又同时分别从N、M点穿出,如图所示。设边界上方的磁场范围足够大,下列说法中正确的是( )
A.A粒子带负电,B粒子带正电 B.A、B两粒子运动半径之比为1:
C.A、B两粒子速率之比为1:
D.A、B两粒子的比荷之比为3:2
BD
平行边界
带电粒子在平行边界的匀强磁场中运动,轨迹如图所示。这种情境经常出现带电粒子恰好从磁场飞出(或恰好飞不出)的临界问题。要寻找相关物理量的临界条件,总是先从轨迹入手,临界轨迹有两种情况:
轨迹与磁场边界端点相交,如图a
轨迹与磁场边界相切,如图c
例题4、如图所示,一束电子(电子电荷量为e)以与上边界夹角为60°的速度v由A点射入磁感应强度为B、宽度为d的平行边界的匀强磁场中,在C点穿出磁场时的速度方向与磁场下边界垂直。则电子的质量是多少?电子穿过磁场的时间是多少?
【解答】解:电子在磁场中做匀速圆周运动,垂直射出匀强磁场,运动轨迹如图所示:
由几何知识得:θ=30°,d=Rsin30°,由牛顿第二定律得:
解得:
由几何知识得到,轨迹的圆心角为:θ=30°,电子在磁场中的周期
电子在磁场中的运动时间为:
解得:
矩形磁场
带电粒子垂直于矩形磁场的边界入射的情况,如图所示。
轨迹半径
运动时间
r
θ
L
E
偏转角的正弦值
例题5、如图所示、长为L、宽为 的矩形区域abcd内有匀强磁场,匀强磁场的磁感应强度大小为B,方向垂直纸面向外。一质量为m、电荷量为+q的带电粒子沿着矩形磁场的上边界从左侧射入磁场,粒子的重力不计。(1)若带电粒子垂直下边界cd射出磁场,求带电粒子的速率。(2)若带电粒子从右边界bc射出磁场,求带电粒子的速率v的取值范围。
【解答】解:(1)粒子运动轨迹如图1所示
由几何知识可知,粒子做匀速圆周运动的轨道半径:
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
解得:
(2)粒子运动轨迹通过c点时粒子恰好从bc边射出磁场,粒子运动轨迹如图2所示
由几何知识得:
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
解得:
,粒子从右边界bc射出磁场,粒子的速率
解得
圆形磁场
在圆形磁场区域内,沿半径方向射入的粒子,必沿半径方向射出,如图所示。
例题6、如图,一半径为R的圆表示一柱形区域的横截面(纸面),O为圆心.在柱形区域内加一方向垂直于纸面向外的匀强磁场,一质量为m、电荷量为+q的粒子沿图中直径从圆上的A点射入柱形区域,在圆上的D点离开该区域,已知图中θ=120°,现将磁场换为竖直向下的匀强电场,同一粒子以同样速度沿直径从A点射入柱形区域,也在D点离开该区域.若磁感应强度大小为B,不计重力,试求:(1)带电粒子做匀速圆周运动的半径r;(2)电场强度E的大小.
【解答】解:(1)画出粒子轨迹图,如图所示,
由几何关系得:
(2)粒子在磁场中做圆周运动.设圆周的半径为r,由牛顿第二定律和洛伦兹力公式得:
加电场时,粒子做类平抛运动,根据类平抛规律可得:R(1+cos60°)=vt
由牛顿第二定律:Eq=ma
解得:
1、带电粒子在匀强磁场中的运动
当带电粒子速度与磁场方向垂直时:
匀速圆周运动
洛伦兹力提供向心力
圆周运动的半径
2、带电粒子在匀强磁场中做匀速圆周运动的规律
圆周运动的周期
课堂小结
3、定圆心、求半径、求时间
4、不同类型的磁场边界
1.2带电粒子在有界磁场中的运动
回顾:做匀速圆周运动的半径和周期
(1)轨道半径
做由于洛伦兹力提供向心力,则有 ,得到轨道半径为 ,粒子的轨道半径与粒子的速率成正比。
(2)周期
由轨道半径与周期之间的关系知 (与v、r无关)
带电粒子在有界磁场中运动的求解方法
1、定圆心
(1)已知入射方向和出射方向时,可以通过入射点和出射点作垂直于入射方向和出射方向的垂线,两条垂线的交点就是圆弧轨迹的圆心。
v
o
r
定圆心
(2)已知入射方向和出射点的位置时,可以通过入射点作入射方向的垂线,连接入射点和出射点,作其中垂线,这两条垂线的交点就是圆弧轨迹的圆心,如图所示,P为入射点,M为出射点,0为轨迹圆心。
O
r
定圆心
(3)已知入射方向和圆弧轨迹的一条切线,如图所示,过入射点P作v的垂线PO,延长v方向所在直线,与切线MC交于C点,作∠PCM的角平分线交PC于PO于O点,O点即为圆心,r=|OP|。
M
C
O
2、求半径
半径的计算可利用几何知识,通过解三角形的办法求解:
考虑三角形ODE三边满足勾股定理:
r
θ
L
E
由此解出半径r的大小。
例题1、如图所示,坐标平面内有边界过P(0,L)点和坐标原点O的圆形匀强磁场区域。方向垂直于坐标平面,一质量为m、电荷量为e的电子(不计重力),从P点以初速度v0平行于x铀正方向射入磁场区域,从x轴上的Q点射出磁场区域,此时速度与x铀正方向的夹角为60°。下列说法正确的是( )
A.磁场方向垂直于坐标平面向外 B.磁场的磁感应强度
C. 圆形磁场区域的半径为2L D.带电粒子做圆周运动的半径为L
B
【解答】解:A、粒子运动的轨迹如图,根据左手定则可知磁场垂直纸面向里,故A错误;
BD、设粒子的轨迹半径为r(图中的O2P和O2Q),根据几何知识可知
解得粒子的轨道半径为r=2L,根据牛顿第二定律有:
联立解得:
故B正确,D错误;C、根据几何知识可知,由于∠QOP=90°,故PQ为圆形磁场区域的直径,故2R=r,则磁场区域的半径R=L,故C错误;故选:B。
3、算时间
(1)速度偏转角
粒子速度的偏向角φ等于回旋角α(圆心角α),并等于AB弦与切线的夹角θ的2倍。如图所示,即φ=α=2θ
(2)算时间
利用圆心角α与弦切角的关系,或者利用四边形的内角和等于360°计算圆心角的大小。
若α用角度表示,则 ;若α用弧度表示,则
例题2、如图所示为一圆形区域的匀强磁场,在O点处有一放射源,沿半径方向射出速度为v的不同带电拉子,其中带电粒子1从A点飞出磁场,带电粒子2从B点飞出磁场,不考虑带电粒子的重力,则( )
A.带电粒子1与带电粒子2在磁场中运动时间的比2:3 B.带电粒子1与带电粒子2做圆周运动的半径比为
C.带电粒子1的比荷与带电粒子2的比荷的比为1:3 D.带电粒子1与带电粒子2在磁场中周期比为3:1
A
【解答】解:B、设磁场区域半径为R,粒子运动轨迹如图所示:
由几何知识得,粒子转过的圆心角:θ1=120°,θ2=60°,粒子的运动轨道半径:r1=Rtan30°,r2=Rtan60°,带电粒子1与带电粒子2做圆周运动的半径比r1:r2=1:3,故B错误;
C、洛伦兹力提供向心力,由牛顿第二定律得:
,带电粒子1的比荷与带电粒子2的比荷的比:
故C错误;
,带电粒子1与带电粒子2在磁场中周期比
,故D错误;A、粒子在磁场中的运动时间:
,带电粒子1与带电粒子2在磁场中运动时间的比
,故A正确。故选:A。
解得:
D、粒子在磁场中做圆周运动的周期:
直线边界
从某一直线边界射入的粒子,再从这一边界射出时,速度与边界的夹角相等,如图所示。
(多选)例题3、A、B两个带电粒子同时从匀强磁场的直线边界上的M、N点分别以45°和30°(与边界的夹角)射入磁场,又同时分别从N、M点穿出,如图所示。设边界上方的磁场范围足够大,下列说法中正确的是( )
A.A粒子带负电,B粒子带正电 B.A、B两粒子运动半径之比为1:
C.A、B两粒子速率之比为1:
D.A、B两粒子的比荷之比为3:2
BD
平行边界
带电粒子在平行边界的匀强磁场中运动,轨迹如图所示。这种情境经常出现带电粒子恰好从磁场飞出(或恰好飞不出)的临界问题。要寻找相关物理量的临界条件,总是先从轨迹入手,临界轨迹有两种情况:
轨迹与磁场边界端点相交,如图a
轨迹与磁场边界相切,如图c
例题4、如图所示,一束电子(电子电荷量为e)以与上边界夹角为60°的速度v由A点射入磁感应强度为B、宽度为d的平行边界的匀强磁场中,在C点穿出磁场时的速度方向与磁场下边界垂直。则电子的质量是多少?电子穿过磁场的时间是多少?
【解答】解:电子在磁场中做匀速圆周运动,垂直射出匀强磁场,运动轨迹如图所示:
由几何知识得:θ=30°,d=Rsin30°,由牛顿第二定律得:
解得:
由几何知识得到,轨迹的圆心角为:θ=30°,电子在磁场中的周期
电子在磁场中的运动时间为:
解得:
矩形磁场
带电粒子垂直于矩形磁场的边界入射的情况,如图所示。
轨迹半径
运动时间
r
θ
L
E
偏转角的正弦值
例题5、如图所示、长为L、宽为 的矩形区域abcd内有匀强磁场,匀强磁场的磁感应强度大小为B,方向垂直纸面向外。一质量为m、电荷量为+q的带电粒子沿着矩形磁场的上边界从左侧射入磁场,粒子的重力不计。(1)若带电粒子垂直下边界cd射出磁场,求带电粒子的速率。(2)若带电粒子从右边界bc射出磁场,求带电粒子的速率v的取值范围。
【解答】解:(1)粒子运动轨迹如图1所示
由几何知识可知,粒子做匀速圆周运动的轨道半径:
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
解得:
(2)粒子运动轨迹通过c点时粒子恰好从bc边射出磁场,粒子运动轨迹如图2所示
由几何知识得:
粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:
解得:
,粒子从右边界bc射出磁场,粒子的速率
解得
圆形磁场
在圆形磁场区域内,沿半径方向射入的粒子,必沿半径方向射出,如图所示。
例题6、如图,一半径为R的圆表示一柱形区域的横截面(纸面),O为圆心.在柱形区域内加一方向垂直于纸面向外的匀强磁场,一质量为m、电荷量为+q的粒子沿图中直径从圆上的A点射入柱形区域,在圆上的D点离开该区域,已知图中θ=120°,现将磁场换为竖直向下的匀强电场,同一粒子以同样速度沿直径从A点射入柱形区域,也在D点离开该区域.若磁感应强度大小为B,不计重力,试求:(1)带电粒子做匀速圆周运动的半径r;(2)电场强度E的大小.
【解答】解:(1)画出粒子轨迹图,如图所示,
由几何关系得:
(2)粒子在磁场中做圆周运动.设圆周的半径为r,由牛顿第二定律和洛伦兹力公式得:
加电场时,粒子做类平抛运动,根据类平抛规律可得:R(1+cos60°)=vt
由牛顿第二定律:Eq=ma
解得:
1、带电粒子在匀强磁场中的运动
当带电粒子速度与磁场方向垂直时:
匀速圆周运动
洛伦兹力提供向心力
圆周运动的半径
2、带电粒子在匀强磁场中做匀速圆周运动的规律
圆周运动的周期
课堂小结
3、定圆心、求半径、求时间
4、不同类型的磁场边界
