河南省七大名校巅峰计划2022-2023学年高一下学期期末考试物理试题(无答案)
文档属性
| 名称 | 河南省七大名校巅峰计划2022-2023学年高一下学期期末考试物理试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 196.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-07-19 00:27:25 | ||
图片预览



文档简介
河南省七大名校巅峰计划2022-2023学年高一下学期期末考试
物 理
本试卷满分100分,考试时间75分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上, 并将自己的姓名、准考证号、座位号填写在本试卷上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑; 如需改动,用橡皮擦干净后,再选涂其他答案标号。涂写在本试卷上无效。
3.作答非选择题时,将答案书写在答题卡上,书写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
一、单选题: 共7小题, 每题 4分,共28分。
1.一根质量均匀的细杆斜靠在墙上,地面光滑。初始时杆与墙面夹角为60°,在杆滑下的过程中,墙对杆的作用力
A.先增大后减小至0 B.先增大后减小,但不会减为0
C.一直增大 D.一直减小
2.2023年7月14日,美国的 LIGO探测设施接收到一个来自 GW150914的引力波信号,此信号是由两个黑洞的合并过程产生的。如果将某个双黑洞系统简化为如图所示的圆周运动模型,两黑洞绕O点做匀速圆周运动。在相互强大的引力作用下,两黑洞间的距离逐渐减小,在此过程中,两黑洞做圆周运动的
A.向心力均逐渐减小 B.线速度均逐渐减小
C.周期均不变 D.角速度均逐渐增大
3.某同学在高度 h处以一定大小的速度 v0抛出一小球,当其速度方向不同时,落地点与抛出点的水平距离即射程大小也不同,若不计空气阻力,则最大射程为
A. B. C. D.
4.如图所示,滑块A 和足够长的木板 B叠放在水平地面上,A 和 B之间的动摩擦因数是 B和地面之间的动摩擦因数的4倍,A和B的质量均为m。现对A施加一水平向右逐渐增大的力 F, 当F增大到 F0时A开始运动,之后力 F按图乙所示的规律继续增大,图乙中的x为A运动的位移,已知最大静摩擦力等于滑动摩擦力。对两物块的运动过程, 以下说法正确的是
A.当F>2F0,木块A 和木板 B开始相对滑动
B.当F>F0,木块A 和木板B开始相对滑动
C. 自x=0至木板x=x0木板 B对 A做功大小为
D. x=x0时,木板B的速度大小为
5.由n个带电量均为Q的可视为质点的带电小球无间隙排列构成的半径为 R的圆环固定在竖直平面内。一个质量为m的金属小球(视为质点)通过长为 L=2R的绝缘细线悬挂在圆环的最高点。当金属小球电荷量也为Q(未知)时,发现金属小球在垂直圆环平面的对称轴上 P点处于平衡状态,如图所示,轴线上的两点 P、P'关于圆心O对称。已知静电力常量为 k,重力加速度为g,取无穷远处电势为零。则下列说法中正确的是
A. O点的场强一定为零
B.由于 P、P'两点关于 O点对称,两点的场强大小相等,方向相反
C.金属带电小球的电量为
D.固定 P处的小球,然后在圆环上取下一个小球(其余 n-1个小球位置不变)置于 P'处,则圆心 O的场强大小为
6.如图所示,一辆卡车在水平路面上行驶。初速度为 54km/h。其车厢长度为 10.0m,在车尾边缘处放有一个货箱, 其长宽高皆为0.5m。卡车加速时的最大加速度为 2.2m/s2,卡车刹车时的最大加速度为 3m/s2。已知货箱和车厢之间的动摩擦因数为 0.24(最大静摩擦因数约等于动摩擦因数,g=10m/s2),则下列说法正确的是
A.若司机全力加速, 货箱有可能掉出车厢
B.若司机全力刹车,货箱不可能碰到车头
C.若司机全力刹车,货箱碰到车头的时间介于刹车后 5s到 6s之间
D.若司机全力刹车,货箱碰到车头的时间介于刹车后 6s到7s之间
7.某人驾驶一辆汽车甲正在平直的公路上以某一速度匀速运动,突然发现前方 50m处停着一辆乙车,立即刹车,刹车后做匀减速直线运动。已知刹车后第1个2s内的位移是24m,第4个2s内的位移是 1m。则下列说法中正确的是
A.汽车甲刹车后做匀减速直线运动的加速度大小为 2m/s2
B.汽车甲刹车后做匀减速直线运动的加速度大小为
C.汽车甲刹车后停止前,可能撞上乙车
D.汽车甲刹车前的速度为 13.9m/s
二、多选题: 共3小题, 每小题6分,共18分。每小题给出的四个选项中有多个选项正确,全部选对的得6分,选对但不全的得3分,有错选的得0分。
8.如图所示, 圆柱形管的底端固定一弹射器,弹射器上有一质量m1=1kg的小滑块,管和弹射器的总质量m2=2kg,滑块与管内壁间的滑动摩擦力大小为 0.4m1g。整个装置竖直静止在水平地面上。发射时,滑块离开弹射器瞬间距离上管口的距离为1.0m;滑块离开弹射器后能上升的最大高度为 1.4m,小滑块可视为质点且弹射时间极短, 每次弹射后滑块获得的初速度相等,忽略空气阻力,取重力加速度g=10m/s2。则下列说法正确的是
A.滑块从离开弹射器到第二次通过圆柱形管上端经历的时间为
B.滑块从离开弹射器到再次回到弹射器处经历的时间为
C.当滑块离开弹射器瞬间,对圆柱形管施加一个竖直向上的恒力 F, 为保证滑块不滑出管口, F的最小值为 24N
D.当滑块离开弹射器瞬间,对圆柱形管施加一个竖直向上的恒力 F, 为保证滑块不滑出管口,F的最小值为 20N
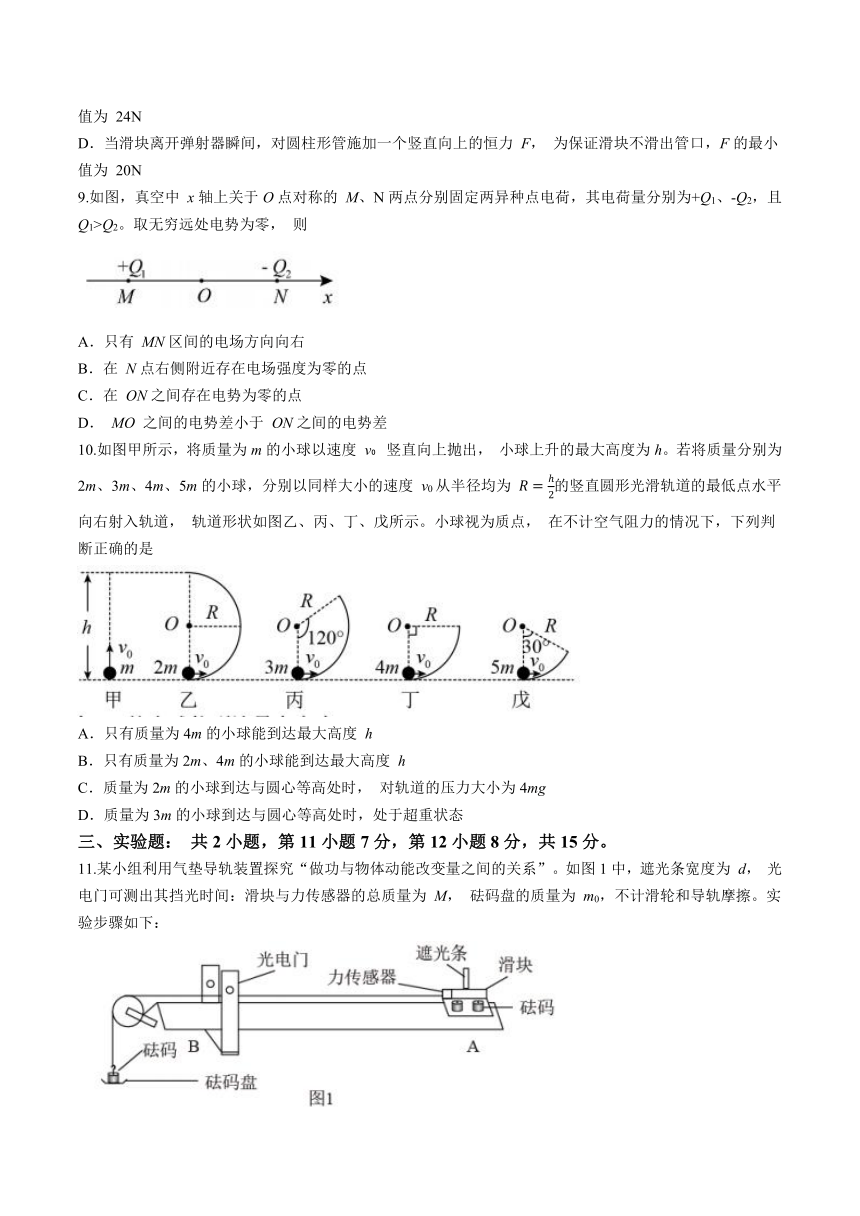
9.如图,真空中 x轴上关于O点对称的 M、N两点分别固定两异种点电荷,其电荷量分别为+Q1、-Q2,且Q1>Q2。取无穷远处电势为零, 则
A.只有 MN区间的电场方向向右
B.在 N点右侧附近存在电场强度为零的点
C.在 ON之间存在电势为零的点
D. MO 之间的电势差小于 ON之间的电势差
10.如图甲所示,将质量为m的小球以速度 v 竖直向上抛出, 小球上升的最大高度为h。若将质量分别为2m、3m、4m、5m的小球,分别以同样大小的速度 v0从半径均为 的竖直圆形光滑轨道的最低点水平向右射入轨道, 轨道形状如图乙、丙、丁、戊所示。小球视为质点, 在不计空气阻力的情况下,下列判断正确的是
A.只有质量为4m的小球能到达最大高度 h
B.只有质量为2m、4m的小球能到达最大高度 h
C.质量为2m的小球到达与圆心等高处时, 对轨道的压力大小为4mg
D.质量为3m的小球到达与圆心等高处时,处于超重状态
三、实验题: 共2小题,第11小题7分,第12小题8分,共15分。
11.某小组利用气垫导轨装置探究“做功与物体动能改变量之间的关系”。如图1中,遮光条宽度为 d, 光电门可测出其挡光时间:滑块与力传感器的总质量为 M, 砝码盘的质量为 m0,不计滑轮和导轨摩擦。实验步骤如下:
①调节气垫导轨使其水平,并取5个质量均为 m的砝码放在滑块上:
②用细绳连接砝码盘与力传感器和滑块,让滑块静止放在导轨右侧的某一位置, 测出遮光条到光电门的距离为 S;
③从滑块上取出一个砝码放在砝码盘中,释放滑块后,记录此时力传感器的值为 F,测出遮光条经过光电门的挡光时间 Δt;
④再从滑块上取出一个砝码放在砝码盘中,重复步骤③, 并保证滑块从同一个位置静止释放;
⑤重复步骤④,直至滑块上的砝码全部放入到砝码盘中。
请完成下面问题:
(1)若用十分度的游标卡尺测得遮光条宽度d如图3, 则 d= mm;
(2)滑块经过光电门时的速度可用 v= (用题中所给的字母表示,下同)计算;
(3)在处理步骤③所记录的实验数据时,甲同学理解的合外力做功为 W =FS, 则其对应动能变化量应当是 = ;
(4)乙同学按照甲同学的思路,根据实验数据得到 的图线如图4所示,则其斜率k= 。
12.用如图所示的实验装置来验证向心力公式。匀质小球由轻绳a和b分别系于一轻质木架上的A点和C点。当木架绕轴BC匀速转动时,小球在水平面内做匀速圆周运动,绳 a 在竖直方向、绳在水平方向。两绳的 A、C端分别安装有拉力传感器1、2,重力加速度为 g,忽略空气的阻力,实验步骤如下:
A.实验之前,用游标卡尺测得小球的直径为 d,用刻度尺测得 a绳的长度为 la, b绳的长度为 lb;
B.使木架绕BC轴匀速转动,并带动小球在水平面内做匀速圆周运动,记录转 n圈对应的时间 t;
C.读出拉力传感器1、2的示数分别为 Fa、Fb;
D.当小球运动到图示位置时, 绳b被突然烧断,同时木架也立即停止转动,读出拉力传感器1在此瞬间的示数为 F0。
(1)小球的质量 m= ,做匀速圆周运动的周期 T= ;
(2)绳b被烧断之前小球做匀速圆周运动,若等式 成立,则向心力公式得到验证; (用Fa、Fb、n、t、g、lb和d表示)
(3)绳b被烧断之后的瞬间,若等式 成立,则向心力公式得到验证。(用F0、Fa、n、t、g、lb和d表示)
四、解答题: 共3小题, 第 13小题10分,第14小题11分,第15 小题18分,共39分。
13.一端弯曲的光滑绝缘轨道 ABN固定在竖直平面上,如图所示, AB段水平、BN段是半径为 R的半圆弧,有一个正点电荷固定在圆心O处。一质量为 m带正电小环,在水平恒力 作用下从C点由静止开始运动,到B点时撤去外力,小环继续运动,发现刚好能到达绝缘轨道上与圆心等高的 M点,已知 CB间距为 已知小环在圆轨道上时受到圆心处的点电荷的静电力大小为 2mg。求:
(1)小环从C运动到 M过程中,点电荷Q的电场力对它做的功;
(2)若水平恒力大小改为2F,则小环在能达到的最高点 N时的速度大小;
(3)小环在距离 B点 的D点以向右的初速度 运动,在静电力的作用下运动到 B点的速度恰好为0。若在 D点施加最小的恒定外力作用由静止开始运动,则小环在圆轨道上能到达的最大高度值多少?
14.如图所示, 足够长的斜面与水平面夹角为 37°,斜面上有一质量 M=3kg的长木板,斜面底端挡板高度与木板厚度相同。 m=1kg的小物块从空中某点以 v0=3m/s水平抛出,抛出同时木板由静止释放,小物块下降 h=0.8m 掉在木板前端,碰撞时间极短,可忽略不计,碰后瞬间物块垂直斜面的分速度立即变为零。碰后两者向下运动,小物块恰好在木板与挡板碰撞时在挡板处离开木板。已知木板与斜面间动摩擦因数 μ=0.5,木板上表面光滑,木板与挡板每次碰撞均无能量损失,g=10m/s2,求:
(1)碰前瞬间小物块速度大小和方向;
(2)木板至少多长小物块才没有从木板后端离开木板?
(3)木板从开始运动到最后停在斜面底端的整个过程中通过路程多大?
15.牛顿在前人研究的基础上,利用他的运动定律把行星的向心加速度与太阳对它的引力联系起来,巧妙推导出太阳和行星之间的引力关系。
(1)行星围绕太阳的运动当做匀速圆周运动,已知行星的质量为 m,太阳的质量为 M,行星与太阳中心之间的距离为 r,请利用牛顿定律和开普勒定律导出太阳和行星之间的引力表达式
(2)牛顿思考月球绕地球运行的原因时,苹果偶然落地引起了他的遐想: 拉住月球使它围绕地球运动的力与拉着苹果下落的力,是否都与太阳吸引行星的力性质相同,遵循着统一的规律:平方反比规律?因此,牛顿开始了著名的“月—地检验”。
a.已知月球与地球的距离约为地球半径的60倍,如果牛顿的猜想正确,请你据此计算月球公转的向心加速度 a和苹果下落的加速度g的比值
b.在牛顿的时代,月球与地球的距离r′、月球绕地球公转的周期T′等都能比较精确地测定,请你据此写出计算月球公转的向心加速度 a 的表达式; 已知r'≈3.84×108m, T≈2.36×106s,地面附近的重力加速度g=9.80m/s2,请你根据这些数据估算比值 a; 与(1)中的结果相比较,你能得出什么结论?
c.假如有一颗在赤道上的苹果树,长到了月亮的高度。请你根据苹果的运动状态进行受力分析,在图中的树枝上画出一个长势符合物理规律的苹果,并推断如果树冠上的苹果被人用剪刀剪离树枝,苹果是否会落回地面?(分析过程中可忽略其它星球对苹果的作用)。
物 理
本试卷满分100分,考试时间75分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上, 并将自己的姓名、准考证号、座位号填写在本试卷上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑; 如需改动,用橡皮擦干净后,再选涂其他答案标号。涂写在本试卷上无效。
3.作答非选择题时,将答案书写在答题卡上,书写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
一、单选题: 共7小题, 每题 4分,共28分。
1.一根质量均匀的细杆斜靠在墙上,地面光滑。初始时杆与墙面夹角为60°,在杆滑下的过程中,墙对杆的作用力
A.先增大后减小至0 B.先增大后减小,但不会减为0
C.一直增大 D.一直减小
2.2023年7月14日,美国的 LIGO探测设施接收到一个来自 GW150914的引力波信号,此信号是由两个黑洞的合并过程产生的。如果将某个双黑洞系统简化为如图所示的圆周运动模型,两黑洞绕O点做匀速圆周运动。在相互强大的引力作用下,两黑洞间的距离逐渐减小,在此过程中,两黑洞做圆周运动的
A.向心力均逐渐减小 B.线速度均逐渐减小
C.周期均不变 D.角速度均逐渐增大
3.某同学在高度 h处以一定大小的速度 v0抛出一小球,当其速度方向不同时,落地点与抛出点的水平距离即射程大小也不同,若不计空气阻力,则最大射程为
A. B. C. D.
4.如图所示,滑块A 和足够长的木板 B叠放在水平地面上,A 和 B之间的动摩擦因数是 B和地面之间的动摩擦因数的4倍,A和B的质量均为m。现对A施加一水平向右逐渐增大的力 F, 当F增大到 F0时A开始运动,之后力 F按图乙所示的规律继续增大,图乙中的x为A运动的位移,已知最大静摩擦力等于滑动摩擦力。对两物块的运动过程, 以下说法正确的是
A.当F>2F0,木块A 和木板 B开始相对滑动
B.当F>F0,木块A 和木板B开始相对滑动
C. 自x=0至木板x=x0木板 B对 A做功大小为
D. x=x0时,木板B的速度大小为
5.由n个带电量均为Q的可视为质点的带电小球无间隙排列构成的半径为 R的圆环固定在竖直平面内。一个质量为m的金属小球(视为质点)通过长为 L=2R的绝缘细线悬挂在圆环的最高点。当金属小球电荷量也为Q(未知)时,发现金属小球在垂直圆环平面的对称轴上 P点处于平衡状态,如图所示,轴线上的两点 P、P'关于圆心O对称。已知静电力常量为 k,重力加速度为g,取无穷远处电势为零。则下列说法中正确的是
A. O点的场强一定为零
B.由于 P、P'两点关于 O点对称,两点的场强大小相等,方向相反
C.金属带电小球的电量为
D.固定 P处的小球,然后在圆环上取下一个小球(其余 n-1个小球位置不变)置于 P'处,则圆心 O的场强大小为
6.如图所示,一辆卡车在水平路面上行驶。初速度为 54km/h。其车厢长度为 10.0m,在车尾边缘处放有一个货箱, 其长宽高皆为0.5m。卡车加速时的最大加速度为 2.2m/s2,卡车刹车时的最大加速度为 3m/s2。已知货箱和车厢之间的动摩擦因数为 0.24(最大静摩擦因数约等于动摩擦因数,g=10m/s2),则下列说法正确的是
A.若司机全力加速, 货箱有可能掉出车厢
B.若司机全力刹车,货箱不可能碰到车头
C.若司机全力刹车,货箱碰到车头的时间介于刹车后 5s到 6s之间
D.若司机全力刹车,货箱碰到车头的时间介于刹车后 6s到7s之间
7.某人驾驶一辆汽车甲正在平直的公路上以某一速度匀速运动,突然发现前方 50m处停着一辆乙车,立即刹车,刹车后做匀减速直线运动。已知刹车后第1个2s内的位移是24m,第4个2s内的位移是 1m。则下列说法中正确的是
A.汽车甲刹车后做匀减速直线运动的加速度大小为 2m/s2
B.汽车甲刹车后做匀减速直线运动的加速度大小为
C.汽车甲刹车后停止前,可能撞上乙车
D.汽车甲刹车前的速度为 13.9m/s
二、多选题: 共3小题, 每小题6分,共18分。每小题给出的四个选项中有多个选项正确,全部选对的得6分,选对但不全的得3分,有错选的得0分。
8.如图所示, 圆柱形管的底端固定一弹射器,弹射器上有一质量m1=1kg的小滑块,管和弹射器的总质量m2=2kg,滑块与管内壁间的滑动摩擦力大小为 0.4m1g。整个装置竖直静止在水平地面上。发射时,滑块离开弹射器瞬间距离上管口的距离为1.0m;滑块离开弹射器后能上升的最大高度为 1.4m,小滑块可视为质点且弹射时间极短, 每次弹射后滑块获得的初速度相等,忽略空气阻力,取重力加速度g=10m/s2。则下列说法正确的是
A.滑块从离开弹射器到第二次通过圆柱形管上端经历的时间为
B.滑块从离开弹射器到再次回到弹射器处经历的时间为
C.当滑块离开弹射器瞬间,对圆柱形管施加一个竖直向上的恒力 F, 为保证滑块不滑出管口, F的最小值为 24N
D.当滑块离开弹射器瞬间,对圆柱形管施加一个竖直向上的恒力 F, 为保证滑块不滑出管口,F的最小值为 20N
9.如图,真空中 x轴上关于O点对称的 M、N两点分别固定两异种点电荷,其电荷量分别为+Q1、-Q2,且Q1>Q2。取无穷远处电势为零, 则
A.只有 MN区间的电场方向向右
B.在 N点右侧附近存在电场强度为零的点
C.在 ON之间存在电势为零的点
D. MO 之间的电势差小于 ON之间的电势差
10.如图甲所示,将质量为m的小球以速度 v 竖直向上抛出, 小球上升的最大高度为h。若将质量分别为2m、3m、4m、5m的小球,分别以同样大小的速度 v0从半径均为 的竖直圆形光滑轨道的最低点水平向右射入轨道, 轨道形状如图乙、丙、丁、戊所示。小球视为质点, 在不计空气阻力的情况下,下列判断正确的是
A.只有质量为4m的小球能到达最大高度 h
B.只有质量为2m、4m的小球能到达最大高度 h
C.质量为2m的小球到达与圆心等高处时, 对轨道的压力大小为4mg
D.质量为3m的小球到达与圆心等高处时,处于超重状态
三、实验题: 共2小题,第11小题7分,第12小题8分,共15分。
11.某小组利用气垫导轨装置探究“做功与物体动能改变量之间的关系”。如图1中,遮光条宽度为 d, 光电门可测出其挡光时间:滑块与力传感器的总质量为 M, 砝码盘的质量为 m0,不计滑轮和导轨摩擦。实验步骤如下:
①调节气垫导轨使其水平,并取5个质量均为 m的砝码放在滑块上:
②用细绳连接砝码盘与力传感器和滑块,让滑块静止放在导轨右侧的某一位置, 测出遮光条到光电门的距离为 S;
③从滑块上取出一个砝码放在砝码盘中,释放滑块后,记录此时力传感器的值为 F,测出遮光条经过光电门的挡光时间 Δt;
④再从滑块上取出一个砝码放在砝码盘中,重复步骤③, 并保证滑块从同一个位置静止释放;
⑤重复步骤④,直至滑块上的砝码全部放入到砝码盘中。
请完成下面问题:
(1)若用十分度的游标卡尺测得遮光条宽度d如图3, 则 d= mm;
(2)滑块经过光电门时的速度可用 v= (用题中所给的字母表示,下同)计算;
(3)在处理步骤③所记录的实验数据时,甲同学理解的合外力做功为 W =FS, 则其对应动能变化量应当是 = ;
(4)乙同学按照甲同学的思路,根据实验数据得到 的图线如图4所示,则其斜率k= 。
12.用如图所示的实验装置来验证向心力公式。匀质小球由轻绳a和b分别系于一轻质木架上的A点和C点。当木架绕轴BC匀速转动时,小球在水平面内做匀速圆周运动,绳 a 在竖直方向、绳在水平方向。两绳的 A、C端分别安装有拉力传感器1、2,重力加速度为 g,忽略空气的阻力,实验步骤如下:
A.实验之前,用游标卡尺测得小球的直径为 d,用刻度尺测得 a绳的长度为 la, b绳的长度为 lb;
B.使木架绕BC轴匀速转动,并带动小球在水平面内做匀速圆周运动,记录转 n圈对应的时间 t;
C.读出拉力传感器1、2的示数分别为 Fa、Fb;
D.当小球运动到图示位置时, 绳b被突然烧断,同时木架也立即停止转动,读出拉力传感器1在此瞬间的示数为 F0。
(1)小球的质量 m= ,做匀速圆周运动的周期 T= ;
(2)绳b被烧断之前小球做匀速圆周运动,若等式 成立,则向心力公式得到验证; (用Fa、Fb、n、t、g、lb和d表示)
(3)绳b被烧断之后的瞬间,若等式 成立,则向心力公式得到验证。(用F0、Fa、n、t、g、lb和d表示)
四、解答题: 共3小题, 第 13小题10分,第14小题11分,第15 小题18分,共39分。
13.一端弯曲的光滑绝缘轨道 ABN固定在竖直平面上,如图所示, AB段水平、BN段是半径为 R的半圆弧,有一个正点电荷固定在圆心O处。一质量为 m带正电小环,在水平恒力 作用下从C点由静止开始运动,到B点时撤去外力,小环继续运动,发现刚好能到达绝缘轨道上与圆心等高的 M点,已知 CB间距为 已知小环在圆轨道上时受到圆心处的点电荷的静电力大小为 2mg。求:
(1)小环从C运动到 M过程中,点电荷Q的电场力对它做的功;
(2)若水平恒力大小改为2F,则小环在能达到的最高点 N时的速度大小;
(3)小环在距离 B点 的D点以向右的初速度 运动,在静电力的作用下运动到 B点的速度恰好为0。若在 D点施加最小的恒定外力作用由静止开始运动,则小环在圆轨道上能到达的最大高度值多少?
14.如图所示, 足够长的斜面与水平面夹角为 37°,斜面上有一质量 M=3kg的长木板,斜面底端挡板高度与木板厚度相同。 m=1kg的小物块从空中某点以 v0=3m/s水平抛出,抛出同时木板由静止释放,小物块下降 h=0.8m 掉在木板前端,碰撞时间极短,可忽略不计,碰后瞬间物块垂直斜面的分速度立即变为零。碰后两者向下运动,小物块恰好在木板与挡板碰撞时在挡板处离开木板。已知木板与斜面间动摩擦因数 μ=0.5,木板上表面光滑,木板与挡板每次碰撞均无能量损失,g=10m/s2,求:
(1)碰前瞬间小物块速度大小和方向;
(2)木板至少多长小物块才没有从木板后端离开木板?
(3)木板从开始运动到最后停在斜面底端的整个过程中通过路程多大?
15.牛顿在前人研究的基础上,利用他的运动定律把行星的向心加速度与太阳对它的引力联系起来,巧妙推导出太阳和行星之间的引力关系。
(1)行星围绕太阳的运动当做匀速圆周运动,已知行星的质量为 m,太阳的质量为 M,行星与太阳中心之间的距离为 r,请利用牛顿定律和开普勒定律导出太阳和行星之间的引力表达式
(2)牛顿思考月球绕地球运行的原因时,苹果偶然落地引起了他的遐想: 拉住月球使它围绕地球运动的力与拉着苹果下落的力,是否都与太阳吸引行星的力性质相同,遵循着统一的规律:平方反比规律?因此,牛顿开始了著名的“月—地检验”。
a.已知月球与地球的距离约为地球半径的60倍,如果牛顿的猜想正确,请你据此计算月球公转的向心加速度 a和苹果下落的加速度g的比值
b.在牛顿的时代,月球与地球的距离r′、月球绕地球公转的周期T′等都能比较精确地测定,请你据此写出计算月球公转的向心加速度 a 的表达式; 已知r'≈3.84×108m, T≈2.36×106s,地面附近的重力加速度g=9.80m/s2,请你根据这些数据估算比值 a; 与(1)中的结果相比较,你能得出什么结论?
c.假如有一颗在赤道上的苹果树,长到了月亮的高度。请你根据苹果的运动状态进行受力分析,在图中的树枝上画出一个长势符合物理规律的苹果,并推断如果树冠上的苹果被人用剪刀剪离树枝,苹果是否会落回地面?(分析过程中可忽略其它星球对苹果的作用)。
同课章节目录
