华东师大版数学八年级上第14章 勾股定理 单元测试(试题+解析)
文档属性
| 名称 | 华东师大版数学八年级上第14章 勾股定理 单元测试(试题+解析) |  | |
| 格式 | zip | ||
| 文件大小 | 197.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-10-31 18:47:25 | ||
图片预览


文档简介
单元评价检测(四)
第14章
(45分钟 100分)
一、选择题(每小题4分,共28分)
1.用反证法证明命题“多边形的外角(每个顶点处取一个外角)中最多有三个钝角”时,首先应假设多边形的外角中 ( )
A.最小有三个钝角 B.最多有两个钝角
C.至少有四个钝角 D.均为钝角
【解析】选C.最多有三个钝角的反面应是至少有四个钝角.
2.如图,在4×5的方格中,A,B为两个格点,再选一个格点C,使∠ACB为直角,则满足条件的点C的个数为 ( )
( http: / / www.21cnjy.com )
A.3 B.4 C.5 D.6
【解析】选D.如图,根据勾股定理知AB2=12+32=10.
∵12+32=10,()2+(2)2=10,()2+()2=10,∴符合条件的点C有6个.
( http: / / www.21cnjy.com )
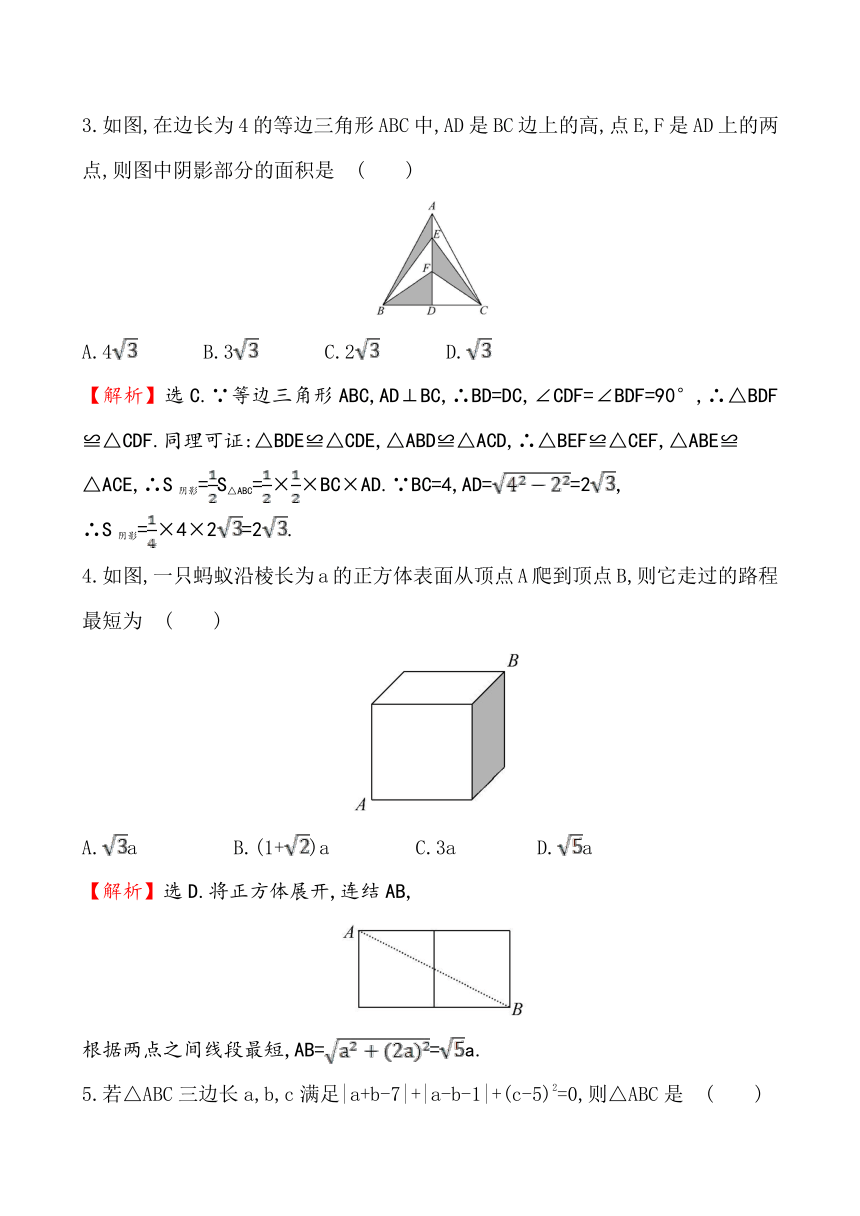
3.如图,在边长为4的等边三角形ABC中,AD是BC边上的高,点E,F是AD上的两点,则图中阴影部分的面积是 ( )
( http: / / www.21cnjy.com )
A.4 B.3 C.2 D.
【解析】选C.∵等边三角形ABC,AD⊥ ( http: / / www.21cnjy.com )BC,∴BD=DC,∠CDF=∠BDF=90°,∴△BDF≌△CDF.同理可证:△BDE≌△CDE,△ABD≌△ACD,∴△BEF≌△CEF,△ABE≌
△ACE,∴S阴影=S△ABC=××BC×AD.∵BC=4,AD==2,
∴S阴影=×4×2=2.
4.如图,一只蚂蚁沿棱长为a的正方体表面从顶点A爬到顶点B,则它走过的路程最短为 ( )
( http: / / www.21cnjy.com )
A.a B.(1+)a C.3a D.a
【解析】选D.将正方体展开,连结AB,
( http: / / www.21cnjy.com )
根据两点之间线段最短,AB==a.
5.若△ABC三边长a,b,c满足|a+b-7|+|a-b-1|+(c-5)2=0,则△ABC是 ( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
【解析】选C.依题意得:a+b-7=0 ①.
a-b-1=0 ②,
c-5=0 ③,
由②得:b=a-1 ④,
把④代入①得:a-1+a-7=0,
a=4,代入④得:b=3,由③得c=5,
∵a2+b2=c2,∴三角形ABC为直角三角形.
6.有一块边长为24m的正方形绿地ABCD ( http: / / www.21cnjy.com )(如图),在绿地的BC边上距B点7m的E处有一健身器,居住在A处的居民经常践踏绿地,沿直线AE直达E处健身,小明同学想在A处树立一块标牌“少走■米,踏之何忍 ”则标牌上的“■”处的数字是 ( )
A.5 B.6 C.7 D.8
【解析】选B.因为是一块正方形的绿地,所以 ( http: / / www.21cnjy.com )∠B=90°,由勾股定理得,AE=25m,计算由A点顺着AB,BE到E点的路程是24+7=31(m),而AE=25m,则少走31-25=6(m).
7.如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于 ( )
A. B.
C. D.
【解析】选C.连结AD,由D为BC的中点,得AD⊥BC,BD=5.在Rt△ABD中,根据勾股定理,AD==12.在△ABD中,根据三角形的面积公式,得×AD×BD=×AB×DE,所以,DE===.故选C.
二、填空题(每小题5分,共25分)
8.(2014·厦门实验质检)如图,已知在直角△ABC中,∠C=
90°,AB=5,△ABC的面积为5,则△ABC的周长为 .
【解析】设BC=a,AC=b,∵∠C=90°,AB=5,△ABC的面积为5,∴a2+b2=52=25,ab=5,∴a2+2ab+b2=(a+b)2=25+4×5=45,∴a+b==3,
因此,△ABC的周长=3+5.
答案:3+5
9.已知三角形的三边长分别是2n+1,2n2+2n,2n2+2n+1,则最大角是 .
【解析】∵(2n+1)2+(2n2+2n)2=4n4+8n3+8n2+4n+1=(2n2+2n+1)2,
∴根据勾股定理的逆定理,三角形是直角三角形,则最大角为90°.
答案:90°
10.如图,要建一个育苗棚,棚宽3.2m,高2.4m,长15m,那么覆盖在棚顶上的塑料薄膜至少需 m2.
( http: / / www.21cnjy.com )
【解析】由勾股定理知2.42+3.22=16=42,故塑料薄膜宽为4m,面积为4×15=60(m2).
答案:60
11.(2013·包头中考)如图,点E是正方形ABCD内的一点,连结AE,BE,CE,将△ABE绕点B顺时针旋转90°到
△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C= .
【解析】连结EE′,∵将△ABE绕点B顺时针旋转90°到△CBE′的位置,
AE=1,BE=2,CE=3,∴∠EBE′=90°,BE=BE′=2,AE=
E′C=1,
∴EE′=2,
∠BE′E=45°,∵E′E2+E′C2=8+1=9,EC2=9,
∴E′E2+E′C2=EC2,∴△EE′C是直角三角形,
∴∠EE′C=90°,∴∠BE′C=135°.
答案:135°
12.(2014·枣阳模拟)已知△ABC的面积为2,AB边上的高为,AB=2AC,则BC= .
【解析】如图①所示:AB=2×=4,AD==1,BD=AB-AD=3,故BC==2;如图②所示:AB=2×=4,AD==1,BD=AB+AD=5,故BC==2.
( http: / / www.21cnjy.com )
答案:2或2
三、解答题(共47分)
13.(11分)已知△ABC的三边分别为a,b,c,且a+b=4,ab=1,c=,试判定△ABC的形状,并说明理由.
【解析】△ABC是直角三角形,理由:
∵(a+b)2=16,a2+2ab+b2=16,ab=1,
∴a2+b2=14.
又∵c2=14,∴a2+b2=c2.∴△ABC是直角三角形.
14.(11分)如图,四边形ABCD是某开发区的一块空地,现计划在该空地上种上草皮,经测量∠A=90°,AB=3 m,
BC=12m,CD=13m,DA=4m.若每平方米的草皮需要200元,把这块空地全部种上草皮需要投资多少元
【解析】如图,连结BD.
在Rt△ABD中,由勾股定理,得
BD2=AB2+AD2=32+42=52.
在△DBC中,BD2+BC2=52+122=169,CD2=169.∴BD2+BC2=CD2.
∴△DBC是以CD为斜边的直角三角形.
∴S四边形ABCD=S△ABD+S△DBC
=×3×4+×5×12=36(m2).
因此,这块空地种植草皮的总投资为
200×36=7200(元).
15.(12分)(2014·丰台区一模)如图,四边形ABCD中,AB=AD,∠BAD=90°,
∠CBD=30°,∠BCD=45°,若AB=2.求四边形ABCD的面积.
( http: / / www.21cnjy.com )
【解析】如图,过点D作DE⊥BC于E,∵AB=AD,∠BAD=90°,∴AD=AB=2,BD=2×=4,∵∠CBD=30°,
∴DE=BD=×4=2,
BE===2,
∵∠BCD=45°,∴CE=DE=2,∴BC=BE+CE=2+2,∴四边形ABCD的面积=S△ABD+
S△BCD=×2×2+×(2+2)×2=4+2+2
=6+2.
( http: / / www.21cnjy.com )
16.(13分)如图,小丽 ( http: / / www.21cnjy.com )荡秋千,秋千架高2.4m,秋千座位离地0.4m,小红荡起最高时,座位离地0.8m.此时小红荡出的水平距离是多少 (荡到秋千架两边的最高点之间的距离)
( http: / / www.21cnjy.com )
【解析】如图为秋千侧面图,座位最低点为A,最高点为B,
则OA=OB=2m,过B点作OA的垂线,垂足为C,
则AC=0.8-0.4=0.4(m),OC=2-0.4=1.6(m),
由勾股定理得:BC2=OB2-OC2=22-1.62=1.22(m2),所以BC=1.2m,
所以2BC=2×1.2=2.4(m),
故小红荡出的水平距离是2.4m.
关闭Word文档返回原板块
第14章
(45分钟 100分)
一、选择题(每小题4分,共28分)
1.用反证法证明命题“多边形的外角(每个顶点处取一个外角)中最多有三个钝角”时,首先应假设多边形的外角中 ( )
A.最小有三个钝角 B.最多有两个钝角
C.至少有四个钝角 D.均为钝角
【解析】选C.最多有三个钝角的反面应是至少有四个钝角.
2.如图,在4×5的方格中,A,B为两个格点,再选一个格点C,使∠ACB为直角,则满足条件的点C的个数为 ( )
( http: / / www.21cnjy.com )
A.3 B.4 C.5 D.6
【解析】选D.如图,根据勾股定理知AB2=12+32=10.
∵12+32=10,()2+(2)2=10,()2+()2=10,∴符合条件的点C有6个.
( http: / / www.21cnjy.com )
3.如图,在边长为4的等边三角形ABC中,AD是BC边上的高,点E,F是AD上的两点,则图中阴影部分的面积是 ( )
( http: / / www.21cnjy.com )
A.4 B.3 C.2 D.
【解析】选C.∵等边三角形ABC,AD⊥ ( http: / / www.21cnjy.com )BC,∴BD=DC,∠CDF=∠BDF=90°,∴△BDF≌△CDF.同理可证:△BDE≌△CDE,△ABD≌△ACD,∴△BEF≌△CEF,△ABE≌
△ACE,∴S阴影=S△ABC=××BC×AD.∵BC=4,AD==2,
∴S阴影=×4×2=2.
4.如图,一只蚂蚁沿棱长为a的正方体表面从顶点A爬到顶点B,则它走过的路程最短为 ( )
( http: / / www.21cnjy.com )
A.a B.(1+)a C.3a D.a
【解析】选D.将正方体展开,连结AB,
( http: / / www.21cnjy.com )
根据两点之间线段最短,AB==a.
5.若△ABC三边长a,b,c满足|a+b-7|+|a-b-1|+(c-5)2=0,则△ABC是 ( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
【解析】选C.依题意得:a+b-7=0 ①.
a-b-1=0 ②,
c-5=0 ③,
由②得:b=a-1 ④,
把④代入①得:a-1+a-7=0,
a=4,代入④得:b=3,由③得c=5,
∵a2+b2=c2,∴三角形ABC为直角三角形.
6.有一块边长为24m的正方形绿地ABCD ( http: / / www.21cnjy.com )(如图),在绿地的BC边上距B点7m的E处有一健身器,居住在A处的居民经常践踏绿地,沿直线AE直达E处健身,小明同学想在A处树立一块标牌“少走■米,踏之何忍 ”则标牌上的“■”处的数字是 ( )
A.5 B.6 C.7 D.8
【解析】选B.因为是一块正方形的绿地,所以 ( http: / / www.21cnjy.com )∠B=90°,由勾股定理得,AE=25m,计算由A点顺着AB,BE到E点的路程是24+7=31(m),而AE=25m,则少走31-25=6(m).
7.如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于 ( )
A. B.
C. D.
【解析】选C.连结AD,由D为BC的中点,得AD⊥BC,BD=5.在Rt△ABD中,根据勾股定理,AD==12.在△ABD中,根据三角形的面积公式,得×AD×BD=×AB×DE,所以,DE===.故选C.
二、填空题(每小题5分,共25分)
8.(2014·厦门实验质检)如图,已知在直角△ABC中,∠C=
90°,AB=5,△ABC的面积为5,则△ABC的周长为 .
【解析】设BC=a,AC=b,∵∠C=90°,AB=5,△ABC的面积为5,∴a2+b2=52=25,ab=5,∴a2+2ab+b2=(a+b)2=25+4×5=45,∴a+b==3,
因此,△ABC的周长=3+5.
答案:3+5
9.已知三角形的三边长分别是2n+1,2n2+2n,2n2+2n+1,则最大角是 .
【解析】∵(2n+1)2+(2n2+2n)2=4n4+8n3+8n2+4n+1=(2n2+2n+1)2,
∴根据勾股定理的逆定理,三角形是直角三角形,则最大角为90°.
答案:90°
10.如图,要建一个育苗棚,棚宽3.2m,高2.4m,长15m,那么覆盖在棚顶上的塑料薄膜至少需 m2.
( http: / / www.21cnjy.com )
【解析】由勾股定理知2.42+3.22=16=42,故塑料薄膜宽为4m,面积为4×15=60(m2).
答案:60
11.(2013·包头中考)如图,点E是正方形ABCD内的一点,连结AE,BE,CE,将△ABE绕点B顺时针旋转90°到
△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C= .
【解析】连结EE′,∵将△ABE绕点B顺时针旋转90°到△CBE′的位置,
AE=1,BE=2,CE=3,∴∠EBE′=90°,BE=BE′=2,AE=
E′C=1,
∴EE′=2,
∠BE′E=45°,∵E′E2+E′C2=8+1=9,EC2=9,
∴E′E2+E′C2=EC2,∴△EE′C是直角三角形,
∴∠EE′C=90°,∴∠BE′C=135°.
答案:135°
12.(2014·枣阳模拟)已知△ABC的面积为2,AB边上的高为,AB=2AC,则BC= .
【解析】如图①所示:AB=2×=4,AD==1,BD=AB-AD=3,故BC==2;如图②所示:AB=2×=4,AD==1,BD=AB+AD=5,故BC==2.
( http: / / www.21cnjy.com )
答案:2或2
三、解答题(共47分)
13.(11分)已知△ABC的三边分别为a,b,c,且a+b=4,ab=1,c=,试判定△ABC的形状,并说明理由.
【解析】△ABC是直角三角形,理由:
∵(a+b)2=16,a2+2ab+b2=16,ab=1,
∴a2+b2=14.
又∵c2=14,∴a2+b2=c2.∴△ABC是直角三角形.
14.(11分)如图,四边形ABCD是某开发区的一块空地,现计划在该空地上种上草皮,经测量∠A=90°,AB=3 m,
BC=12m,CD=13m,DA=4m.若每平方米的草皮需要200元,把这块空地全部种上草皮需要投资多少元
【解析】如图,连结BD.
在Rt△ABD中,由勾股定理,得
BD2=AB2+AD2=32+42=52.
在△DBC中,BD2+BC2=52+122=169,CD2=169.∴BD2+BC2=CD2.
∴△DBC是以CD为斜边的直角三角形.
∴S四边形ABCD=S△ABD+S△DBC
=×3×4+×5×12=36(m2).
因此,这块空地种植草皮的总投资为
200×36=7200(元).
15.(12分)(2014·丰台区一模)如图,四边形ABCD中,AB=AD,∠BAD=90°,
∠CBD=30°,∠BCD=45°,若AB=2.求四边形ABCD的面积.
( http: / / www.21cnjy.com )
【解析】如图,过点D作DE⊥BC于E,∵AB=AD,∠BAD=90°,∴AD=AB=2,BD=2×=4,∵∠CBD=30°,
∴DE=BD=×4=2,
BE===2,
∵∠BCD=45°,∴CE=DE=2,∴BC=BE+CE=2+2,∴四边形ABCD的面积=S△ABD+
S△BCD=×2×2+×(2+2)×2=4+2+2
=6+2.
( http: / / www.21cnjy.com )
16.(13分)如图,小丽 ( http: / / www.21cnjy.com )荡秋千,秋千架高2.4m,秋千座位离地0.4m,小红荡起最高时,座位离地0.8m.此时小红荡出的水平距离是多少 (荡到秋千架两边的最高点之间的距离)
( http: / / www.21cnjy.com )
【解析】如图为秋千侧面图,座位最低点为A,最高点为B,
则OA=OB=2m,过B点作OA的垂线,垂足为C,
则AC=0.8-0.4=0.4(m),OC=2-0.4=1.6(m),
由勾股定理得:BC2=OB2-OC2=22-1.62=1.22(m2),所以BC=1.2m,
所以2BC=2×1.2=2.4(m),
故小红荡出的水平距离是2.4m.
关闭Word文档返回原板块
