人教版数学八年级上册 14.2.1 平方差公式 课件(共33张PPT)
文档属性
| 名称 | 人教版数学八年级上册 14.2.1 平方差公式 课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-19 00:00:00 | ||
图片预览





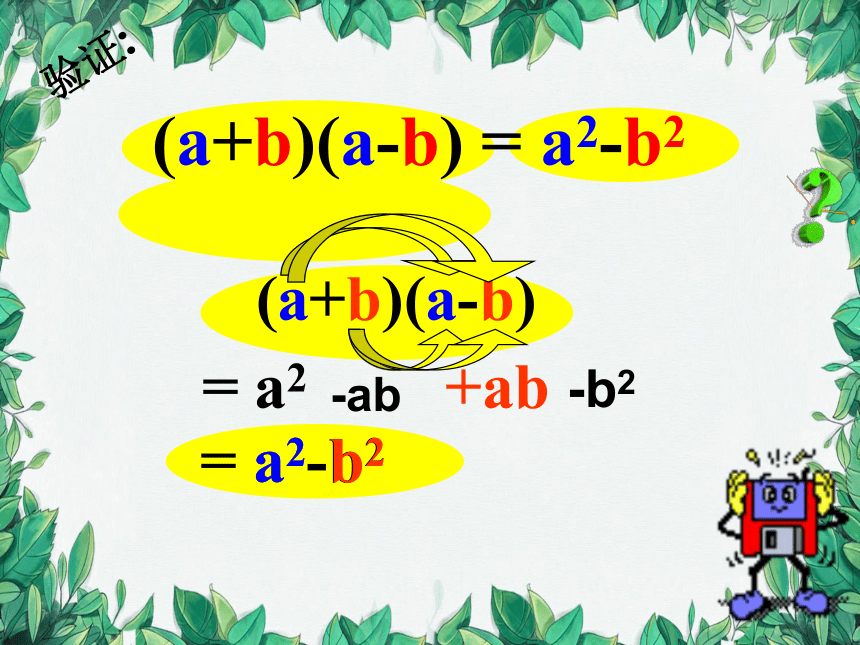


文档简介
(共33张PPT)
以前,狡猾的灰太狼,把一块长为a米的正方形土地租给懒羊羊种植。今年,他对懒羊羊说:“我把你这块地一边减少4米,另一边增加4米,继续租给你,你也没有吃亏,你看如何?”懒羊羊听了,觉得好像没有吃亏,就答应了。懒羊羊回去羊村,把这件事跟大伙一说,喜羊羊马上就说懒羊羊吃亏了。过了一会儿沸羊羊也说懒羊羊确实吃亏了。这是为什么呢?
喜羊羊与灰太狼
小故事
4米
4米
a米
(a-4)
(a+4)米
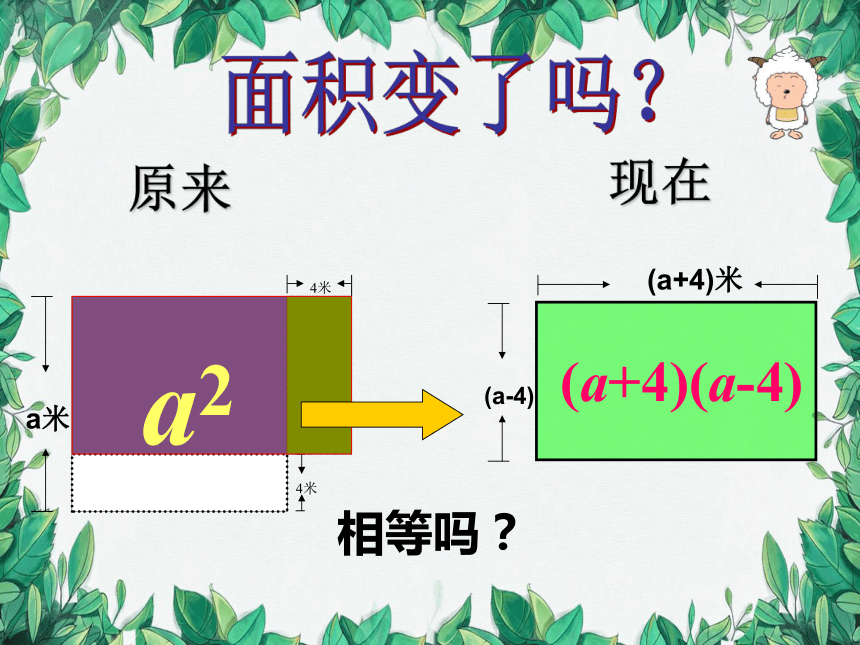
相等吗?
原来
现在
a2
(a+4)(a-4)
14.2.1
1.经历探索平方差公式的过程,会推导平方差公式。
2.理解探索平方差公式的几何意义。
3.理解平方差公式的结构特征,灵活应用平方差公式。
多项式与多项式是如何相乘的?
探究:
计算下列多项式的积:
(x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =
x2 - 1
m2 - 4
4x2 - 1
你发现什么规律了
猜想:
(a+b)(a-b) =
a2-b2
(a+b)(a-b) = a2-b2
验证:
(a+b)(a-b)
= a2
+ab
= a2-b2
a2
b2
-ab
-b2
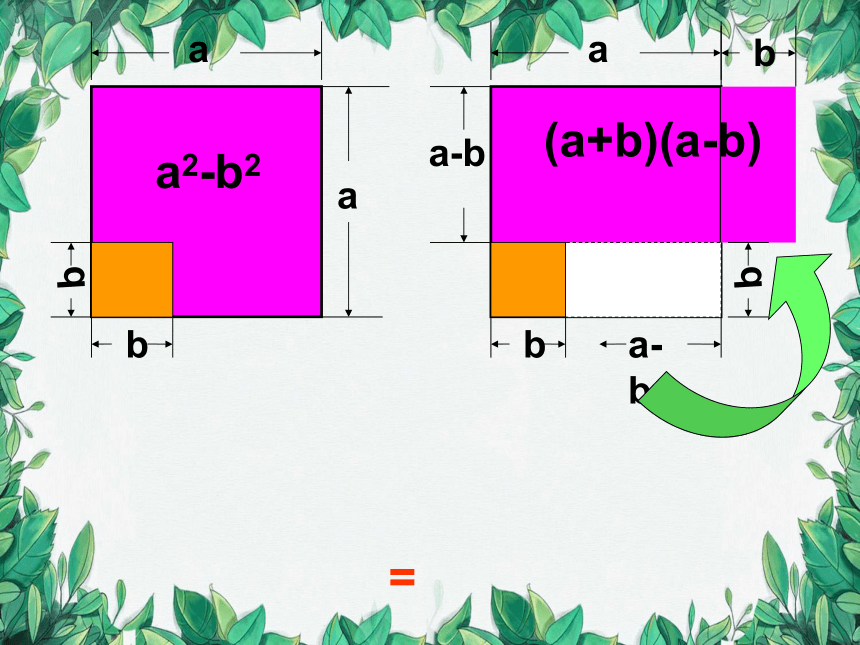
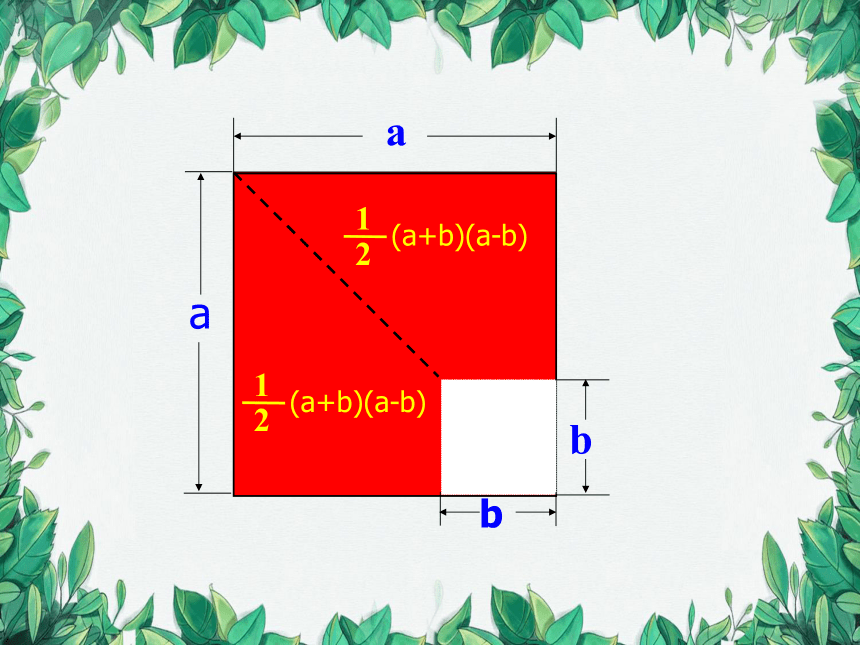
刚才我们用多项式乘法验证了平方差公式的正确性,它还可以用几何的方法加以说明呢。
思考:
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
=
a-b
a-b
b
a
a
b
1
2
(a+b)(a-b)
1
2
(a+b)(a-b)
b
a
a
b
(a+b)(a-b)
=
a2-b2
(a+b)(a-b)=a2-b2
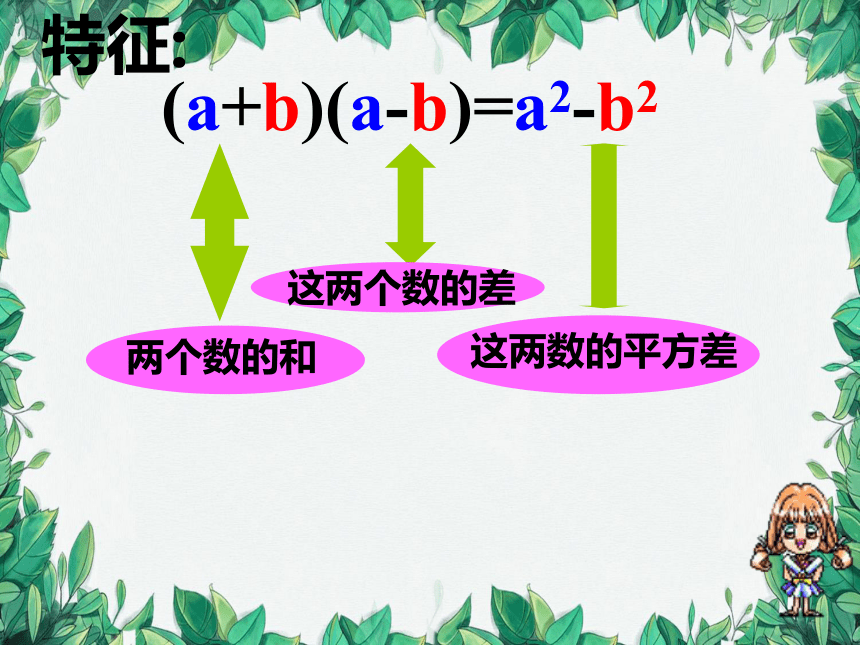
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
相同
(a+b)(a-b)=a2-b2
特征:
相反数
(a+b)(a-b)=a2-b2
特征:
平方差
(a+b)(a-b)=a2-b2
特征:
(相同项)2-(相反项)2
(a+b)(a-b) a
(相同) b
(相反) a2-b2
(平方差) 最后结果
(2x+2)(2x-2)
(m+3n)(3n-m)
(-a+4b)(-a-4b)
2x
3n
-a
m
4b
(3n)2-m2
(-a)2- (4b)2
4x2-4
a2-16b2
9n2-m2
2
(2x)2-22
例1 运用平方差公式计算:
⑴ (3x+2)(3x-2) ;
⑵ (b+2a)(2a-b);
(3) (-x+2y)(-x-2y).
分析:
⑴ (3x+2)(3x-2)
3x
3x
a
a
2
2
b
b
(
+
)
(
-
)
= a2 - b2
=
(3x)2
-
22
你知道吗?
用公式关键是识别两数
完全相同项 — a
互为相反数项— b
解:
⑴ (3x+2)(3x-2)
=
(3x)2
3x
3x
-
2
2
22
= 9x2 - 4
⑵ (b+2a)(2a-b);
b
-b
+2a
2a
=(2a+b)(2a-b)
2a
2a
=(2a)2
=4a2 – b2
b
b
-
b2
要认真呀!
位置变化!
(3) (-x+2y)(-x-2y)
= (-x)2-(2y)2
= x2-4y2
ㄨ
下面各式的计算对不对?
如果不对,应当怎样改正?
(1) (x+2)(x-2) = x2 - 2
(2) (-3a-2)(3a-2) = 9a2 - 4
X2 - 4
ㄨ
4 - 9a2
运用平方差公式计算:
(1) (a+3b)(a-3b) =
a2 - 9b2
(2) (3+2a)(-3+2a) =
4a2 - 9
例2 计算:
⑴ 102 ×98;
⑵ (y+2)(y-2)-(y-1)(y+5);
⑴ 102 ×98
动 脑筋!
谁是a
谁是b
102
= (100+2)
98
(100-2)
= 1002-22
= 10000-4
= 9996
⑵ (y+2)(y-2)-(y-1)(y+5)
动 脑筋!
y
y
y
y
2
2
= y2 - 22
1
5
- (y2+4y-5)
= y2-4-y2-4y+5
= -4y+1
我能行!
运用平方差公式计算:
1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
2499
无中生有
(a+b)(a-b)=a2-b2
课堂小结
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用
灵活运用平方差公式计算:
1、(3x+4)(3x-4) – (2x+3)(3x-2);
2、(x+y)(x-y)(x2+y2);
(2+1)(22+1)(24+1)
喜羊羊同学在计算(2+1)(22+1)(24+1)时,
将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1)
= (22-1)(22+1)(24+1)
= (24-1)(24+1)
= 28-1
你能根据上题计算:
(2+1)(22+1)(24+1)(28+1) … (22n+1) 的结果吗?
以前,狡猾的灰太狼,把一块长为a米的正方形土地租给懒羊羊种植。今年,他对懒羊羊说:“我把你这块地一边减少4米,另一边增加4米,继续租给你,你也没有吃亏,你看如何?”懒羊羊听了,觉得好像没有吃亏,就答应了。懒羊羊回去羊村,把这件事跟大伙一说,喜羊羊马上就说懒羊羊吃亏了。过了一会儿沸羊羊也说懒羊羊确实吃亏了。这是为什么呢?
喜羊羊与灰太狼
小故事
4米
4米
a米
(a-4)
(a+4)米
相等吗?
原来
现在
a2
(a+4)(a-4)
14.2.1
1.经历探索平方差公式的过程,会推导平方差公式。
2.理解探索平方差公式的几何意义。
3.理解平方差公式的结构特征,灵活应用平方差公式。
多项式与多项式是如何相乘的?
探究:
计算下列多项式的积:
(x+1)(x-1) =
(m+2)(m-2) =
(2x+1)(2x-1) =
x2 - 1
m2 - 4
4x2 - 1
你发现什么规律了
猜想:
(a+b)(a-b) =
a2-b2
(a+b)(a-b) = a2-b2
验证:
(a+b)(a-b)
= a2
+ab
= a2-b2
a2
b2
-ab
-b2
刚才我们用多项式乘法验证了平方差公式的正确性,它还可以用几何的方法加以说明呢。
思考:
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
=
a-b
a-b
b
a
a
b
1
2
(a+b)(a-b)
1
2
(a+b)(a-b)
b
a
a
b
(a+b)(a-b)
=
a2-b2
(a+b)(a-b)=a2-b2
特征:
两个数的和
这两个数的差
这两数的平方差
(a+b)(a-b)=a2-b2
特征:
相同
(a+b)(a-b)=a2-b2
特征:
相反数
(a+b)(a-b)=a2-b2
特征:
平方差
(a+b)(a-b)=a2-b2
特征:
(相同项)2-(相反项)2
(a+b)(a-b) a
(相同) b
(相反) a2-b2
(平方差) 最后结果
(2x+2)(2x-2)
(m+3n)(3n-m)
(-a+4b)(-a-4b)
2x
3n
-a
m
4b
(3n)2-m2
(-a)2- (4b)2
4x2-4
a2-16b2
9n2-m2
2
(2x)2-22
例1 运用平方差公式计算:
⑴ (3x+2)(3x-2) ;
⑵ (b+2a)(2a-b);
(3) (-x+2y)(-x-2y).
分析:
⑴ (3x+2)(3x-2)
3x
3x
a
a
2
2
b
b
(
+
)
(
-
)
= a2 - b2
=
(3x)2
-
22
你知道吗?
用公式关键是识别两数
完全相同项 — a
互为相反数项— b
解:
⑴ (3x+2)(3x-2)
=
(3x)2
3x
3x
-
2
2
22
= 9x2 - 4
⑵ (b+2a)(2a-b);
b
-b
+2a
2a
=(2a+b)(2a-b)
2a
2a
=(2a)2
=4a2 – b2
b
b
-
b2
要认真呀!
位置变化!
(3) (-x+2y)(-x-2y)
= (-x)2-(2y)2
= x2-4y2
ㄨ
下面各式的计算对不对?
如果不对,应当怎样改正?
(1) (x+2)(x-2) = x2 - 2
(2) (-3a-2)(3a-2) = 9a2 - 4
X2 - 4
ㄨ
4 - 9a2
运用平方差公式计算:
(1) (a+3b)(a-3b) =
a2 - 9b2
(2) (3+2a)(-3+2a) =
4a2 - 9
例2 计算:
⑴ 102 ×98;
⑵ (y+2)(y-2)-(y-1)(y+5);
⑴ 102 ×98
动 脑筋!
谁是a
谁是b
102
= (100+2)
98
(100-2)
= 1002-22
= 10000-4
= 9996
⑵ (y+2)(y-2)-(y-1)(y+5)
动 脑筋!
y
y
y
y
2
2
= y2 - 22
1
5
- (y2+4y-5)
= y2-4-y2-4y+5
= -4y+1
我能行!
运用平方差公式计算:
1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
2499
无中生有
(a+b)(a-b)=a2-b2
课堂小结
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
1.符号表示:(a+b)(a-b)=a2-b2
2.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用
灵活运用平方差公式计算:
1、(3x+4)(3x-4) – (2x+3)(3x-2);
2、(x+y)(x-y)(x2+y2);
(2+1)(22+1)(24+1)
喜羊羊同学在计算(2+1)(22+1)(24+1)时,
将积式乘以(2-1)得:
解:原式 = (2-1)(2+1)(22+1)(24+1)
= (22-1)(22+1)(24+1)
= (24-1)(24+1)
= 28-1
你能根据上题计算:
(2+1)(22+1)(24+1)(28+1) … (22n+1) 的结果吗?
