8.1认识不等式[下学期]
图片预览








文档简介
课件22张PPT。8.1认识不等式
教学目标:
知识目标:
通过对实际问题中的分析,引入不等式概念,使 学生初步了解不等式及解集的意义
能力目标:
通过对问题的探索,适当渗透变量知识,使学生 感受到其中的函数思想,让学生发现不等式的解与方程的解的之间的区别
情感目标:
通过不等式的学习,让学生认识到事物间的区别和联系
教学重点:
不等式及解的意义 教学难点:
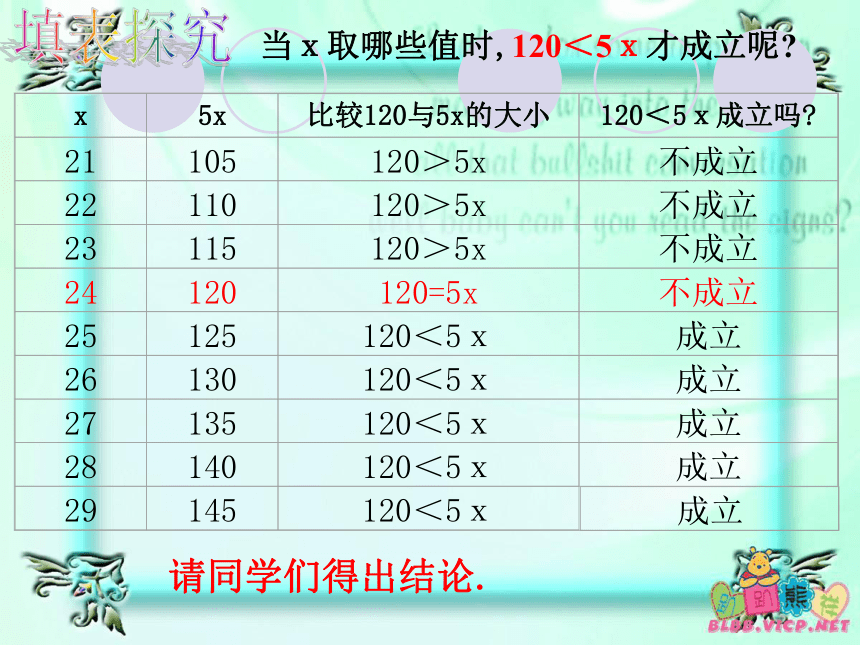
不等式解的理解x取哪些数值时,120<5x成立?当x取哪些值时,120<5x才成立呢? x
5x
比较120与5x的大小
120<5x成立吗?
21
105
120>5x
不成立
22
110
120>5x
不成立
23
115
120>5x
不成立
24
120
120=5x
不成立
25
125
120<5x
成立
26
130
120<5x
成立
27
135
120<5x
成立
28
140
120<5x
成立
29
145
120<5x
成立
填表探究请同学们得出结论. 唉,我还是老样子,仍旧6kg。
设唐老鸭现在体重为xkg,你能用简单的数学式
子表示它们之间的体重关系吗?X <6那我比较轻探究新知
(1)公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40Km/h,用v(Km/h)表示汽车的速度,怎样表示v和40之间的关系?v ≤40探究新知(3)根据科学家测定,太阳表面的温度不低于6000℃.设太阳表面的温度为t(℃),怎样表示t和6000之间的关系?t ≥6000探究新知3x >5(3)如图5-2,天平左盘放3个乒乓球,右盘放5g砝码,天平倾斜。设每个乒乓球的质量为x(g),怎样表示x与5之间的关系? 观察由上述几个问题中得到
的关系式,它们有什么共同
的特点?
x<6, t 6000, v 40, 3x >5, 思考< 小于
> 大于
≤ 小于或等于
≥ 大于或等于
(不大于、 )(不小于、 ) x<6, v ≤40 ,3x >5, 至多至少你能理解吗?阅读教材第41页,理解不等式和不等式的解的意义。你来猜猜看?1、判断下列各式中哪些是不等式:
⑴ x+1=2 ⑵ 0>-3 ⑶ x-6
⑷ ⑸ x +2 y-3 (2)、(4)、(5)(2) y-4例:用不等式表示下列关系,(1)x的一半小于-1;
(2)y与4的差大于3;
( 3) a是负数 ; ( 4) b是非负数 ;解(1) > 3 (3) a<0 . (4) b≥0 <-12.根据所给条件中的不等关系,确定不等号.1.根据所给条件中的关系语确定不等式两边的代数式;注意x选择题
1.a的相反数与1的和不是正数,用不等式表示为( )
C2. x、y两数的平方差不大于0,用不等式表示为( )
D判断 (1) y与2的差是正数,可表示为y-2<0. ( )(2) b的 与c的和是负数,可表示为 b+c<0 ( )+√(3) x的2倍大于x, 可表示为 ( )√算一算2.下列各数中,哪些是不等式
x+2>5的解?哪些不是?
-3,-2,-1,0, 1.5, 2.5, 3, 3.5, 5, 7.小结:
认识了“不等式”
2. 认识了“不等式的解”
3.在解题过程中,一定要注意“非正数”、“非负数”、
“不大于”、、“不小于”、“至多”、“至少”等数学术语。
作业:
书本42页习题8.1:1,2,3
练习册35页
教学目标:
知识目标:
通过对实际问题中的分析,引入不等式概念,使 学生初步了解不等式及解集的意义
能力目标:
通过对问题的探索,适当渗透变量知识,使学生 感受到其中的函数思想,让学生发现不等式的解与方程的解的之间的区别
情感目标:
通过不等式的学习,让学生认识到事物间的区别和联系
教学重点:
不等式及解的意义 教学难点:
不等式解的理解x取哪些数值时,120<5x成立?当x取哪些值时,120<5x才成立呢? x
5x
比较120与5x的大小
120<5x成立吗?
21
105
120>5x
不成立
22
110
120>5x
不成立
23
115
120>5x
不成立
24
120
120=5x
不成立
25
125
120<5x
成立
26
130
120<5x
成立
27
135
120<5x
成立
28
140
120<5x
成立
29
145
120<5x
成立
填表探究请同学们得出结论. 唉,我还是老样子,仍旧6kg。
设唐老鸭现在体重为xkg,你能用简单的数学式
子表示它们之间的体重关系吗?X <6那我比较轻探究新知
(1)公路上对汽车的限速标志,表示汽车在该路段行使的速度不得超过40Km/h,用v(Km/h)表示汽车的速度,怎样表示v和40之间的关系?v ≤40探究新知(3)根据科学家测定,太阳表面的温度不低于6000℃.设太阳表面的温度为t(℃),怎样表示t和6000之间的关系?t ≥6000探究新知3x >5(3)如图5-2,天平左盘放3个乒乓球,右盘放5g砝码,天平倾斜。设每个乒乓球的质量为x(g),怎样表示x与5之间的关系? 观察由上述几个问题中得到
的关系式,它们有什么共同
的特点?
x<6, t 6000, v 40, 3x >5, 思考< 小于
> 大于
≤ 小于或等于
≥ 大于或等于
(不大于、 )(不小于、 ) x<6, v ≤40 ,3x >5, 至多至少你能理解吗?阅读教材第41页,理解不等式和不等式的解的意义。你来猜猜看?1、判断下列各式中哪些是不等式:
⑴ x+1=2 ⑵ 0>-3 ⑶ x-6
⑷ ⑸ x +2 y-3 (2)、(4)、(5)(2) y-4例:用不等式表示下列关系,(1)x的一半小于-1;
(2)y与4的差大于3;
( 3) a是负数 ; ( 4) b是非负数 ;解(1) > 3 (3) a<0 . (4) b≥0 <-12.根据所给条件中的不等关系,确定不等号.1.根据所给条件中的关系语确定不等式两边的代数式;注意x选择题
1.a的相反数与1的和不是正数,用不等式表示为( )
C2. x、y两数的平方差不大于0,用不等式表示为( )
D判断 (1) y与2的差是正数,可表示为y-2<0. ( )(2) b的 与c的和是负数,可表示为 b+c<0 ( )+√(3) x的2倍大于x, 可表示为 ( )√算一算2.下列各数中,哪些是不等式
x+2>5的解?哪些不是?
-3,-2,-1,0, 1.5, 2.5, 3, 3.5, 5, 7.小结:
认识了“不等式”
2. 认识了“不等式的解”
3.在解题过程中,一定要注意“非正数”、“非负数”、
“不大于”、、“不小于”、“至多”、“至少”等数学术语。
作业:
书本42页习题8.1:1,2,3
练习册35页
