8.2.2不等式的简单变形[下学期]
文档属性
| 名称 | 8.2.2不等式的简单变形[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 120.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-06 00:00:00 | ||
图片预览






文档简介
课件19张PPT。不等式的简单变形让我们先做个实验吧!如图所示,一个倾斜的天平两边分别放有重物,其质量分别为a和b(显然a>b),如果在两边盘内分别加上等量的砝码c,那么盘子仍然像原来那样倾斜 即a+c>b+c 用“>” “<” 或“ = ”填空,并就此说说你的想法
(1)8﹍﹍4
(2)8-2﹍﹍4 -2 (3)8+3﹍﹍4+3
(4)8×2﹍﹍ 4×2(5)8÷2 ﹍﹍ 4÷2
(6)8× (-2) ﹍﹍ 4× (-2)
(7) 8÷ (-2) ﹍﹍ 4÷( -2)
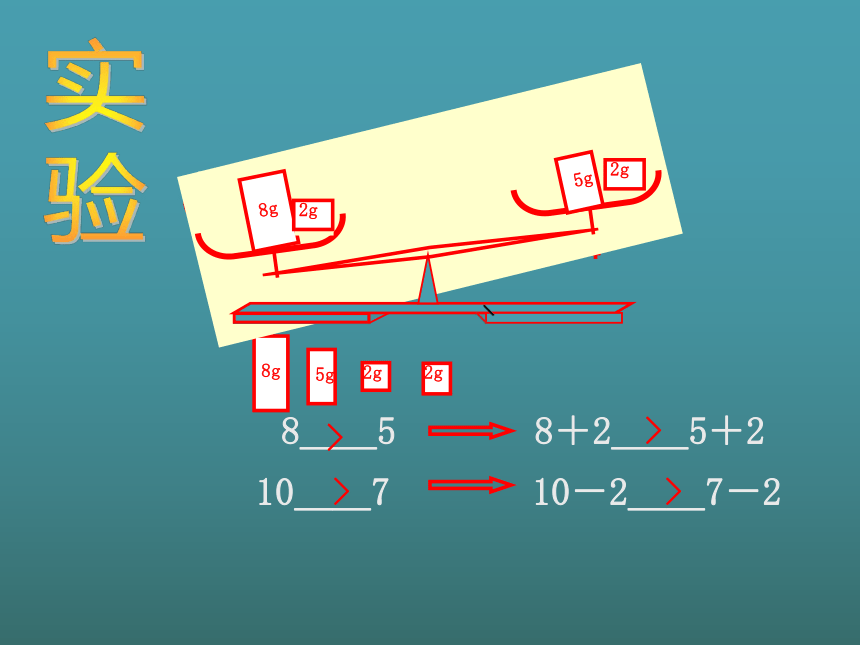
(9)8× 0 ﹍﹍ 4× 0 > >>>><<=你发现了什么?实
验8__58+2__5+210__710-2__7-2>>>>复习提问(1)天平被调整到什么状态?(2)给不平衡的天平两边同时加入相同质量的砝码,天平会有什么变化?(3)不平衡的天平两边同时拿掉相同质量的砝码,天平会有什么变化?(4)如果对不平衡的天平两边砝码的质量同时扩大相同的倍数,天平会平衡吗?缩小相同的倍数呢?探究新知1、用“>”或“<”填空:
(1)- 1<3 -1+2 3+2 -1-3 3-3
(2) 5>3 5+a 3+a 5-a 3-a
(3) 6>2 6×5 2×5 6×(-5) 2×(-5)
(4) –2<3 (-2)×6 3×6 (-2)(-6) 3×(-6)
(5)-4>-6 (-4)÷2 (-6)÷2
(-4)÷(-2) (-6)÷(-2)<<>>><<>><2、从以上的练习中,你发现了什么?请你再用几个例子试一试,还有类似的结论吗?结论:不等式的性质1:如果a>b,那么a+c>b+c,a-c>b-c 这就是说,不等式的两边都加上(或减去)同一个数或同一个整式,不等式的方向不变。 (1)不等式两边都加上(或减去)同一个数或同一个整式,不等号方向如何变化?
归 纳不等式性质1:不等式两边都加上(或减去)同一个数(或一个式子),不等号的方向不变。不等式性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变。不等式性质3:不等式两边都乘(或除以)同一个负数,不等号的方向改变。如果 , ,那么 bc
(或 )如果 , ,那么 bc
(或 )如果 ,那么 >>><<巩固新知1、判断:
(1)∵ a < b ∴ a – b < b – b ( )
(2)∵ a < b ∴ ( )
(3)∵ a < b ∴ - 2 a < - 2 b ( )
(4)∵ - 2 a > 0 ∴ a > 0 ( )
(5) ∵ - a < - 3 ∴ a < 3 ( )2、填空:
(1)∵ 2 a > 3 a ∴ a是 数
(2) ∵ ∴ a是 数
(3) ∵ a x < a 且x > 1 ∴ a是 数负正负3、根据下列已知条件,说出a与b的不等关系,并说明是根据不等式哪一个性质:
(1) (2)
(3)思考题1、已知 a < - 1 ,则下列不等式中错误的是( )A、4a < - 4 B、- 4a < 4 C、a + 2 < 1 D、2 – a > 32、已知x < y,下列哪些不等式成立?
(1) x – 3 < y – 3 (2)- 5 x < - 5 y
(3) - 3 x +2 < - 3 y + 2 (4)- 3 x + 2 > - 3y + 2 3、已知a>b,若a<0,则a2 ab;若a>0,则a2 ab. 4、下列各式分别在什么条件下成立?
(1) a > - a (2) a2 > aB<>例2.设a>b,用“<”或“>”填空:
(1)a-3 b-3 (2) (3) -4a -4b不等式和它的基本性质>><不等式和它的基本性质
1.用“>”或“<”在横线上填空,并在题后
括号内填写理由.
∵a>b (2)∵ a>b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m>5n (4)∵4x>5x
∴ -m ( ) ∴ x 0( )
(5)∵ < (6)∵a-1<8
∴ a 2b( ) ∴ a 9( ) >>><<<不等式基
本性质1不等式基
本性质3不等式基
本性质3不等式基
本性质1不等式基
本性质2不等式基
本性质1不等式和它的基本性质判断正误:
(1)∵a+8>4 (2)∵3>2
∴a>-4 ( ) ∴3a>2a( )
(3)∵-1>-2 (4)∵ab>0
∴a-1>a-2 ( ) ∴a>0,b> 0( )√×√×与解方程一样,解不等式的过程,就是要将不等式变形成x>a或x(1)x-7<8 解 :不等式的两边都加上7,不等式的方向不变,所以x-7+7<8+7, 得 x<15 (2)3x<2x-3例2:(2)-2x<6
解不等式:
(1) x>-3; 小结:作业:练习册
(1)8﹍﹍4
(2)8-2﹍﹍4 -2 (3)8+3﹍﹍4+3
(4)8×2﹍﹍ 4×2(5)8÷2 ﹍﹍ 4÷2
(6)8× (-2) ﹍﹍ 4× (-2)
(7) 8÷ (-2) ﹍﹍ 4÷( -2)
(9)8× 0 ﹍﹍ 4× 0 > >>>><<=你发现了什么?实
验8__58+2__5+210__710-2__7-2>>>>复习提问(1)天平被调整到什么状态?(2)给不平衡的天平两边同时加入相同质量的砝码,天平会有什么变化?(3)不平衡的天平两边同时拿掉相同质量的砝码,天平会有什么变化?(4)如果对不平衡的天平两边砝码的质量同时扩大相同的倍数,天平会平衡吗?缩小相同的倍数呢?探究新知1、用“>”或“<”填空:
(1)- 1<3 -1+2 3+2 -1-3 3-3
(2) 5>3 5+a 3+a 5-a 3-a
(3) 6>2 6×5 2×5 6×(-5) 2×(-5)
(4) –2<3 (-2)×6 3×6 (-2)(-6) 3×(-6)
(5)-4>-6 (-4)÷2 (-6)÷2
(-4)÷(-2) (-6)÷(-2)<<>>><<>><2、从以上的练习中,你发现了什么?请你再用几个例子试一试,还有类似的结论吗?结论:不等式的性质1:如果a>b,那么a+c>b+c,a-c>b-c 这就是说,不等式的两边都加上(或减去)同一个数或同一个整式,不等式的方向不变。 (1)不等式两边都加上(或减去)同一个数或同一个整式,不等号方向如何变化?
归 纳不等式性质1:不等式两边都加上(或减去)同一个数(或一个式子),不等号的方向不变。不等式性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变。不等式性质3:不等式两边都乘(或除以)同一个负数,不等号的方向改变。如果 , ,那么 bc
(或 )如果 , ,那么 bc
(或 )如果 ,那么 >>><<巩固新知1、判断:
(1)∵ a < b ∴ a – b < b – b ( )
(2)∵ a < b ∴ ( )
(3)∵ a < b ∴ - 2 a < - 2 b ( )
(4)∵ - 2 a > 0 ∴ a > 0 ( )
(5) ∵ - a < - 3 ∴ a < 3 ( )2、填空:
(1)∵ 2 a > 3 a ∴ a是 数
(2) ∵ ∴ a是 数
(3) ∵ a x < a 且x > 1 ∴ a是 数负正负3、根据下列已知条件,说出a与b的不等关系,并说明是根据不等式哪一个性质:
(1) (2)
(3)思考题1、已知 a < - 1 ,则下列不等式中错误的是( )A、4a < - 4 B、- 4a < 4 C、a + 2 < 1 D、2 – a > 32、已知x < y,下列哪些不等式成立?
(1) x – 3 < y – 3 (2)- 5 x < - 5 y
(3) - 3 x +2 < - 3 y + 2 (4)- 3 x + 2 > - 3y + 2 3、已知a>b,若a<0,则a2 ab;若a>0,则a2 ab. 4、下列各式分别在什么条件下成立?
(1) a > - a (2) a2 > aB<>例2.设a>b,用“<”或“>”填空:
(1)a-3 b-3 (2) (3) -4a -4b不等式和它的基本性质>><不等式和它的基本性质
1.用“>”或“<”在横线上填空,并在题后
括号内填写理由.
∵a>b (2)∵ a>b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m>5n (4)∵4x>5x
∴ -m ( ) ∴ x 0( )
(5)∵ < (6)∵a-1<8
∴ a 2b( ) ∴ a 9( ) >>><<<不等式基
本性质1不等式基
本性质3不等式基
本性质3不等式基
本性质1不等式基
本性质2不等式基
本性质1不等式和它的基本性质判断正误:
(1)∵a+8>4 (2)∵3>2
∴a>-4 ( ) ∴3a>2a( )
(3)∵-1>-2 (4)∵ab>0
∴a-1>a-2 ( ) ∴a>0,b> 0( )√×√×与解方程一样,解不等式的过程,就是要将不等式变形成x>a或x
解不等式:
(1) x>-3; 小结:作业:练习册
