四川省雅安市2022-2023学年高二下学期期末检测数学(文)试题(含答案)
文档属性
| 名称 | 四川省雅安市2022-2023学年高二下学期期末检测数学(文)试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 491.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 01:06:49 | ||
图片预览



文档简介
雅安市2022-2023学年高二下学期期末检测
(文科)数学试题
(本试卷满分150分,答题时间120分钟)
注意事项:
1.答题前,考生务必将自己的姓名、考号用0.5毫米的黑色墨迹签字笔填写在答题卡上,并检查条形码粘贴是否正确.
2.选择题使用2B铅笔填涂在答题卡对应题目标号的位置上;非选择题用0.5毫米黑色墨迹签字笔书写在答题卡的对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.
3.考试结束后,将答题卡收回.
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求的.
1.已知,则复数在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知集合,,则( )
A. B. C. D.
3.设函数则( )
A.1 B.2 C.4 D.8
4.函数的定义域是( )
A. B. C. D.
5.已知命题:,;命题:直线:与:相互垂直的充要条件为,则下列命题中为真命题的是( )
A. B. C. D.
6.下列说法中正确的是( )
A.“”是“”成立的充分不必要条件
B.命题:,,则,,
C.在研究成对数据的相关关系时,相关关系越强,相关系数越接近于1
D.已知样本点()组成一个样本,得到回归直线方程,且,剔除两个样本点和得到新的回归直线的斜率为3,则新的回归方程为
7.当时,函数取得最小值1,则( )
A. B. C. D.
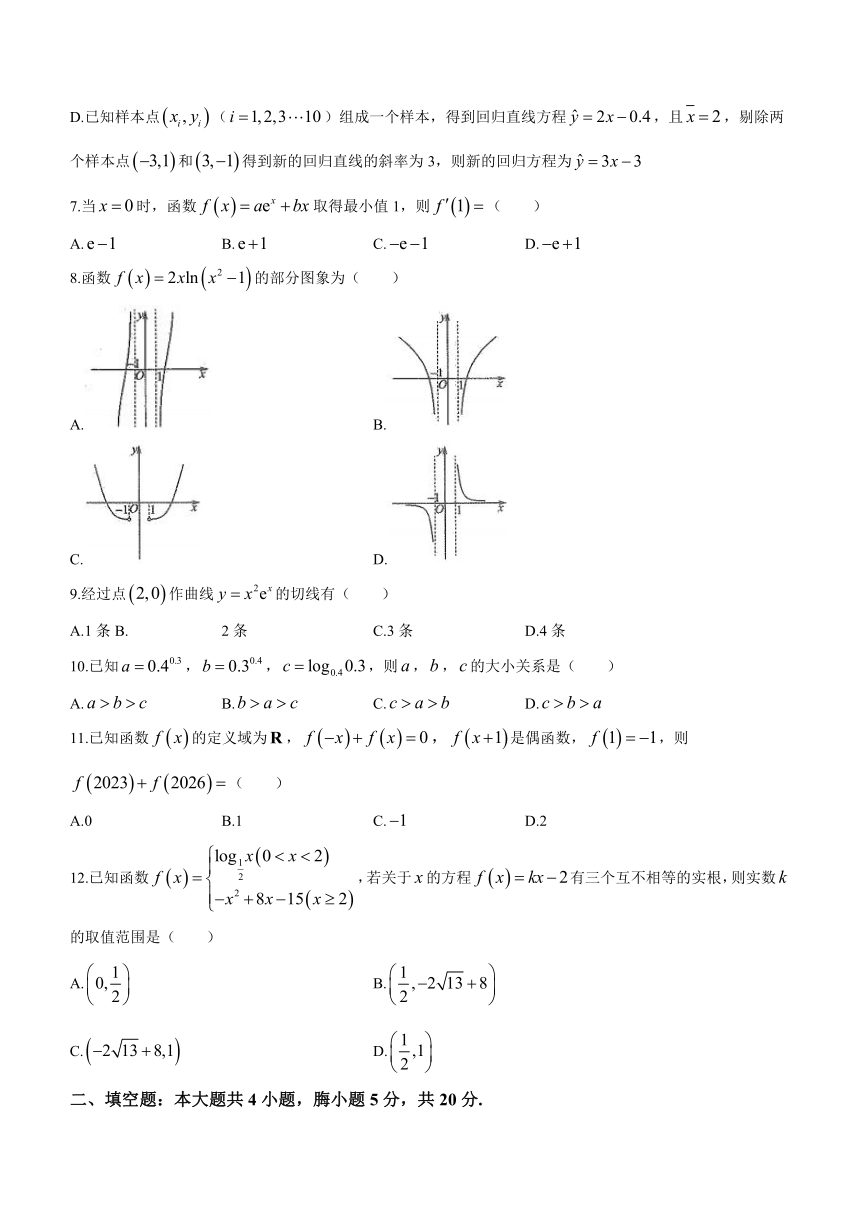
8.函数的部分图象为( )
A. B.
C. D.
9.经过点作曲线的切线有( )
A.1条B. 2条 C.3条 D.4条
10.已知,,,则,,的大小关系是( )
A. B. C. D.
11.已知函数的定义域为,,是偶函数,,则( )
A.0 B.1 C. D.2
12.已知函数,若关于的方程有三个互不相等的实根,则实数的取值范围是( )
A. B.
C. D.
二、填空题:本大题共4小题,脢小题5分,共20分.
13.若,则______.
14.若函数为奇函数,则实数的值为______.
15.设是定义在上的奇函数,当时,有恒成立,则不等式的解集是______.
16.已知函数,若函数在区间上存在最大值,则实数的取值范围是______.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)计算:
(1);
(2).
18.(本小题满分12分)春节联欢晩会是我国在除夕晩上举办的大型欢庆晩会,全国家家户户围坐在电视机前欣赏一年中最重要的晩会,下表为某年观看春晩的人数百分比:
假设统计人数为200人,下表为分析年龄大于30的人和年龄不大于30的人对春晩是否满意的列联表:
(1)请将列联表补充完整;
满意 不满意 合计
年龄不大于30 50
年龄大于30 66
合计
年龄(岁) 百分比
10%
27%
17%
13%
33%
(2)能否有99%的把握认为年龄大于30的人和年龄不大于30的人对春晩评价有差异.
附:,其中.
0.050 0.010 0.001
3.841 6.635 10.828
19.(本小题满分12分)已知函数().
(1)当时,求函数的极值;
(2)若函数在区间上单调递增,求实数的取值范围.
20.(本小题满分12分)已知,:“函数的定义域为”,:“,使得成立”.
(1)若为真命题,求实数的取值范围;
(2)若“”为真命题,“”为假命题,求实数的取值范围.
21.(本小题满分12分)“城市公交”泛指城市范围内定线运营的公共汽车及轨道交通等交通方式,也是人们日常出行的主要方式.某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间与乘客等候人数之间的关系,经过调查得到如下数据:
间隔时间(分钟) 6 8 10 12 14
等候人数(人) 15 18 20 24 23
(1)根据以上数据作出折线图,易知可用线性回归模型拟合与的关系,请用相关系数加以说明;
(2)建立关于的回归直线方程,并预测车辆发车间隔时间为20分钟时乘客的等候人数.附:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为,;
相关系数;.
22.(本小题满分12分)已知函数.
(1)当时,求函数的图像在点处的切线方程;
(2)讨论函数的单调性;
(3)若恒成立,求实数的取值范围.
雅安市2022-2023学年高二下学期期末检测
数学试卷
(文科)答案及评分标准
选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D C D B D A A C C B B
二、填空题
13.- 2 14.1 15. 16.
三、解答题
17.【答案】解:
(1)
= …………………………………………2分
= …………………………………………4分
= …………………………………………5分
(2)
= …………………………7分
= ………………………………………9分
= …………………………………………10分
18.【详解】(1)年龄不大于30的人有人,则年龄不大于30对春晩不满意的人有人;年龄大于30的人,则年龄大于30对春晩满意的人有人,所以,列联表如下:
满意 不满意 合计
年龄不大于30 50 24 74
年龄大于30 60 66 126
合计 110 90 200
…………………………………………6分
(2) …………………………………………8分
………………………………………………10分
故有的把握认为年龄大于30的人和年龄不大于30的人对春晩评价有差异.………12分
19.【详解】(1)函数的定义域为, ……………………………………1分
当时, 求导得, ………………………3分
整理得:. ………………………………………………………4分
由得;由得
从而,函数减区间为,增区间为 …………………………………5分
所以函数极小值为,无极大值. …………………………………6分
(2)由已知时,恒成立,即恒成立, …………8分
即恒成立,则. ………………………………………………10分
令函数,由知在单调递增,
从而. ………………………………………………………………11分
经检验知,当时,函数不是常函数,所以a的取值范围是. ………12分
20.【详解】(1)当为真命题时,在上有解, …………………2分
所以, ……………………………………………………………………4分
当时取,有最大值3,所以,
所以实数m的取值范围为; ………………………………………………………6分
(2)当为真命题时,当时,,定义域为,满足题意; …………7分
当时,要使的定义域为R,则,
解得, …………………………………………………………………………9分
综上可知:的取值范围是.因为为真命题且为假命题,
所以一真一假, ……………………………………………………………………10分
当真假时,,解得,当假真时,,此时,
综上,的取值范围是. ……………………………………………12分
21.【详解】(1)由题意,知,,………………………………………2分
,,…………4分
所以.又,则.
因为与的相关系数近似为0.95,说明与的线性相关非常高,
所以可以用线性回归模型拟合与的关系.…………………………………………6分
由(1)可得,,
则,………………………………………………………8分
所以关于的回归直线方程为,………………………………………10分
当时,,
所以预测车辆发车间隔时间为20分钟时乘客的等候人数为31人.…………………12分
22.【详解】(1)当时,,则. …………………1分
根据导数的几何意义,可得函数的图像在点处的切线斜率,
又.………………………………………………………………………2分
所以,切线方程为,整理可得.………………3分
(2)定义域为R,.……………………………………………………4分
当时,在R上恒成立,所以在R上单调递增;
当时,解,即,解得,……………………………………6分
解,得,则在上单调递增,
解,得,则在上单调递减.
综上所述,当时,在R上单调递增;当时,在上单调递增,在上单调递减.………………………………………………………………………7分
(3)由(2)知,当时,在R上单调递增,又,所以当时,,不满足要求,所以.…………………………………………9分
则由(2)知,在时,取得最小值.
要使恒成立,则只需满足即可,即.………10分
令,即.
.令,则.
当时,,当时,,
所以,在处取得极大值,也是最大值,所以.
又,所以,所以有.…………………………………………………11分
即当时,,有成立.
所以,实数的取值范围为.………………………………………………………………12分
(文科)数学试题
(本试卷满分150分,答题时间120分钟)
注意事项:
1.答题前,考生务必将自己的姓名、考号用0.5毫米的黑色墨迹签字笔填写在答题卡上,并检查条形码粘贴是否正确.
2.选择题使用2B铅笔填涂在答题卡对应题目标号的位置上;非选择题用0.5毫米黑色墨迹签字笔书写在答题卡的对应框内,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效.
3.考试结束后,将答题卡收回.
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求的.
1.已知,则复数在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知集合,,则( )
A. B. C. D.
3.设函数则( )
A.1 B.2 C.4 D.8
4.函数的定义域是( )
A. B. C. D.
5.已知命题:,;命题:直线:与:相互垂直的充要条件为,则下列命题中为真命题的是( )
A. B. C. D.
6.下列说法中正确的是( )
A.“”是“”成立的充分不必要条件
B.命题:,,则,,
C.在研究成对数据的相关关系时,相关关系越强,相关系数越接近于1
D.已知样本点()组成一个样本,得到回归直线方程,且,剔除两个样本点和得到新的回归直线的斜率为3,则新的回归方程为
7.当时,函数取得最小值1,则( )
A. B. C. D.
8.函数的部分图象为( )
A. B.
C. D.
9.经过点作曲线的切线有( )
A.1条B. 2条 C.3条 D.4条
10.已知,,,则,,的大小关系是( )
A. B. C. D.
11.已知函数的定义域为,,是偶函数,,则( )
A.0 B.1 C. D.2
12.已知函数,若关于的方程有三个互不相等的实根,则实数的取值范围是( )
A. B.
C. D.
二、填空题:本大题共4小题,脢小题5分,共20分.
13.若,则______.
14.若函数为奇函数,则实数的值为______.
15.设是定义在上的奇函数,当时,有恒成立,则不等式的解集是______.
16.已知函数,若函数在区间上存在最大值,则实数的取值范围是______.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)计算:
(1);
(2).
18.(本小题满分12分)春节联欢晩会是我国在除夕晩上举办的大型欢庆晩会,全国家家户户围坐在电视机前欣赏一年中最重要的晩会,下表为某年观看春晩的人数百分比:
假设统计人数为200人,下表为分析年龄大于30的人和年龄不大于30的人对春晩是否满意的列联表:
(1)请将列联表补充完整;
满意 不满意 合计
年龄不大于30 50
年龄大于30 66
合计
年龄(岁) 百分比
10%
27%
17%
13%
33%
(2)能否有99%的把握认为年龄大于30的人和年龄不大于30的人对春晩评价有差异.
附:,其中.
0.050 0.010 0.001
3.841 6.635 10.828
19.(本小题满分12分)已知函数().
(1)当时,求函数的极值;
(2)若函数在区间上单调递增,求实数的取值范围.
20.(本小题满分12分)已知,:“函数的定义域为”,:“,使得成立”.
(1)若为真命题,求实数的取值范围;
(2)若“”为真命题,“”为假命题,求实数的取值范围.
21.(本小题满分12分)“城市公交”泛指城市范围内定线运营的公共汽车及轨道交通等交通方式,也是人们日常出行的主要方式.某城市的公交公司为了方便市民出行,科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为了研究车辆发车间隔时间与乘客等候人数之间的关系,经过调查得到如下数据:
间隔时间(分钟) 6 8 10 12 14
等候人数(人) 15 18 20 24 23
(1)根据以上数据作出折线图,易知可用线性回归模型拟合与的关系,请用相关系数加以说明;
(2)建立关于的回归直线方程,并预测车辆发车间隔时间为20分钟时乘客的等候人数.附:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为,;
相关系数;.
22.(本小题满分12分)已知函数.
(1)当时,求函数的图像在点处的切线方程;
(2)讨论函数的单调性;
(3)若恒成立,求实数的取值范围.
雅安市2022-2023学年高二下学期期末检测
数学试卷
(文科)答案及评分标准
选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D C D B D A A C C B B
二、填空题
13.- 2 14.1 15. 16.
三、解答题
17.【答案】解:
(1)
= …………………………………………2分
= …………………………………………4分
= …………………………………………5分
(2)
= …………………………7分
= ………………………………………9分
= …………………………………………10分
18.【详解】(1)年龄不大于30的人有人,则年龄不大于30对春晩不满意的人有人;年龄大于30的人,则年龄大于30对春晩满意的人有人,所以,列联表如下:
满意 不满意 合计
年龄不大于30 50 24 74
年龄大于30 60 66 126
合计 110 90 200
…………………………………………6分
(2) …………………………………………8分
………………………………………………10分
故有的把握认为年龄大于30的人和年龄不大于30的人对春晩评价有差异.………12分
19.【详解】(1)函数的定义域为, ……………………………………1分
当时, 求导得, ………………………3分
整理得:. ………………………………………………………4分
由得;由得
从而,函数减区间为,增区间为 …………………………………5分
所以函数极小值为,无极大值. …………………………………6分
(2)由已知时,恒成立,即恒成立, …………8分
即恒成立,则. ………………………………………………10分
令函数,由知在单调递增,
从而. ………………………………………………………………11分
经检验知,当时,函数不是常函数,所以a的取值范围是. ………12分
20.【详解】(1)当为真命题时,在上有解, …………………2分
所以, ……………………………………………………………………4分
当时取,有最大值3,所以,
所以实数m的取值范围为; ………………………………………………………6分
(2)当为真命题时,当时,,定义域为,满足题意; …………7分
当时,要使的定义域为R,则,
解得, …………………………………………………………………………9分
综上可知:的取值范围是.因为为真命题且为假命题,
所以一真一假, ……………………………………………………………………10分
当真假时,,解得,当假真时,,此时,
综上,的取值范围是. ……………………………………………12分
21.【详解】(1)由题意,知,,………………………………………2分
,,…………4分
所以.又,则.
因为与的相关系数近似为0.95,说明与的线性相关非常高,
所以可以用线性回归模型拟合与的关系.…………………………………………6分
由(1)可得,,
则,………………………………………………………8分
所以关于的回归直线方程为,………………………………………10分
当时,,
所以预测车辆发车间隔时间为20分钟时乘客的等候人数为31人.…………………12分
22.【详解】(1)当时,,则. …………………1分
根据导数的几何意义,可得函数的图像在点处的切线斜率,
又.………………………………………………………………………2分
所以,切线方程为,整理可得.………………3分
(2)定义域为R,.……………………………………………………4分
当时,在R上恒成立,所以在R上单调递增;
当时,解,即,解得,……………………………………6分
解,得,则在上单调递增,
解,得,则在上单调递减.
综上所述,当时,在R上单调递增;当时,在上单调递增,在上单调递减.………………………………………………………………………7分
(3)由(2)知,当时,在R上单调递增,又,所以当时,,不满足要求,所以.…………………………………………9分
则由(2)知,在时,取得最小值.
要使恒成立,则只需满足即可,即.………10分
令,即.
.令,则.
当时,,当时,,
所以,在处取得极大值,也是最大值,所以.
又,所以,所以有.…………………………………………………11分
即当时,,有成立.
所以,实数的取值范围为.………………………………………………………………12分
同课章节目录
