三角形的边[下学期]
图片预览






文档简介
课件31张PPT。第七章 三角形香港中银大厦7.1.1三角形的边
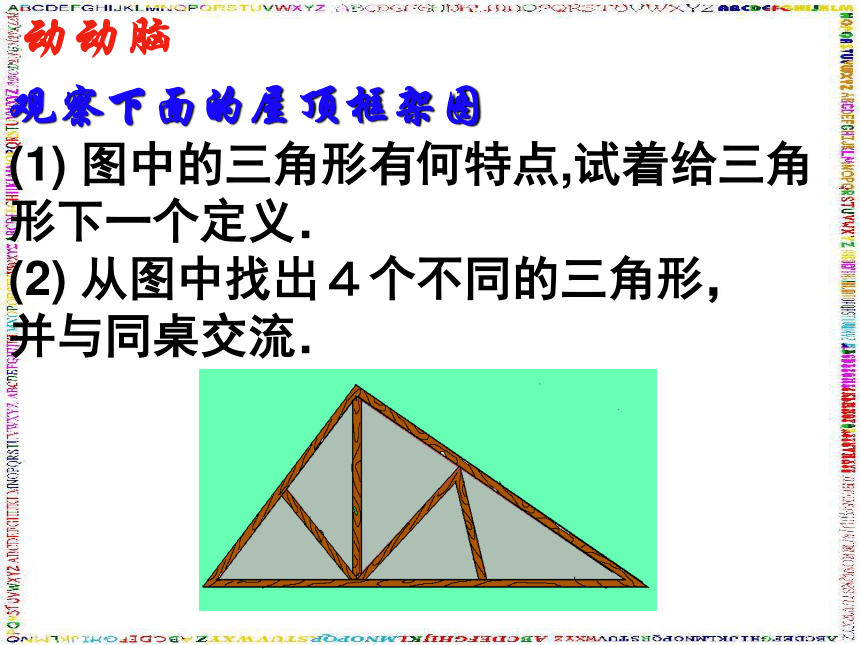
·埃及金字塔你能用手头的工具摆一个三角形吗?动动手E动动脑:观察下面的屋顶框架图 (1)?图中的三角形有何特点,试着给三角
形下一个定义. (2)?从图中找出4个不同的三角形,
并与同桌交流.想办法 为了交流的方便,需要寻找一种方法来表示三角形,那么该怎样表示三角形呢?类比线段、直线、角的表示方法,想办法并与同桌交流。
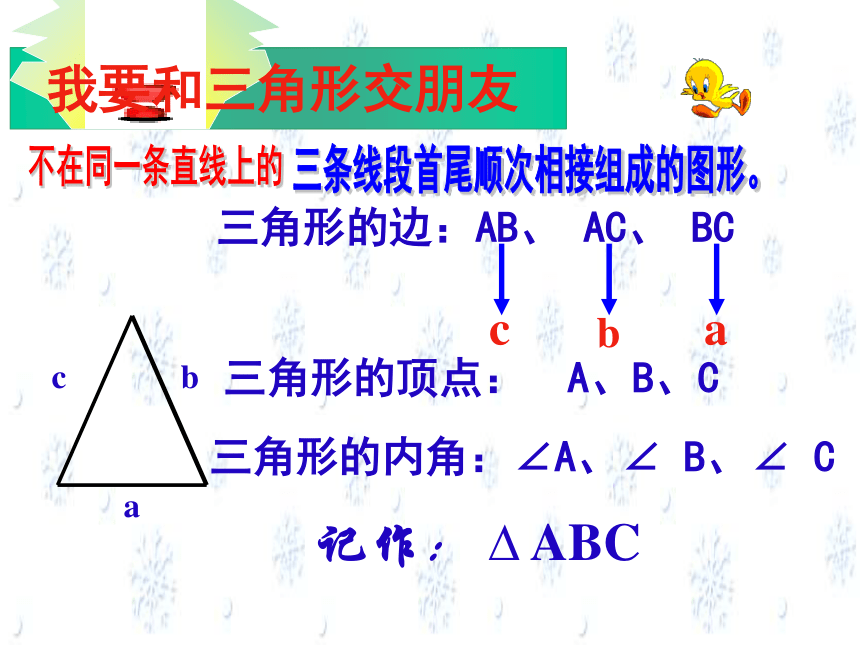
ABCabc记作: ? ABC三角形的顶点: A、B、C三角形的边:AB、 AC、 BC三角形的内角:∠A、∠ B、∠ Ccba不在同一条直线上的三条线段首尾顺次相接组成的图形。我要和三角形交朋友ABCabc不在同一条直线上的三条线段首尾顺次相接组成的图形。我要和三角形交朋友回想一下,三角形按边可以分成几类?按角呢?回答下列问题:
1.由不在同一直线上的 条线段
顺次相接所组成的图形叫做 .2. 三角形有 条边, 个内角
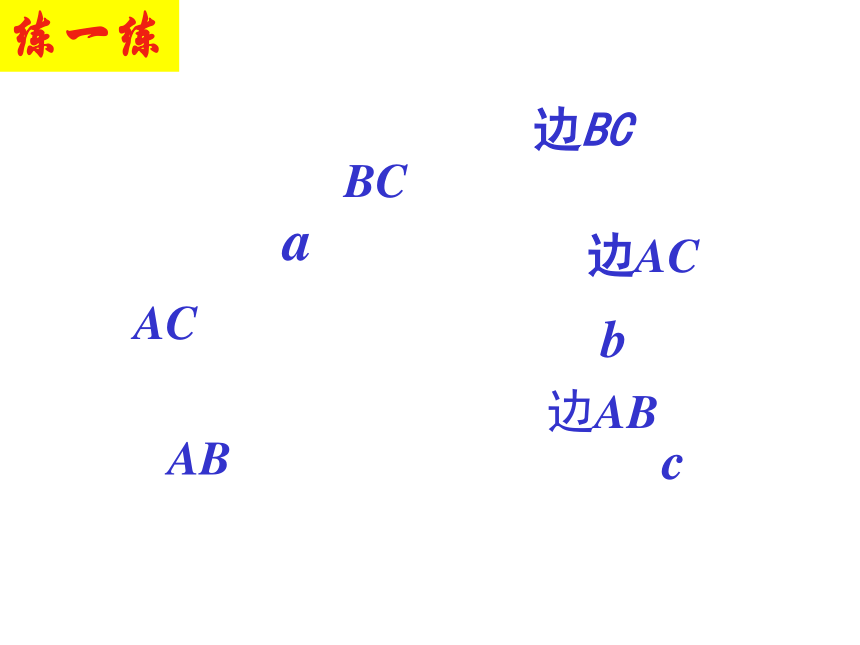
个顶点.3. “三角形” 用“ ”表示,如图三角形ABC记作“ ”.三首尾三角形三三三△△ABC练一练4. 顶点 A 所对的边是 ,用边“ ”表示,或用“ ” 表示;顶点 B 所对的边是 ,用边
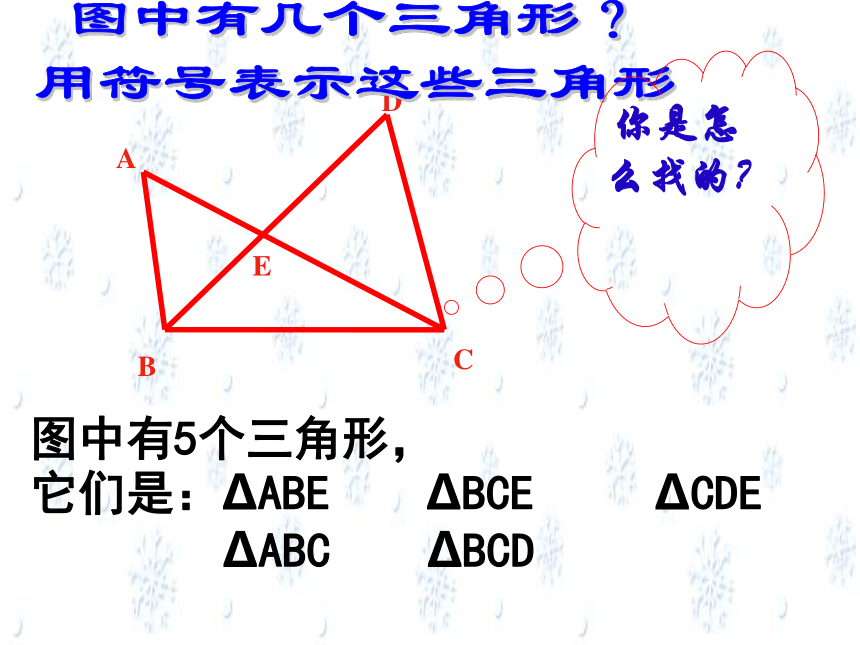
“ ”表示,或用 “ ”表示;顶点 C 所对的边是 ,用边“ ”表示,或用“ ”表示。边BCBC边AC边ABACABabc练一练ABEDC图中有几个三角形?
用符号表示这些三角形你是怎么找的?图中有5个三角形,
它们是:?ABE ?BCE ?CDE
?ABC ?BCD举出一些生活中你身边应用三角形的实际例子
生活中的三角形! 每组共有四根电线,2cm、4cm、7cm、11cm、试着用三根摆一个三角形,看能否成功。 实践质疑乐园 1是不是有三条线段就可以组成一个三角形呢?说说那次试验是失败的? 争鸣乐园 谈谈你的想法一、请看下面问题:
在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线?如果小狗在C点呢?BCACAB 争鸣乐园 谈谈你的想法在一个三角形中,任意两边之和与第三边的长度有怎样的关系呢?三角形任意两边之和大于第三边BCACAB 计算三角形的任意两边之差,并与第三边比较,你能得到什么结论?分别量出下面三个三角形的三边长度,并填入空格内。三角形的任意两边之差,小于第三边 实践质疑乐园 2 (动动手,动动脑,你能行)ACB1、a=4 b=3 c=6 能构成三角形吗?2、a=1 b=2 C=8 能构成三角形吗?谈谈你怎样验证的?根据任意两边之和大于第三边,任意两边之差小于第三边。议一议这就是我们的研究成果,你能应用于实践吗?探究乐园:请合作交流一、能否构成三角形
1.下列长度的三条线段,能构成三角形的是 ( )
A、1cm,2cm,3 cm
B、2cm,3cm ,4cm
C、6cm,8cm ,15cm
D、12cm,3cm,8cmB 尝试乐园希望你能尝试到成功的快乐用两根长度分别为4㎝和7㎝的两根木棒,
(1)用长度为2 ㎝的木棒能与它们组成三角形吗?为什么?
(2)用长度为11㎝的木棒呢?
(3)如果第三边是正整数,那么第三边可能是哪几个数?你是最棒的!第三边可能是4,5,6,7,8,9,102 尝试乐园希望你能尝试到成功的快乐2二、能构成几个三角形3.以长为以长为3㎝,5㎝,7㎝,10㎝的四条线段中的三条为边,可以构成三角形的个数是( )
( A )1个 ( B ) 2个
( C ) 3个 ( D )4个B三、三角形的周长可能是多少1.在三角形ABC中,AB=7,BC=3,并且AC为奇数,那么三角形ABC的周长__ _。15或17或192. 尝试乐园希望你能尝试到成功的快乐23.以长为2.2.一个三角形有两条边相等三角形的一边长3㎝,另一边长5㎝,那么该三角形的周长是( )
A.8 B.11
C.13 D.11或13D 3.在三角形ABC中,三边均为整数,周长为11,且有一边为4,则这个三角形可能的最长边是( )
A )7 ( B ) 6
( C ) 5 ( D ) 4 尝试乐园希望你能尝试到成功的快乐2C四、如何化简代数式若三角形ABC的三边长为a ,b , c,试化简
|a-b-c|+|b-c-a|+|c-a-b|2.解:根据三角形三边关系知:
b+c>a, a+c>b, a+b>c
所以原式=b+c-a+a+c-b+a+b-c
=a+b+c回顾与反思1.你会数三角形吗?下列各图中各有几个三角形?( )( )( 10 )( ? )数完后请说出你发现的规律。小课题研究你是数学小天才!ABDCBACDE36人行横道请用所学的数学知识解释:为什么经常有行人斜穿马路而不走人行横道或者2两点之间的所有连线中,线段最短1三角形任意两边之和大于第三边.A.B2.如图,有A、B、C、D四个村庄,打算公用一个水厂,若要使用的水管最节约,水厂应过村庄的什么地方?学习了本节课你有哪些收获?再见再见探究方向1、通过身边的实例认识三角形。
2、通过实例的探究掌握三角形三边关系。
3、积极参加交流,能通过观察、猜想、实践、推理进行探究和创新,敢于表达自己的见解。
·埃及金字塔你能用手头的工具摆一个三角形吗?动动手E动动脑:观察下面的屋顶框架图 (1)?图中的三角形有何特点,试着给三角
形下一个定义. (2)?从图中找出4个不同的三角形,
并与同桌交流.想办法 为了交流的方便,需要寻找一种方法来表示三角形,那么该怎样表示三角形呢?类比线段、直线、角的表示方法,想办法并与同桌交流。
ABCabc记作: ? ABC三角形的顶点: A、B、C三角形的边:AB、 AC、 BC三角形的内角:∠A、∠ B、∠ Ccba不在同一条直线上的三条线段首尾顺次相接组成的图形。我要和三角形交朋友ABCabc不在同一条直线上的三条线段首尾顺次相接组成的图形。我要和三角形交朋友回想一下,三角形按边可以分成几类?按角呢?回答下列问题:
1.由不在同一直线上的 条线段
顺次相接所组成的图形叫做 .2. 三角形有 条边, 个内角
个顶点.3. “三角形” 用“ ”表示,如图三角形ABC记作“ ”.三首尾三角形三三三△△ABC练一练4. 顶点 A 所对的边是 ,用边“ ”表示,或用“ ” 表示;顶点 B 所对的边是 ,用边
“ ”表示,或用 “ ”表示;顶点 C 所对的边是 ,用边“ ”表示,或用“ ”表示。边BCBC边AC边ABACABabc练一练ABEDC图中有几个三角形?
用符号表示这些三角形你是怎么找的?图中有5个三角形,
它们是:?ABE ?BCE ?CDE
?ABC ?BCD举出一些生活中你身边应用三角形的实际例子
生活中的三角形! 每组共有四根电线,2cm、4cm、7cm、11cm、试着用三根摆一个三角形,看能否成功。 实践质疑乐园 1是不是有三条线段就可以组成一个三角形呢?说说那次试验是失败的? 争鸣乐园 谈谈你的想法一、请看下面问题:
在A点的小狗,为了尽快吃到B点的香肠,它会选择哪条路线?如果小狗在C点呢?BCACAB 争鸣乐园 谈谈你的想法在一个三角形中,任意两边之和与第三边的长度有怎样的关系呢?三角形任意两边之和大于第三边BCACAB 计算三角形的任意两边之差,并与第三边比较,你能得到什么结论?分别量出下面三个三角形的三边长度,并填入空格内。三角形的任意两边之差,小于第三边 实践质疑乐园 2 (动动手,动动脑,你能行)ACB1、a=4 b=3 c=6 能构成三角形吗?2、a=1 b=2 C=8 能构成三角形吗?谈谈你怎样验证的?根据任意两边之和大于第三边,任意两边之差小于第三边。议一议这就是我们的研究成果,你能应用于实践吗?探究乐园:请合作交流一、能否构成三角形
1.下列长度的三条线段,能构成三角形的是 ( )
A、1cm,2cm,3 cm
B、2cm,3cm ,4cm
C、6cm,8cm ,15cm
D、12cm,3cm,8cmB 尝试乐园希望你能尝试到成功的快乐用两根长度分别为4㎝和7㎝的两根木棒,
(1)用长度为2 ㎝的木棒能与它们组成三角形吗?为什么?
(2)用长度为11㎝的木棒呢?
(3)如果第三边是正整数,那么第三边可能是哪几个数?你是最棒的!第三边可能是4,5,6,7,8,9,102 尝试乐园希望你能尝试到成功的快乐2二、能构成几个三角形3.以长为以长为3㎝,5㎝,7㎝,10㎝的四条线段中的三条为边,可以构成三角形的个数是( )
( A )1个 ( B ) 2个
( C ) 3个 ( D )4个B三、三角形的周长可能是多少1.在三角形ABC中,AB=7,BC=3,并且AC为奇数,那么三角形ABC的周长__ _。15或17或192. 尝试乐园希望你能尝试到成功的快乐23.以长为2.2.一个三角形有两条边相等三角形的一边长3㎝,另一边长5㎝,那么该三角形的周长是( )
A.8 B.11
C.13 D.11或13D 3.在三角形ABC中,三边均为整数,周长为11,且有一边为4,则这个三角形可能的最长边是( )
A )7 ( B ) 6
( C ) 5 ( D ) 4 尝试乐园希望你能尝试到成功的快乐2C四、如何化简代数式若三角形ABC的三边长为a ,b , c,试化简
|a-b-c|+|b-c-a|+|c-a-b|2.解:根据三角形三边关系知:
b+c>a, a+c>b, a+b>c
所以原式=b+c-a+a+c-b+a+b-c
=a+b+c回顾与反思1.你会数三角形吗?下列各图中各有几个三角形?( )( )( 10 )( ? )数完后请说出你发现的规律。小课题研究你是数学小天才!ABDCBACDE36人行横道请用所学的数学知识解释:为什么经常有行人斜穿马路而不走人行横道或者2两点之间的所有连线中,线段最短1三角形任意两边之和大于第三边.A.B2.如图,有A、B、C、D四个村庄,打算公用一个水厂,若要使用的水管最节约,水厂应过村庄的什么地方?学习了本节课你有哪些收获?再见再见探究方向1、通过身边的实例认识三角形。
2、通过实例的探究掌握三角形三边关系。
3、积极参加交流,能通过观察、猜想、实践、推理进行探究和创新,敢于表达自己的见解。
