数学人教A版(2019)选择性必修第一册1.4.2用空间向量研究距离、夹角问题 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.4.2用空间向量研究距离、夹角问题 课件(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 475.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
1.4.1
用空间向量研究距离、夹角问题(第1课时)
人教A版(2019)选择性必修第一册
学习目标
1.能用向量表示点到直线、点到平面、互相平行的直线、互相平行的平面的距离。
2.能用向量方法解决立体几何中相关的距离问题。
3.核心素养:逻辑推理、直观想象、数学运算
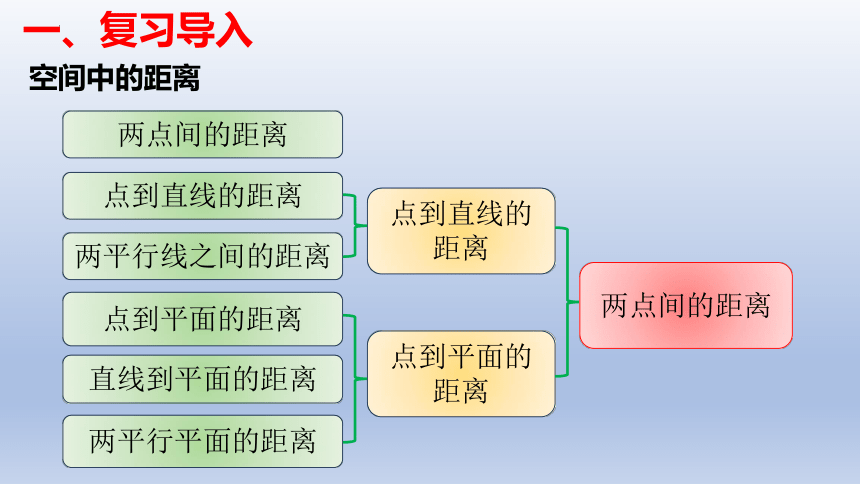
一、复习导入
空间中的距离
两点间的距离
点到直线的距离
两平行线之间的距离
点到平面的距离
直线到平面的距离
两平行平面的距离
点到直线的距离
点到平面的距离
两点间的距离
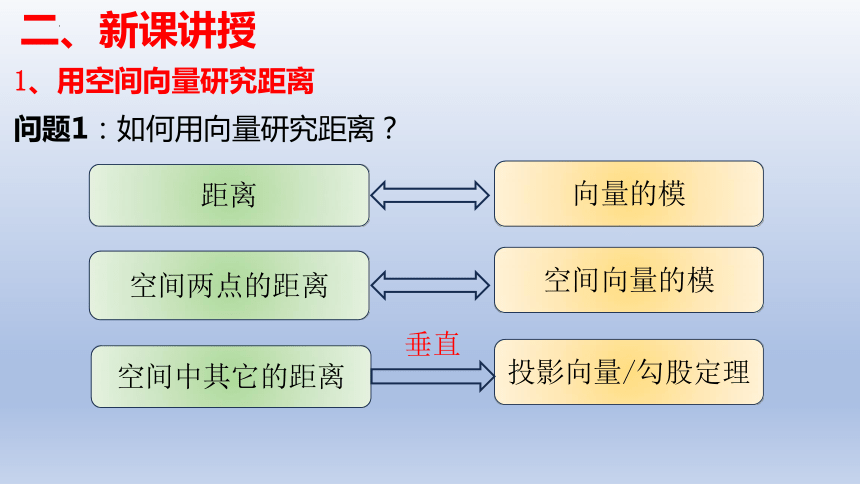
二、新课讲授
1、用空间向量研究距离
问题1:如何用向量研究距离?
距离
空间两点的距离
空间中其它的距离
向量的模
空间向量的模
投影向量/勾股定理
垂直
P
问题2:如何用向量法求点到直线的距离?
Q
A
设是直线的单位方向向量,A是直线上的点
分析:①求出||;
②求出到上的投影向量||;
③应用勾股定理求出PQ的长度。
设= 则向量在直线上的投影向量= (
所以= (
则|= |
所以==
P
Q
A
设是直线的方向向量,A是直线上的定点
分析:先求出的单位方向向量
设= 则向量在直线上的投影向量= (
则|= | = | =
所以==
直线上的单位方向向量:
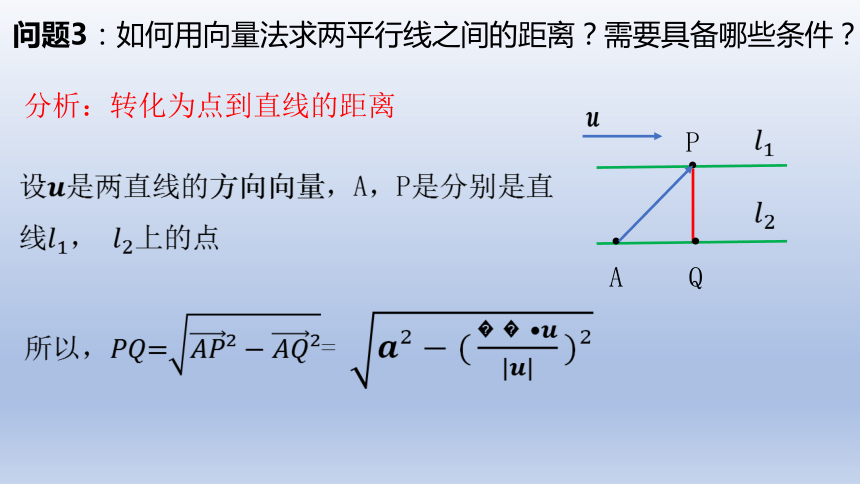
问题3:如何用向量法求两平行线之间的距离?需要具备哪些条件?
P
Q
A
分析:转化为点到直线的距离
设是两直线的方向向量,A,P是分别是直线, 上的点
所以==
问题3:如何用向量法求空间中点到平面的距离?
P
Q
A
设是平面α的法向量,A是平面α内的点
分析:转化为点到直线的距离
投影向量= (;
|= | = | =
所以,点P到平面α的距离为:
根据定义,过点P作PQ⊥α,垂足为Q,垂线段PQ的长度为点P到平面α的距离
距离问题 图示 向量法距离公式
两点间的距离
点到直线的距离
两平行线之间的距离
点到平面的距离
=| |
==
==
|= | =
三、巩固新知
例6 如图,在棱长为1的正方体ABCD-A B C D 中,E为线段A B 的中点,F为线段AB的中点.
(1)求点B到直线AC 的距离;
(2)求直线FC到平面平面AEC 的距离
解:(1)以D 为原点,以D A , D C , D D所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
则A(1,0,1),B(1, , ),C(0,1,1),
C (0,1,0),E(0, , ),F(1, ,1)
所以=(0, , ), = (-1, 1, )
直线AC 的单位方向向量= = (-1,1,-1)
设= = (0,1,0)
则 = ,
=,
所以点B到直线AC 的距离为:
==
解:(2)因为= =(-1, ,0),所以FC∥ .
因为 平面AEC , 平面AEC .
所以FC∥平面AEC .
所以点F到平面平面AEC 的距离即为直线FC到平面平面AEC 的距离.
设=(x,y,z)是平面AEC 的法向量,则
所以
取z=1,则x=1,y,2
所以=(1,2,1)是平面AEC 的一个法向量
有因为= (0, ,0),
所以点F到平面AEC 的距离为:
= ||=
小结:用向量法解决距离的“三步曲”
1、将几何问题转化为向量问题:建立空间直角坐标系
2、进行向量运算:公式
3、回到图形问题:得到所求距离
四、课堂小结
1.空间中的距离问题.
2. 投影向量、勾股定理、向量数量积运算相结合.
3.距离的向量计算公式.
五、作业布置
课本P35:练习 第3题
1.4.1
用空间向量研究距离、夹角问题(第1课时)
人教A版(2019)选择性必修第一册
学习目标
1.能用向量表示点到直线、点到平面、互相平行的直线、互相平行的平面的距离。
2.能用向量方法解决立体几何中相关的距离问题。
3.核心素养:逻辑推理、直观想象、数学运算
一、复习导入
空间中的距离
两点间的距离
点到直线的距离
两平行线之间的距离
点到平面的距离
直线到平面的距离
两平行平面的距离
点到直线的距离
点到平面的距离
两点间的距离
二、新课讲授
1、用空间向量研究距离
问题1:如何用向量研究距离?
距离
空间两点的距离
空间中其它的距离
向量的模
空间向量的模
投影向量/勾股定理
垂直
P
问题2:如何用向量法求点到直线的距离?
Q
A
设是直线的单位方向向量,A是直线上的点
分析:①求出||;
②求出到上的投影向量||;
③应用勾股定理求出PQ的长度。
设= 则向量在直线上的投影向量= (
所以= (
则|= |
所以==
P
Q
A
设是直线的方向向量,A是直线上的定点
分析:先求出的单位方向向量
设= 则向量在直线上的投影向量= (
则|= | = | =
所以==
直线上的单位方向向量:
问题3:如何用向量法求两平行线之间的距离?需要具备哪些条件?
P
Q
A
分析:转化为点到直线的距离
设是两直线的方向向量,A,P是分别是直线, 上的点
所以==
问题3:如何用向量法求空间中点到平面的距离?
P
Q
A
设是平面α的法向量,A是平面α内的点
分析:转化为点到直线的距离
投影向量= (;
|= | = | =
所以,点P到平面α的距离为:
根据定义,过点P作PQ⊥α,垂足为Q,垂线段PQ的长度为点P到平面α的距离
距离问题 图示 向量法距离公式
两点间的距离
点到直线的距离
两平行线之间的距离
点到平面的距离
=| |
==
==
|= | =
三、巩固新知
例6 如图,在棱长为1的正方体ABCD-A B C D 中,E为线段A B 的中点,F为线段AB的中点.
(1)求点B到直线AC 的距离;
(2)求直线FC到平面平面AEC 的距离
解:(1)以D 为原点,以D A , D C , D D所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系.
则A(1,0,1),B(1, , ),C(0,1,1),
C (0,1,0),E(0, , ),F(1, ,1)
所以=(0, , ), = (-1, 1, )
直线AC 的单位方向向量= = (-1,1,-1)
设= = (0,1,0)
则 = ,
=,
所以点B到直线AC 的距离为:
==
解:(2)因为= =(-1, ,0),所以FC∥ .
因为 平面AEC , 平面AEC .
所以FC∥平面AEC .
所以点F到平面平面AEC 的距离即为直线FC到平面平面AEC 的距离.
设=(x,y,z)是平面AEC 的法向量,则
所以
取z=1,则x=1,y,2
所以=(1,2,1)是平面AEC 的一个法向量
有因为= (0, ,0),
所以点F到平面AEC 的距离为:
= ||=
小结:用向量法解决距离的“三步曲”
1、将几何问题转化为向量问题:建立空间直角坐标系
2、进行向量运算:公式
3、回到图形问题:得到所求距离
四、课堂小结
1.空间中的距离问题.
2. 投影向量、勾股定理、向量数量积运算相结合.
3.距离的向量计算公式.
五、作业布置
课本P35:练习 第3题
