北师大版 八年级上册 数学4.1函数 教案
文档属性
| 名称 | 北师大版 八年级上册 数学4.1函数 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 920.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览


文档简介
第四章 一次函数
4.1 函数
一、教学目标
1.经历从具体实例中抽象出函数概念的过程,进一步感悟抽象的数学思想,积累抽象概括的活动经验.
2.初步理解函数的概念,能判断两个变量间的关系是不是函数关系,初步形成利用函数的观点认识现实世界的意识.
二、教学重点及难点
重点:
1.掌握函数概念.
2.判断两个变量之间的关系是否可看做函数.
3.能把实际问题抽象概括为函数问题.
难点:
1.理解函数的概念.
2.能把实际问题抽象概括为函数问题.
三、教学用具
多媒体课件.
四、相关资源
《摩天轮》动画,《摩天轮旋转时间与摩天轮上一点高度的关系图像》图片.
五、教学过程
【探究新知】
一、情景导入,引起兴趣
活动1 欣赏美丽的函数图象
活动2 尝试解决故事中的数学问题
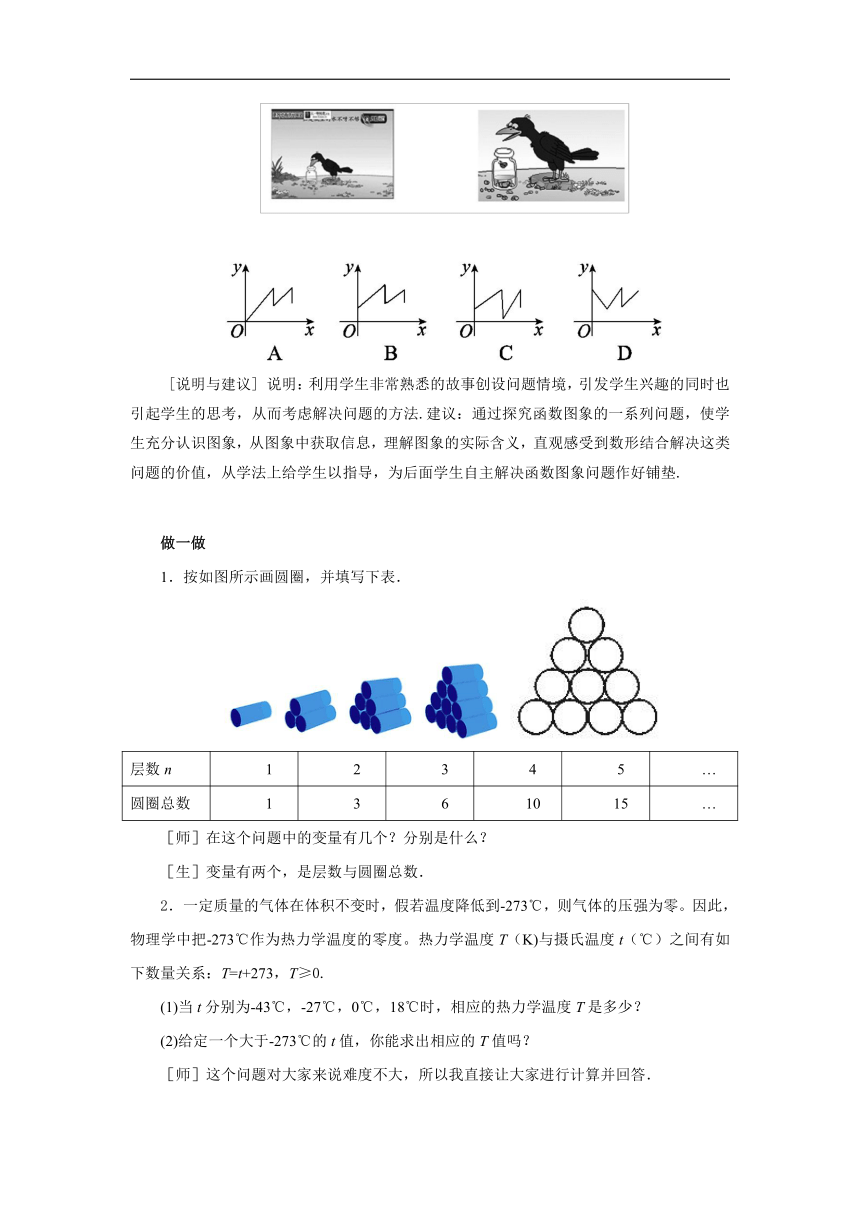
你一定知道乌鸦喝水的故事吧!一个紧口瓶中盛有一些水,乌鸦想喝水,但是嘴够不着瓶中的水,于是乌鸦衔来一些小石子放入瓶中,瓶中水面的高度随石子的增多而上升,乌鸦喝到了水.但是还没解渴,瓶中水面就下降到乌鸦够不着的高度了,乌鸦只好再去衔些石子放入瓶中,水面又上升,乌鸦终于喝足了水,哇哇地飞走了.如果设衔入瓶中石子的体积为x,瓶中水面的高度为y,下面能大致表示上面故事情节的图象是( B )
[说明与建议] 说明:利用学生非常熟悉的故事创设问题情境,引发学生兴趣的同时也引起学生的思考,从而考虑解决问题的方法.建议:通过探究函数图象的一系列问题,使学生充分认识图象,从图象中获取信息,理解图象的实际含义,直观感受到数形结合解决这类问题的价值,从学法上给学生以指导,为后面学生自主解决函数图象问题作好铺垫.
做一做
1.按如图所示画圆圈,并填写下表.
层数n 1 2 3 4 5 …
圆圈总数 1 3 6 10 15 …
[师]在这个问题中的变量有几个?分别是什么?
[生]变量有两个,是层数与圆圈总数.
一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零。因此,物理学中把-273℃作为热力学温度的零度。热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别为-43℃,-27℃,0℃,18℃时,相应的热力学温度T是多少?
(2)给定一个大于-273℃的t值,你能求出相应的T值吗?
[师]这个问题对大家来说难度不大,所以我直接让大家进行计算并回答.
[生](1)当t=-43℃时,T=-43+273=220 K
当t=-27℃时,T=-27+273=246 K
当t=0℃时,T=0+273=273 K
当t=18℃时,T=18+273=291 K
能求出相应的T值.
设计意图:通过几个现实生活中的函数原型,让学生感受函数表示方式的多样性,以图像、表格、表达式三种形式呈现几个与生活相关的情境,并最终总结出函数的三种表示方法,从而使学生对函数有一个更为准确、全面的认识。选用做一做2的目的,一是提供以表达式表示的函数,有利于学生对函数形成全面的认识;二是该问题有一个特点,自变量的取值不仅可以是正数,也可以是零或负数,从而使学生对自变量的取值范围有更全面的认识。
议一议
[师]在上面我们共研究了三个问题,下面大家探讨一下,在这三个问题中的共同点是什么?相异点又是什么呢?
[生]相同点是:这三个问题中都研究了两个变量.
不同点是:在第一个问题中,是以图象的形式表示两个变量之间的关系;第二个问题中是以表格的形式表示两个变量间的关系;第三个问题是以代数表达式来表示两个变量间的关系的.
[师]非常棒,可见大家是经过了一番研究的,而且大家的研究水平已有很大提高,在学习的过程中就应该以这种探索的精神去解决问题,不仅能把知识学深、学透,更重要的是培养了大家解决问题的能力.这位同学基本上总结的是全面的.
上面分别以图象、表格、代数表达式三种形式呈现了生活化的场景,通过对这三个问题的研究,让大家明确“给定其中某一个变量的值,相应地就确定了另一个变量的值”这一共性.
函数的概念
在上面各例中,都有两个变量,给定其中某一个变量(自变量)的值,相应地就确定了另一个变量(因变量)的值.
一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y 是x的函数,其中x是自变量,y是因变量.
表示函数的方法一般有:列表法、关系式法(也称为解析式、表达式)和图象法。
想一想:上述问题中,自变量能取哪些值?
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值。
【典例精讲】
已知菱形ABCD的对角线AC长为4,BD的长x在变化,则菱形的面积为多少?
解:y=×4x,即y=2x.
本题中有几个变量,能把其中某个变量看成另一个变量的函数吗?
有两个变量,即BD的长x,菱形的面积y,y是x的函数.
【课堂练习】
1.下列各题中分别有几个变量?你能将其中某个变量看成另一个变量的函数吗?
① ②
图1 图2
③
通话时间t/分 0<t≤3 3<t≤4 4<t≤5 5<t≤6 6<t≤7 …
话费y/元 0.4 0.8 1.2 1.6 2.0 …
2.下列各题中,哪些是函数关系,哪些不是函数关系:
(1)在一定的时间内,匀速运动所走的路程和速度.
(2)在平静的湖面上,投入一粒石子,泛起的波纹的周长与半径.
(3)x+3与x.
(4)三角形的面积一定,它的一边和这边上的高.
(5)正方形的面积和梯形的面积.
(6)水管中水流的速度和水管的长度.
(7)圆的面积和它的周长.
(8)底是定长的等腰三角形的周长与底边上的高.
3.下列变化过程得出的函数关系式是否正确,如果错误,请指出正确的结果;如果正确,指出式子中的自变量和因变量.
(1)设一长方体盒子高为10 cm,底面是正方形,这个长方体的体积V(cm3)与底面边长a(cm)的关系式为V=10a2;
(2)某市出租车起步价是7元(路程小于或等于2千米),超过2千米每增加1千米加收1.6元,出租车车费y(元)与行程x(千米)之间的函数关系式为y=1.6(x-2)+7(x≥2);
(3)计划花500元购买篮球,所能购买的总数n(个)与单价a(元)的关系为n=;
(4)用总长为60 m的篱笆围成矩形场地,矩形面积S(m2)与一边长l(m)之间的关系式为S=l(60-l).
4.图3是弹簧挂上重物后,弹簧的长度y(厘米)与所挂物体的质量x(千克)之间的变化关系图.根据图象,回答问题:
图3
(1)不挂重物时,弹簧长多少厘米?
(2)当所挂物体的质量分别为5千克,10千克,15千克,20千克时弹簧的长度分别是多少厘米?
(3)当物体的质量x取0千克至20千克之间任一确定的值时,相应的弹簧的长度y能确定吗?反过来,弹簧的长度y是15~25之间一个确定的值,你能确定所挂重物的质量是多少吗?
(4)弹簧长度y可以看成是物体质量x的函数吗?
5 求下列函数的自变量x的取值范围.
(1);
(2)y=x-1;
(3);
(4)
6.如图,这是某地区一天的气温随时间变化的图象,根据图象回答:在这一天中:
(1)______时气温最高,______时气温最低,最高气温是______,最低气温是______;
(2)20时的气温是______;
(3)______时的气温是6 ℃;
(4)______时间内,气温不断下降;
(5)______时间内,气温持续不变.
【答案】
1.①②③都含有两个变量,①中人均纯收入可以看成年份的函数,②中有效成分释放量是服用后的时间的函数,③中话费是通话时间的函数
2.(1)(2)(3)(4)(7)(8)是函数关系,(5)(6)不是.
3.解:(1)因为长方体的体积为长乘宽乘高,而长、宽、高分别为10、a、a.所以V=10a2正确.自变量是a,因变量是V.
(2)y=1.6(x-2)+7(x≥2)正确,其中x是自变量,y是因变量.
(3)n=正确.
其中a是自变量,n是因变量.
(4)S=l(60-l)错误.
因为60 m是矩形的周长,所以相邻两边的和为30 cm,其中一边长为l (m),则另一边长为(30-l)m,所以S=l(30-l).
4.(1)不挂重物时,弹簧长15 cm.
(2)当所挂重物的质量分别是5千克、10千克、15千克、20千克时,弹簧的长度分别为17.5 cm、20 cm、22.5 cm、25 cm
(3)当x取0~20之间任一确定值时,y都惟一确定;反之也是.
(4)y可以看成是x的函数.
5.分析:如果函数中含有偶次根式,则要求被开方数≥0.
.解:(1)的x的取值范围是:x≥1;
(2)y=x-1的x的取值范围是全体实数;
(3)的x的取值范围是:x≥1;
(4)的x的取值范围是全体实数;
6.(1)16,4,10℃,-4℃ (2)8℃ (3)10 (4)16-24 (5)12-14
设计意图:对求函数的定义域进行方法引导,偶次方根必需注意的地方.
六、课堂小结
本节课应掌握如下内容.
1.初步掌握函数概念,能判断两个变量间的关系是否可看做函数.
2.在一个函数关系式中,能识别自变量与因变量,给定自变量的值,相应地会求出函数的值.
3.函数的三种表达形式
(1)图象;
(2)表格;
(3)代数表达式.
七、板书设计
4.1函数
1.函数
2.表达形式
4.1 函数
一、教学目标
1.经历从具体实例中抽象出函数概念的过程,进一步感悟抽象的数学思想,积累抽象概括的活动经验.
2.初步理解函数的概念,能判断两个变量间的关系是不是函数关系,初步形成利用函数的观点认识现实世界的意识.
二、教学重点及难点
重点:
1.掌握函数概念.
2.判断两个变量之间的关系是否可看做函数.
3.能把实际问题抽象概括为函数问题.
难点:
1.理解函数的概念.
2.能把实际问题抽象概括为函数问题.
三、教学用具
多媒体课件.
四、相关资源
《摩天轮》动画,《摩天轮旋转时间与摩天轮上一点高度的关系图像》图片.
五、教学过程
【探究新知】
一、情景导入,引起兴趣
活动1 欣赏美丽的函数图象
活动2 尝试解决故事中的数学问题
你一定知道乌鸦喝水的故事吧!一个紧口瓶中盛有一些水,乌鸦想喝水,但是嘴够不着瓶中的水,于是乌鸦衔来一些小石子放入瓶中,瓶中水面的高度随石子的增多而上升,乌鸦喝到了水.但是还没解渴,瓶中水面就下降到乌鸦够不着的高度了,乌鸦只好再去衔些石子放入瓶中,水面又上升,乌鸦终于喝足了水,哇哇地飞走了.如果设衔入瓶中石子的体积为x,瓶中水面的高度为y,下面能大致表示上面故事情节的图象是( B )
[说明与建议] 说明:利用学生非常熟悉的故事创设问题情境,引发学生兴趣的同时也引起学生的思考,从而考虑解决问题的方法.建议:通过探究函数图象的一系列问题,使学生充分认识图象,从图象中获取信息,理解图象的实际含义,直观感受到数形结合解决这类问题的价值,从学法上给学生以指导,为后面学生自主解决函数图象问题作好铺垫.
做一做
1.按如图所示画圆圈,并填写下表.
层数n 1 2 3 4 5 …
圆圈总数 1 3 6 10 15 …
[师]在这个问题中的变量有几个?分别是什么?
[生]变量有两个,是层数与圆圈总数.
一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零。因此,物理学中把-273℃作为热力学温度的零度。热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别为-43℃,-27℃,0℃,18℃时,相应的热力学温度T是多少?
(2)给定一个大于-273℃的t值,你能求出相应的T值吗?
[师]这个问题对大家来说难度不大,所以我直接让大家进行计算并回答.
[生](1)当t=-43℃时,T=-43+273=220 K
当t=-27℃时,T=-27+273=246 K
当t=0℃时,T=0+273=273 K
当t=18℃时,T=18+273=291 K
能求出相应的T值.
设计意图:通过几个现实生活中的函数原型,让学生感受函数表示方式的多样性,以图像、表格、表达式三种形式呈现几个与生活相关的情境,并最终总结出函数的三种表示方法,从而使学生对函数有一个更为准确、全面的认识。选用做一做2的目的,一是提供以表达式表示的函数,有利于学生对函数形成全面的认识;二是该问题有一个特点,自变量的取值不仅可以是正数,也可以是零或负数,从而使学生对自变量的取值范围有更全面的认识。
议一议
[师]在上面我们共研究了三个问题,下面大家探讨一下,在这三个问题中的共同点是什么?相异点又是什么呢?
[生]相同点是:这三个问题中都研究了两个变量.
不同点是:在第一个问题中,是以图象的形式表示两个变量之间的关系;第二个问题中是以表格的形式表示两个变量间的关系;第三个问题是以代数表达式来表示两个变量间的关系的.
[师]非常棒,可见大家是经过了一番研究的,而且大家的研究水平已有很大提高,在学习的过程中就应该以这种探索的精神去解决问题,不仅能把知识学深、学透,更重要的是培养了大家解决问题的能力.这位同学基本上总结的是全面的.
上面分别以图象、表格、代数表达式三种形式呈现了生活化的场景,通过对这三个问题的研究,让大家明确“给定其中某一个变量的值,相应地就确定了另一个变量的值”这一共性.
函数的概念
在上面各例中,都有两个变量,给定其中某一个变量(自变量)的值,相应地就确定了另一个变量(因变量)的值.
一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y 是x的函数,其中x是自变量,y是因变量.
表示函数的方法一般有:列表法、关系式法(也称为解析式、表达式)和图象法。
想一想:上述问题中,自变量能取哪些值?
对于自变量在可取值范围内的一个确定的值a,函数有唯一确定的对应值,这个对应值称为当自变量等于a时的函数值。
【典例精讲】
已知菱形ABCD的对角线AC长为4,BD的长x在变化,则菱形的面积为多少?
解:y=×4x,即y=2x.
本题中有几个变量,能把其中某个变量看成另一个变量的函数吗?
有两个变量,即BD的长x,菱形的面积y,y是x的函数.
【课堂练习】
1.下列各题中分别有几个变量?你能将其中某个变量看成另一个变量的函数吗?
① ②
图1 图2
③
通话时间t/分 0<t≤3 3<t≤4 4<t≤5 5<t≤6 6<t≤7 …
话费y/元 0.4 0.8 1.2 1.6 2.0 …
2.下列各题中,哪些是函数关系,哪些不是函数关系:
(1)在一定的时间内,匀速运动所走的路程和速度.
(2)在平静的湖面上,投入一粒石子,泛起的波纹的周长与半径.
(3)x+3与x.
(4)三角形的面积一定,它的一边和这边上的高.
(5)正方形的面积和梯形的面积.
(6)水管中水流的速度和水管的长度.
(7)圆的面积和它的周长.
(8)底是定长的等腰三角形的周长与底边上的高.
3.下列变化过程得出的函数关系式是否正确,如果错误,请指出正确的结果;如果正确,指出式子中的自变量和因变量.
(1)设一长方体盒子高为10 cm,底面是正方形,这个长方体的体积V(cm3)与底面边长a(cm)的关系式为V=10a2;
(2)某市出租车起步价是7元(路程小于或等于2千米),超过2千米每增加1千米加收1.6元,出租车车费y(元)与行程x(千米)之间的函数关系式为y=1.6(x-2)+7(x≥2);
(3)计划花500元购买篮球,所能购买的总数n(个)与单价a(元)的关系为n=;
(4)用总长为60 m的篱笆围成矩形场地,矩形面积S(m2)与一边长l(m)之间的关系式为S=l(60-l).
4.图3是弹簧挂上重物后,弹簧的长度y(厘米)与所挂物体的质量x(千克)之间的变化关系图.根据图象,回答问题:
图3
(1)不挂重物时,弹簧长多少厘米?
(2)当所挂物体的质量分别为5千克,10千克,15千克,20千克时弹簧的长度分别是多少厘米?
(3)当物体的质量x取0千克至20千克之间任一确定的值时,相应的弹簧的长度y能确定吗?反过来,弹簧的长度y是15~25之间一个确定的值,你能确定所挂重物的质量是多少吗?
(4)弹簧长度y可以看成是物体质量x的函数吗?
5 求下列函数的自变量x的取值范围.
(1);
(2)y=x-1;
(3);
(4)
6.如图,这是某地区一天的气温随时间变化的图象,根据图象回答:在这一天中:
(1)______时气温最高,______时气温最低,最高气温是______,最低气温是______;
(2)20时的气温是______;
(3)______时的气温是6 ℃;
(4)______时间内,气温不断下降;
(5)______时间内,气温持续不变.
【答案】
1.①②③都含有两个变量,①中人均纯收入可以看成年份的函数,②中有效成分释放量是服用后的时间的函数,③中话费是通话时间的函数
2.(1)(2)(3)(4)(7)(8)是函数关系,(5)(6)不是.
3.解:(1)因为长方体的体积为长乘宽乘高,而长、宽、高分别为10、a、a.所以V=10a2正确.自变量是a,因变量是V.
(2)y=1.6(x-2)+7(x≥2)正确,其中x是自变量,y是因变量.
(3)n=正确.
其中a是自变量,n是因变量.
(4)S=l(60-l)错误.
因为60 m是矩形的周长,所以相邻两边的和为30 cm,其中一边长为l (m),则另一边长为(30-l)m,所以S=l(30-l).
4.(1)不挂重物时,弹簧长15 cm.
(2)当所挂重物的质量分别是5千克、10千克、15千克、20千克时,弹簧的长度分别为17.5 cm、20 cm、22.5 cm、25 cm
(3)当x取0~20之间任一确定值时,y都惟一确定;反之也是.
(4)y可以看成是x的函数.
5.分析:如果函数中含有偶次根式,则要求被开方数≥0.
.解:(1)的x的取值范围是:x≥1;
(2)y=x-1的x的取值范围是全体实数;
(3)的x的取值范围是:x≥1;
(4)的x的取值范围是全体实数;
6.(1)16,4,10℃,-4℃ (2)8℃ (3)10 (4)16-24 (5)12-14
设计意图:对求函数的定义域进行方法引导,偶次方根必需注意的地方.
六、课堂小结
本节课应掌握如下内容.
1.初步掌握函数概念,能判断两个变量间的关系是否可看做函数.
2.在一个函数关系式中,能识别自变量与因变量,给定自变量的值,相应地会求出函数的值.
3.函数的三种表达形式
(1)图象;
(2)表格;
(3)代数表达式.
七、板书设计
4.1函数
1.函数
2.表达形式
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
