数学北师大版八年级上册 《探索勾股定理第2课时》精品教案(含答案)
文档属性
| 名称 | 数学北师大版八年级上册 《探索勾股定理第2课时》精品教案(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 567.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览


文档简介
第一章 勾股定理
1探索勾股定理
第2课时
一、教学目标
1.进一步了解勾股定理,探索勾股定理的证明过程.
2.学会利用几何图形的截、割、补证明勾股定理.
3.能够利用勾股定理解决简单的实际问题.
4.在数学活动中发展学生的探究意识和合作交流的习性,体会勾股定理的应用价值.
二、教学重难点
重点:运用割补、拼图的方法证明勾股定理的正确性.
难点:灵活应用勾股定理解决实际问题.
三、教学用具
电脑、多媒体、课件、教学用具等
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
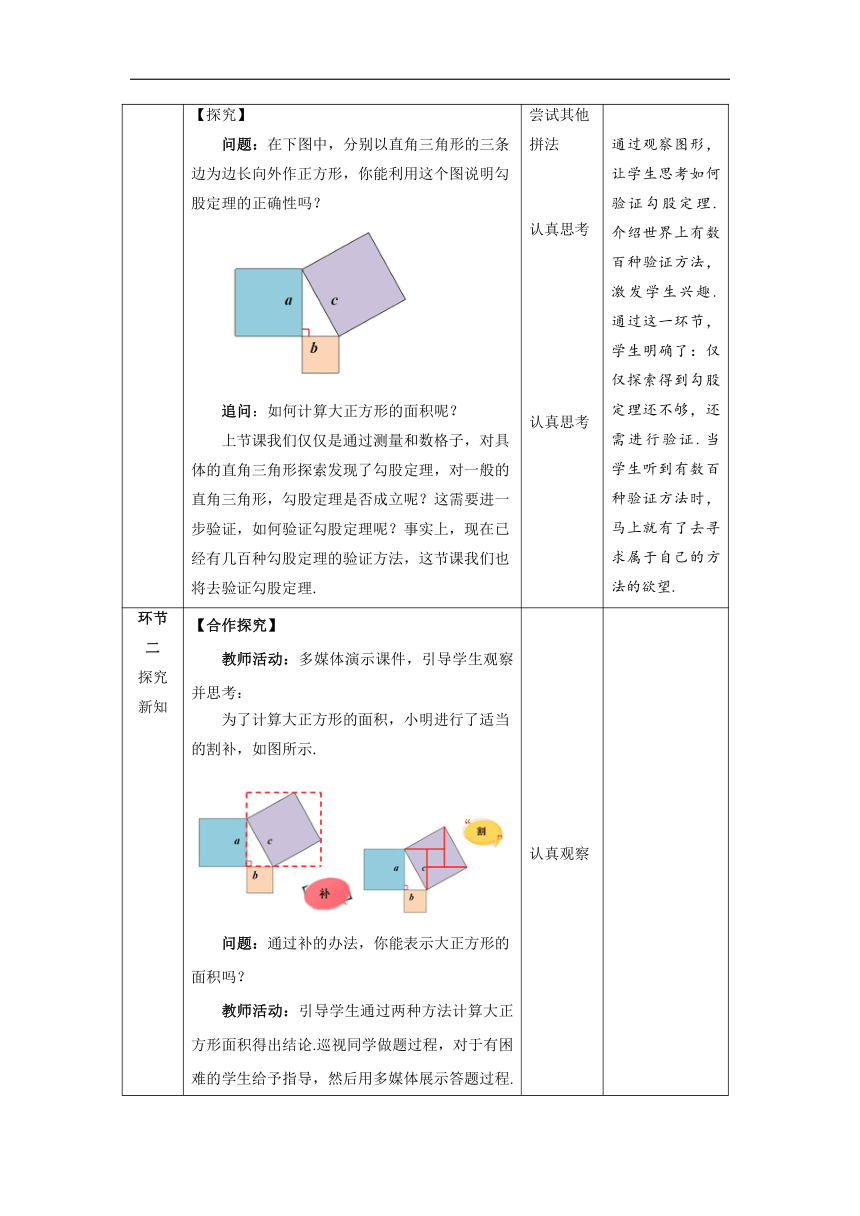
环节一 创设 情境 【操作】 活动:(小组合作展示)今天我们将研究利用拼图的方法验证勾股定理,请你利用自己准备的四个全等的直角三角形,拼出一个以斜边为边长的正方形. 提出问题,观察学生如何操作,再让学生展示过程,最后教师用课件展示拼图过程. 追问:还有其他拼法吗? 【探究】 问题:在下图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗? 追问:如何计算大正方形的面积呢? 上节课我们仅仅是通过测量和数格子,对具体的直角三角形探索发现了勾股定理,对一般的直角三角形,勾股定理是否成立呢?这需要进一步验证,如何验证勾股定理呢?事实上,现在已经有几百种勾股定理的验证方法,这节课我们也将去验证勾股定理. 学生用手中的三角形拼图 尝试其他拼法 认真思考 认真思考 设计活动的目的是为了让学生在活动中体会图形的构成,既为勾股定理的验证作铺垫,同时也培养学生的动手、创新能力. 通过观察图形,让学生思考如何验证勾股定理.介绍世界上有数百种验证方法,激发学生兴趣.通过这一环节,学生明确了:仅仅探索得到勾股定理还不够,还需进行验证.当学生听到有数百种验证方法时,马上就有了去寻求属于自己的方法的欲望.
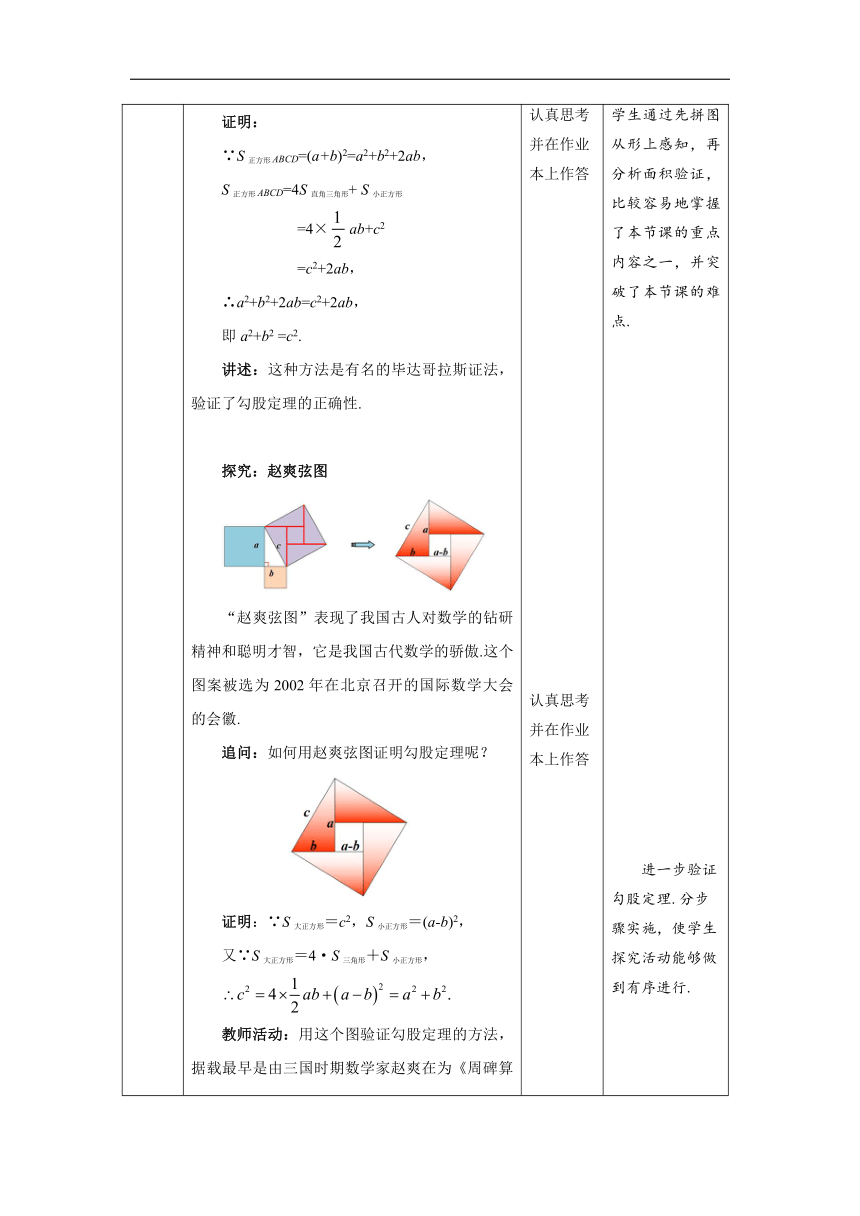
环节二 探究 新知 【合作探究】 教师活动:多媒体演示课件,引导学生观察并思考: 为了计算大正方形的面积,小明进行了适当的割补,如图所示. 问题:通过补的办法,你能表示大正方形的 面积吗? 教师活动:引导学生通过两种方法计算大正方形面积得出结论.巡视同学做题过程,对于有困难的学生给予指导,然后用多媒体展示答题过程. 证明: ∵S正方形ABCD=(a+b)2=a2+b2+2ab, S正方形ABCD=4S直角三角形+ S小正方形 =4×ab+c2 =c2+2ab, ∴a2+b2+2ab=c2+2ab, 即a2+b2 =c2. 讲述:这种方法是有名的毕达哥拉斯证法,验证了勾股定理的正确性. 探究:赵爽弦图 “赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.这个图案被选为2002年在北京召开的国际数学大会的会徽. 追问:如何用赵爽弦图证明勾股定理呢? 证明:∵S大正方形=c2,S小正方形=(a-b)2, 又∵S大正方形=4·S三角形+S小正方形, 教师活动:用这个图验证勾股定理的方法,据载最早是由三国时期数学家赵爽在为《周碑算经》作注时给出的.我国历史上将该图中弦上的正方形称为弦图. 作为国际数学大会的会徽的“弦图”,它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们! 其他证法是怎么样的呢?我们来了解下. 美国第二十任总统伽菲尔德的“总统证法”.如图,图中的三个三角形都是直角三角形,求证:a2+b2 =c2. 多媒体展示答题过程 , 教师活动:事实上,勾股定理的证明方法十分丰富,达数百种之多.其中一种方法尤为独特,单靠移动几块图形就直观地证出了勾股定理,被誉为“无字的证明”,我们欣赏几个! 青朱出入图 达·芬奇证明:根据空白部分面积相等计算即可得证. 做一做 1.图中阴影部分是一个正方形,则此正方形的面积为 . 2.若正方形的面积为8cm2,则正方形对角线长为______cm. 教师活动:先由学生独立完成,教师及时给予指导,在此活动中,教师应重点关注学生能否进一步理解勾股定理的逆定理的用法. 答:(1)36 cm (2)4 认真观察 认真思考并在作业本上作答 认真思考并在作业本上作答 在教师的引导下,认真思考并在作业本上作答 欣赏无字证明勾股定理的方法 认真观察并思考 学生通过先拼图从形上感知,再分析面积验证,比较容易地掌握了本节课的重点内容之一,并突破了本节课的难点. 进一步验证勾股定理.分步骤实施,使学生探究活动能够做到有序进行. 这个环节完全由学生来组织开展,教师可在两天前布置任务,让部分同学收集勾股定理的资料.介绍与勾股定理有关的历史,激发学生的爱国热情;学生加强了对数学史的了解,培养学习数学的兴趣;通过让部分学生搜集材料,展示材料,既可以让学生得到充分的锻炼,同时也可以活跃课堂气氛.
环节三 应用 新知 【典型例题】 教师提出问题,学生先独立思考,解答.然后再小组交流探讨,教师巡视,如遇到有困难的学生适当点拨,最终教师展示答题过程. 【例1】 我方侦察员小王在距离东西向公路400m处侦察,发现一辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗? 教师根据题干分析题中提供的已知条件,并画出图形. 解:由勾股定理,可以得到AB2=BC2+AC2, 即:5002=BC2+4002, ∵BC>0,∴BC=300. 敌方汽车10s行驶了300m,那么它1h行驶的距离为: 300×6×60=108000(m), 即它行驶的速度为108km/h. 【例2】如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长. 教师根据题干分析题中提供的已知条件,并用动画在图上标明. 解:在Rt△ABF中,由勾股定理, 得 BF2=AF2-AB2=102-82 BF=6cm. ∴CF=BC-BF=4. 设EC=xcm,则EF=DE=(8-x) cm, 在Rt△ECF中,根据勾股定理, 得 x2+ 42=(8-x)2 解得 x=3. 所以EC的长为3 cm. 议一议 观察下图,判断图中三角形的三边长是否满足a2+b2 =c2. 结论1:若钝角三角形中较长边长为c,较短边长为a、b,则a2+b2c2. 思考问题,尝试回答问题,明确例题的做法 明确例题的做法 思考问题,尝试回答问题 初步运用勾股定理解决实际问题,培养学生应用数学的意识和能力;体会勾股定理的应用价值,巩固所学知识,加深对勾股定理的逆定理的理解. 给出问题,激发学生思考,并讨论交流.引导学生从数学现象背后发现数学规律,为后面学生独立解题打下一定的基础. 学生通过数格子的方法可以得出:如果不是直角三角形,那么它的三边a,b,c不满足a2+b2 =c2.通过这个结论,学生将对直角三角形三边的关系又进一步的认识,并为后续直角三角形的判定打下基础.
环节四 巩固 新知 教师给出练习,随时观察学生完成情况并相应指导,最后给出答案,根据学生完成情况适当分析讲解. 1. 如图,有两棵树,一棵高10 m,另一棵高4 m,两棵树相距8 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( ) A.8 m B.10m C.12m D.14 m 2.如果梯子的底端离一幢楼5米,那么13米长的梯子可以达到该楼的高度是( ) A.12米 B.13米 C.14米 D.15米 3.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是________. 如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB ⊥AB, DA=15km,CB= 10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E站应建在距A站多远处 答案: 1.B; 2. A 3. 200m2; 4.解:如下图,连接DE、CE. 设AE长为x千米, 则EB长为(25-x)千米. 由题意得: 解得:x=10. 答:E站应建在距A站10千米处. 自主完成练习,然后集体交流评价. 通过课堂练习及时巩固本节课所学内容,并考查学生的知识应用能力,培养独立完成练习的习惯.
环节五 课堂 小结 思维导图的形式呈现本节课的主要内容: 回顾本节课所讲的内容 通过小结总结回顾本节课学习内容,帮助学生归纳、巩固所学知识.
环节六 布置 作业 教科书第7页 习题1.2 第1、3题 课后完成练习 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
1探索勾股定理
第2课时
一、教学目标
1.进一步了解勾股定理,探索勾股定理的证明过程.
2.学会利用几何图形的截、割、补证明勾股定理.
3.能够利用勾股定理解决简单的实际问题.
4.在数学活动中发展学生的探究意识和合作交流的习性,体会勾股定理的应用价值.
二、教学重难点
重点:运用割补、拼图的方法证明勾股定理的正确性.
难点:灵活应用勾股定理解决实际问题.
三、教学用具
电脑、多媒体、课件、教学用具等
四、教学过程设计
教学 环节 教师活动 学生活动 设计意图
环节一 创设 情境 【操作】 活动:(小组合作展示)今天我们将研究利用拼图的方法验证勾股定理,请你利用自己准备的四个全等的直角三角形,拼出一个以斜边为边长的正方形. 提出问题,观察学生如何操作,再让学生展示过程,最后教师用课件展示拼图过程. 追问:还有其他拼法吗? 【探究】 问题:在下图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗? 追问:如何计算大正方形的面积呢? 上节课我们仅仅是通过测量和数格子,对具体的直角三角形探索发现了勾股定理,对一般的直角三角形,勾股定理是否成立呢?这需要进一步验证,如何验证勾股定理呢?事实上,现在已经有几百种勾股定理的验证方法,这节课我们也将去验证勾股定理. 学生用手中的三角形拼图 尝试其他拼法 认真思考 认真思考 设计活动的目的是为了让学生在活动中体会图形的构成,既为勾股定理的验证作铺垫,同时也培养学生的动手、创新能力. 通过观察图形,让学生思考如何验证勾股定理.介绍世界上有数百种验证方法,激发学生兴趣.通过这一环节,学生明确了:仅仅探索得到勾股定理还不够,还需进行验证.当学生听到有数百种验证方法时,马上就有了去寻求属于自己的方法的欲望.
环节二 探究 新知 【合作探究】 教师活动:多媒体演示课件,引导学生观察并思考: 为了计算大正方形的面积,小明进行了适当的割补,如图所示. 问题:通过补的办法,你能表示大正方形的 面积吗? 教师活动:引导学生通过两种方法计算大正方形面积得出结论.巡视同学做题过程,对于有困难的学生给予指导,然后用多媒体展示答题过程. 证明: ∵S正方形ABCD=(a+b)2=a2+b2+2ab, S正方形ABCD=4S直角三角形+ S小正方形 =4×ab+c2 =c2+2ab, ∴a2+b2+2ab=c2+2ab, 即a2+b2 =c2. 讲述:这种方法是有名的毕达哥拉斯证法,验证了勾股定理的正确性. 探究:赵爽弦图 “赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲.这个图案被选为2002年在北京召开的国际数学大会的会徽. 追问:如何用赵爽弦图证明勾股定理呢? 证明:∵S大正方形=c2,S小正方形=(a-b)2, 又∵S大正方形=4·S三角形+S小正方形, 教师活动:用这个图验证勾股定理的方法,据载最早是由三国时期数学家赵爽在为《周碑算经》作注时给出的.我国历史上将该图中弦上的正方形称为弦图. 作为国际数学大会的会徽的“弦图”,它既标志着中国古代的数学成就,又像一只转动的风车,欢迎来自世界各地的数学家们! 其他证法是怎么样的呢?我们来了解下. 美国第二十任总统伽菲尔德的“总统证法”.如图,图中的三个三角形都是直角三角形,求证:a2+b2 =c2. 多媒体展示答题过程 , 教师活动:事实上,勾股定理的证明方法十分丰富,达数百种之多.其中一种方法尤为独特,单靠移动几块图形就直观地证出了勾股定理,被誉为“无字的证明”,我们欣赏几个! 青朱出入图 达·芬奇证明:根据空白部分面积相等计算即可得证. 做一做 1.图中阴影部分是一个正方形,则此正方形的面积为 . 2.若正方形的面积为8cm2,则正方形对角线长为______cm. 教师活动:先由学生独立完成,教师及时给予指导,在此活动中,教师应重点关注学生能否进一步理解勾股定理的逆定理的用法. 答:(1)36 cm (2)4 认真观察 认真思考并在作业本上作答 认真思考并在作业本上作答 在教师的引导下,认真思考并在作业本上作答 欣赏无字证明勾股定理的方法 认真观察并思考 学生通过先拼图从形上感知,再分析面积验证,比较容易地掌握了本节课的重点内容之一,并突破了本节课的难点. 进一步验证勾股定理.分步骤实施,使学生探究活动能够做到有序进行. 这个环节完全由学生来组织开展,教师可在两天前布置任务,让部分同学收集勾股定理的资料.介绍与勾股定理有关的历史,激发学生的爱国热情;学生加强了对数学史的了解,培养学习数学的兴趣;通过让部分学生搜集材料,展示材料,既可以让学生得到充分的锻炼,同时也可以活跃课堂气氛.
环节三 应用 新知 【典型例题】 教师提出问题,学生先独立思考,解答.然后再小组交流探讨,教师巡视,如遇到有困难的学生适当点拨,最终教师展示答题过程. 【例1】 我方侦察员小王在距离东西向公路400m处侦察,发现一辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗? 教师根据题干分析题中提供的已知条件,并画出图形. 解:由勾股定理,可以得到AB2=BC2+AC2, 即:5002=BC2+4002, ∵BC>0,∴BC=300. 敌方汽车10s行驶了300m,那么它1h行驶的距离为: 300×6×60=108000(m), 即它行驶的速度为108km/h. 【例2】如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长. 教师根据题干分析题中提供的已知条件,并用动画在图上标明. 解:在Rt△ABF中,由勾股定理, 得 BF2=AF2-AB2=102-82 BF=6cm. ∴CF=BC-BF=4. 设EC=xcm,则EF=DE=(8-x) cm, 在Rt△ECF中,根据勾股定理, 得 x2+ 42=(8-x)2 解得 x=3. 所以EC的长为3 cm. 议一议 观察下图,判断图中三角形的三边长是否满足a2+b2 =c2. 结论1:若钝角三角形中较长边长为c,较短边长为a、b,则a2+b2
环节四 巩固 新知 教师给出练习,随时观察学生完成情况并相应指导,最后给出答案,根据学生完成情况适当分析讲解. 1. 如图,有两棵树,一棵高10 m,另一棵高4 m,两棵树相距8 m,一只小鸟从一棵树的树顶飞到另一棵树的树顶,小鸟至少飞行( ) A.8 m B.10m C.12m D.14 m 2.如果梯子的底端离一幢楼5米,那么13米长的梯子可以达到该楼的高度是( ) A.12米 B.13米 C.14米 D.15米 3.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是________. 如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB ⊥AB, DA=15km,CB= 10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E站应建在距A站多远处 答案: 1.B; 2. A 3. 200m2; 4.解:如下图,连接DE、CE. 设AE长为x千米, 则EB长为(25-x)千米. 由题意得: 解得:x=10. 答:E站应建在距A站10千米处. 自主完成练习,然后集体交流评价. 通过课堂练习及时巩固本节课所学内容,并考查学生的知识应用能力,培养独立完成练习的习惯.
环节五 课堂 小结 思维导图的形式呈现本节课的主要内容: 回顾本节课所讲的内容 通过小结总结回顾本节课学习内容,帮助学生归纳、巩固所学知识.
环节六 布置 作业 教科书第7页 习题1.2 第1、3题 课后完成练习 通过课后作业,教师能及时了解学生对本节课知识的掌握情况,以便对教学进度和方法进行适当的调整.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
