5.3诱导公式 课件(共23张PPT)
文档属性
| 名称 | 5.3诱导公式 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览



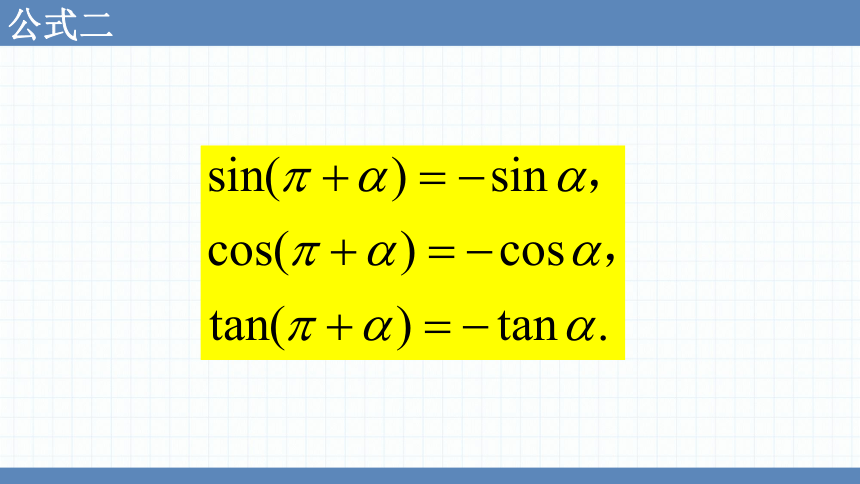



文档简介
(共23张PPT)
5.3诱导公式
新课引入
新课引入
设P1(z1,y1),P2(x2,y2),因为P2是点P1关于原点的对称点所以
x2=-x1,y2=-y1.
可得:
公式二
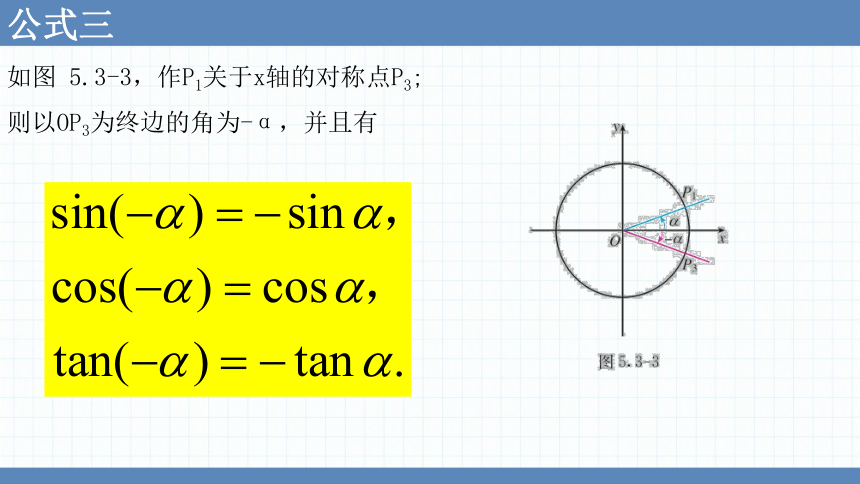
公式三
如图 5.3-3,作P1关于x轴的对称点P3;
则以OP3为终边的角为-α,并且有
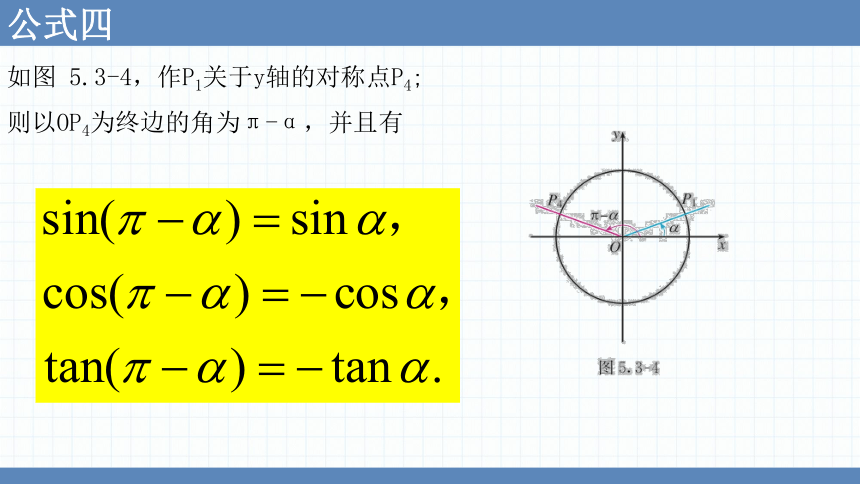
公式四
如图 5.3-4,作P1关于y轴的对称点P4;
则以OP4为终边的角为π-α,并且有
公式三、四的证明
请你类比公式二,证明公式三和公式四
例题巩固
思考:由例1,你对公式一~公式四的作用有什么进一步的认识?你能自己归纳一下任意角的三角函数转化为锐角三角函数的步骤吗?
例题巩固
例题巩固
公式五
设 P5(x5,y5),由于P5是点P1关于直线 y=x的对称点,可以证明
x5=y1,y5=x1.
根据三角函数的定义,得:
公式五
公式六
公式一~公式六都叫做诱导公式 (induction formula).
例题巩固
知识填空
回顾诱导公式一~六
课堂检测
课堂检测
课堂检测
课堂检测
课堂检测
课堂小结
学生回顾思考知识点
教师补充归纳总结
布置作业
课时作业5.3
谢谢!
布置作业
◆
E-MA2
-
○
然
C
5.3诱导公式
前面利用圆的几何性质,得到了同角三角函数之间的基
本关系.我们知道,圆的最重要的性质是对称性,而对称性
(如奇偶性)也是函数的重要性质.由此想到,可以利用圆
的对称性,研究三角函数的对称性
公探究1
如图5.3-1,在直角坐标系内,设任意角α的
终边与单位圆交于点P1.
(1)作P1关于原点的对称点P2,以OP2为
终边的角P与角α有什么关系?角B,α的三角函
数值之间有什么关系?
(2)如果作P1关于x轴(或y轴)的对称点
P3(或P4),那么又可以得到什么结论?
图5.3-1
下面,借助单位圆的对称性进行探究
如图5.3-2,以OP2为终边的角B都是与角π十a
y
终边相同的角,即B=2kπ十(π十a)(k∈Z).因此,
只要探究角π十a与a的三角函数值之间的关系
即可.
+C
设P1(x1,y1),P2(x2,y2).因为P2是点P
关于原点的对称点,所以
x2=一x1,y2=一y1.
根据三角函数的定义,得
图5.3-2
sin a=y1,
cOS =x1,
tan a=yI
●
●
sn(r+a)=y2,cos(x+a)=r2,tan(x十a)=当
角π十a还可以看作
是角Q的终边按逆时针方
从而得
向旋转角π得到的.
188第五章三角函数
5.3诱导公式
新课引入
新课引入
设P1(z1,y1),P2(x2,y2),因为P2是点P1关于原点的对称点所以
x2=-x1,y2=-y1.
可得:
公式二
公式三
如图 5.3-3,作P1关于x轴的对称点P3;
则以OP3为终边的角为-α,并且有
公式四
如图 5.3-4,作P1关于y轴的对称点P4;
则以OP4为终边的角为π-α,并且有
公式三、四的证明
请你类比公式二,证明公式三和公式四
例题巩固
思考:由例1,你对公式一~公式四的作用有什么进一步的认识?你能自己归纳一下任意角的三角函数转化为锐角三角函数的步骤吗?
例题巩固
例题巩固
公式五
设 P5(x5,y5),由于P5是点P1关于直线 y=x的对称点,可以证明
x5=y1,y5=x1.
根据三角函数的定义,得:
公式五
公式六
公式一~公式六都叫做诱导公式 (induction formula).
例题巩固
知识填空
回顾诱导公式一~六
课堂检测
课堂检测
课堂检测
课堂检测
课堂检测
课堂小结
学生回顾思考知识点
教师补充归纳总结
布置作业
课时作业5.3
谢谢!
布置作业
◆
E-MA2
-
○
然
C
5.3诱导公式
前面利用圆的几何性质,得到了同角三角函数之间的基
本关系.我们知道,圆的最重要的性质是对称性,而对称性
(如奇偶性)也是函数的重要性质.由此想到,可以利用圆
的对称性,研究三角函数的对称性
公探究1
如图5.3-1,在直角坐标系内,设任意角α的
终边与单位圆交于点P1.
(1)作P1关于原点的对称点P2,以OP2为
终边的角P与角α有什么关系?角B,α的三角函
数值之间有什么关系?
(2)如果作P1关于x轴(或y轴)的对称点
P3(或P4),那么又可以得到什么结论?
图5.3-1
下面,借助单位圆的对称性进行探究
如图5.3-2,以OP2为终边的角B都是与角π十a
y
终边相同的角,即B=2kπ十(π十a)(k∈Z).因此,
只要探究角π十a与a的三角函数值之间的关系
即可.
+C
设P1(x1,y1),P2(x2,y2).因为P2是点P
关于原点的对称点,所以
x2=一x1,y2=一y1.
根据三角函数的定义,得
图5.3-2
sin a=y1,
cOS =x1,
tan a=yI
●
●
sn(r+a)=y2,cos(x+a)=r2,tan(x十a)=当
角π十a还可以看作
是角Q的终边按逆时针方
从而得
向旋转角π得到的.
188第五章三角函数
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
