第5章 二元一次方程组 课后复习题 北师大版八年级数学上册(含答案)
文档属性
| 名称 | 第5章 二元一次方程组 课后复习题 北师大版八年级数学上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 113.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览




文档简介
第5章 二元一次方程组(课后复习题)-北师大版八年级上册
一.选择题
.已知是方程组的解,则a﹣b的值是( )
A.﹣1 B.2 C.3 D.4
.若关于x,y的方程组的解适合方程x+y=﹣2,则m的值为( )
A.﹣3 B.1 C.2 D.3
.已知方程组的解都为非负数,若w=3x﹣2y﹣7z+7,则w的最大值是( )
A.﹣4 B.﹣8 C.﹣2 D.以上都不对
.为了加大“精准扶贫”力度,某市准备将10名干部分成2人一组或3人一组,到村屯带领贫困户脱贫,在所有干部都参加且每人只能参加一个小组的前提下,分组方案有( )
A.1种 B.2种 C.3种 D.4种
.某校学生去看电影,如果每辆汽车坐60人,则空出1辆汽车,如果每辆汽车坐45人,则15人没有座位,那么学生人数和汽车辆数各是多少?( )
A.230人、6辆 B.240人、5辆 C.240人、8辆 D.250人、7辆
.在解二元一次方程组时,我们常常采用的方法是消元法,将二元一次方程组转化为一元一次方程求解.下面是甲、乙两个同学解方程组的解题思路:甲同学:①+②,得9x+9y=54③.③×﹣①得到一元一次方程再求解.乙同学:②﹣①×2,得3x﹣6y=0③.由③,得x=2y.再代入原方程组中的任意一个方程中,转化为一元一次方程求解.
通过阅读可知,下列对甲、乙两同学的思路判断正确的是( )
A.只有甲同学的思路正确
B.只有乙同学的思路正确
C.甲、乙两同学的思路都不正确
D.甲、乙两同学的思路都正确
.在解一元二次方程组时,若①﹣②可直接消去未知数y,则 和 ( )
A.互为倒数 B.大小相等 C.互为相反数 D.都等于0
.已知方程组,若用“加减法”消去y,下列做法正确的是( )
A.①+② B.①+②×2 C.①﹣② D.①﹣②×2
.一道来自课本的习题:
从甲地到乙地先有一段上坡路后有一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54分钟,从乙地到甲地需42分钟,甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,采用间接设法:
设坡路有xkm,平路有ykm,则全程为(x+y)km.已经列出一个方程=,则另一个方程正确的是( )
A.= B. C. D.=
10.老师设计了一个解方程组的接力游戏,学习小组的四个成员每人做一步,每人只能看到前一人给的步骤,并进行下一步计算,再将结果传递给下一个人,用合作的方式完成该方程组的解题过程,过程如图所示,合作中出现错误的同学是( )
A.甲 B.丙 C.乙和丁 D.甲和丙
二.填空题
.《九章算术》卷八方程【七】中记载:“今有牛五、羊二,值金十两.牛二、羊五,值金八两.牛、羊各值金几何?”题目大意是:5头牛、2只羊共值金10两,2头牛、5只羊共值金8两,每头牛、每只羊各值金多少两?若设一头牛值金x两,一只羊值金y两,则可列方程组为 .
.对于任意非零实数x,y,定义新运算“ ”:x y=ax﹣by.若2 3=2,3 5=2,则4 6= .
.已知a、b、c满足a+2b+3c=10,3a+2b+c=70,则a+b+c= .
.为了节省空间,家里的饭碗一般是摞起来存放的,如果5只饭碗摞起来的高度为13cm,9只饭碗摞起来的高度为20cm,李老师家碗橱每格的高度为30cm,则李老师一摞碗最多只能放 只.
.已知关于x,y的方程组
(1)若方程组的解为,则a的值为 ;
(2)若x+y=﹣3,则a的值为 .
三.解答题
.解下列方程组:
;
.
.已知关于x,y的方程组.若原方程组的解也是二元一次方程2x+y=3的一个解,求m的值;
.已知关于x、y方程组.
(1)用a表示x、y.
(2)若x2+y2﹣3=4a2,求a4﹣4a2+4a+1的值.
(3)若xy+3n2+m2+18=3n,且n﹣a=2,求m、n的值.
.“当好东道主,文明迎亚运”,本区对亚运场馆附近的主干道进行了改造,因道路建设需要开挖土石方,计划每小时挖掘土石方1760m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
租金(单位:元/台 时) 挖掘土石方量(单位:m3/台 时)
甲型 190 160
乙型 260 240
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过2000元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
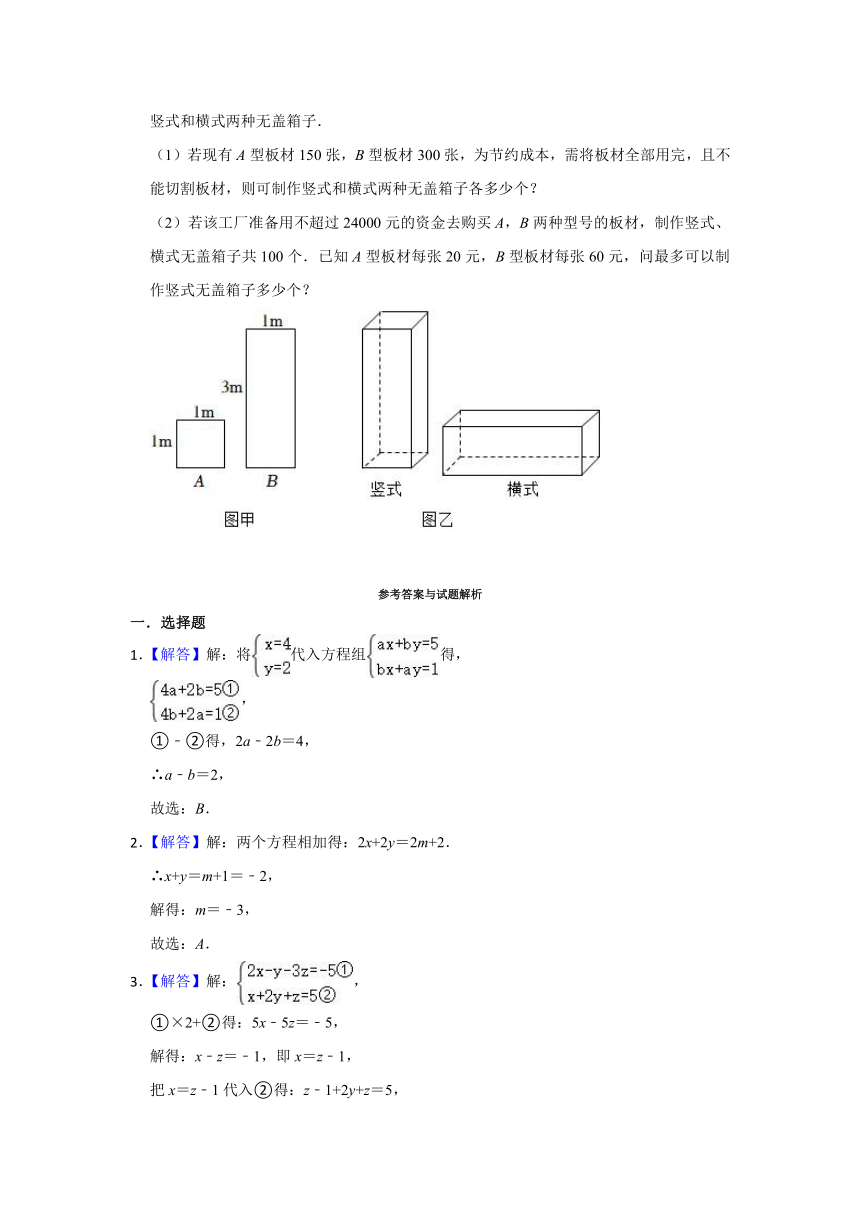
20.某工厂准备用如图甲所示的A型正方形板材和B型长方形板材,制作成如图乙所示的竖式和横式两种无盖箱子.
(1)若现有A型板材150张,B型板材300张,为节约成本,需将板材全部用完,且不能切割板材,则可制作竖式和横式两种无盖箱子各多少个?
(2)若该工厂准备用不超过24000元的资金去购买A,B两种型号的板材,制作竖式、横式无盖箱子共100个.已知A型板材每张20元,B型板材每张60元,问最多可以制作竖式无盖箱子多少个?
参考答案与试题解析
一.选择题
.【解答】解:将代入方程组得,
,
①﹣②得,2a﹣2b=4,
∴a﹣b=2,
故选:B.
.【解答】解:两个方程相加得:2x+2y=2m+2.
∴x+y=m+1=﹣2,
解得:m=﹣3,
故选:A.
.【解答】解:,
①×2+②得:5x﹣5z=﹣5,
解得:x﹣z=﹣1,即x=z﹣1,
把x=z﹣1代入②得:z﹣1+2y+z=5,
解得:y=﹣z+3,
代入得:w=3(z﹣1)﹣2(﹣z+3)﹣7z+7=3z﹣3+2z﹣6﹣7z+7=﹣2z﹣2,
∵z为非负数,即z≥0,
∴﹣2z≤0,即﹣2z﹣2≤﹣2,
则w的最大值为﹣2.
故选:C.
.【解答】解:设可以分成2人组x组,3人组y组,
依题意得:2x+3y=10,
∴x=5﹣y,
又∵x,y均为自然数,
∴或,
∴共有2种分组方案.
故选:B.
.【解答】解:设一共x人,y辆汽车,
根据题意得:,
解得:.
答:一共240人,5辆汽车.
故选:B.
.【解答】解:解方程组的解题思路:
甲同学:①+②得:9x+9y=54③,
③×﹣①得:﹣3y=﹣6,
解得:y=2,
把y=2代入①得:2x+10=18,
解得:x=4,
则方程组的解为;
乙同学:②﹣①×2得:3x﹣6y=0③,
由③得:x=2y,
代入①得:4y+5y=18,
解得:y=2,
把y=2代入得:x=4,
则方程组的解为,
则甲、乙两同学的思路都正确.
故选:D.
.【解答】解:在解一元二次方程组时,
若①﹣②可直接消去未知数y,则 和 大小相等.
故选:B.
.【解答】解:方程组,
若用“加减法”消去y,可以采用①+②×2.
故选:B.
.【解答】解:依题意有:另一个方程正确的是+=.
故选:B.
.【解答】解:,
由①得:x=③,
把③代入②得:3 ﹣5y=5,
去分母得:24﹣9y﹣10y=10,
解得:y=,
把y=代入③得:x==4﹣=,
则合作中出现错误的同学是丙同学.
故选:B.
二.填空题
.【解答】解:由题意可得,,
故答案为:.
.【解答】解:由题意得:
,
解这个方程组得:,
∴4 6
=4a﹣6b
=4×4﹣6×2
=16﹣12
=4.
故答案为:4.
.【解答】解:a、b、c满足a+2b+3c=10①,3a+2b+c=70②,
①+②得,4a+4b+4c=80,
所以a+b+c=20,
故答案为:20.
.【解答】解:一只碗的高度是xcm,每摞起来一只碗增加ycm,
则;
解得:,
∴30﹣6=14(只),
答:李老师一摞碗最多只能放14只.
故答案为:14.
.【解答】解:(1)∵方程组的解为,
∴2×2+(﹣1)=2a+1,
∴2a=2,
∴a=1.
故答案为:1;
(2)由题意得:
,
解得:,
∴2×(﹣6)+3=2a+1,
∴2a=﹣10,
∴a=﹣5.
故答案为:﹣5.
三.解答题
.【解答】解:(1),
①+②×5得:13x=78,
解得:x=6,
把x=6代入②得:12+y=15,
解得:y=3,
则方程组的解为;
(2),
①+②×4得:23x=23,
解得:x=1,
把x=1代入②得:5﹣y=3,
解得:y=2,
则方程组的解为.
.【解答】解:,
①+②得:2x+y=2+m,
代入方程2x+y=3得:2+m=3,
解得:m=1.
.【解答】解:(1),
①﹣②得,4y=4﹣4a,
解得y=1﹣a,
把y=1﹣a代入②得,x﹣1+a=3a,
解得x=1+2a,
∴;
(2)将代入x2+y2﹣3=4a2,
得(1+2a)2+(1﹣a)2﹣3=4a2,
化简得a2=1﹣2a,
a4﹣4a2+4a+1
=(a2)2﹣4a2+4a+1
=(1﹣2a)2﹣4a2+4a+1
=1﹣4a+4a2﹣4a2+4a+1
=2;
(3)∵,n﹣a=2,
∴,
把x,y代入xy+3n2+m2+18=3n中,
得(2n﹣3)(3﹣n)+3n2+m2+18=3n,
化简得n2+6n+9+m2=0,
即(n+3)2+m2=0,
∴n=﹣3,m=0.
.【解答】解:(1)设需租用甲型号的挖掘机x台,乙型号的挖掘机y台,
依题意得:,
解得:.
答:需租用甲型号的挖掘机2台,乙型号的挖掘机6台.
(2)设需租用甲型号的挖掘机m台,乙型号的挖掘机n台,
依题意得:160m+240n=1760,
∴m=11﹣n.
又∵m,n均为正整数,
∴或或.
①当m=8,n=2时,每小时需支付的租金为190×8+260×2=2040(元),2040>2000,不符合题意,舍去;
②当m=5,n=4时,每小时需支付的租金为190×5+260×4=1990(元),1990<2000,符合题意;
③当m=2,n=6时,每小时需支付的租金为190×2+260×6=1940(元),1940<2000,符合题意.
答:共有2种不同的租用方案.
.【解答】解:(1)设可制作竖式无盖箱子x个,横式无盖箱子y个,
依题意得:,
解得:,
答:可制作竖式无盖箱子30个,横式无盖箱子60个.
(2)设制作竖式无盖箱子m个,则制作横式无盖箱子(100﹣m)个,
依题意得:20×[m+2(100﹣m)]+60×[4m+3(100﹣m)]≤24000,
解得:m≤50.
答:最多可以制作竖式无盖箱子50个.
一.选择题
.已知是方程组的解,则a﹣b的值是( )
A.﹣1 B.2 C.3 D.4
.若关于x,y的方程组的解适合方程x+y=﹣2,则m的值为( )
A.﹣3 B.1 C.2 D.3
.已知方程组的解都为非负数,若w=3x﹣2y﹣7z+7,则w的最大值是( )
A.﹣4 B.﹣8 C.﹣2 D.以上都不对
.为了加大“精准扶贫”力度,某市准备将10名干部分成2人一组或3人一组,到村屯带领贫困户脱贫,在所有干部都参加且每人只能参加一个小组的前提下,分组方案有( )
A.1种 B.2种 C.3种 D.4种
.某校学生去看电影,如果每辆汽车坐60人,则空出1辆汽车,如果每辆汽车坐45人,则15人没有座位,那么学生人数和汽车辆数各是多少?( )
A.230人、6辆 B.240人、5辆 C.240人、8辆 D.250人、7辆
.在解二元一次方程组时,我们常常采用的方法是消元法,将二元一次方程组转化为一元一次方程求解.下面是甲、乙两个同学解方程组的解题思路:甲同学:①+②,得9x+9y=54③.③×﹣①得到一元一次方程再求解.乙同学:②﹣①×2,得3x﹣6y=0③.由③,得x=2y.再代入原方程组中的任意一个方程中,转化为一元一次方程求解.
通过阅读可知,下列对甲、乙两同学的思路判断正确的是( )
A.只有甲同学的思路正确
B.只有乙同学的思路正确
C.甲、乙两同学的思路都不正确
D.甲、乙两同学的思路都正确
.在解一元二次方程组时,若①﹣②可直接消去未知数y,则 和 ( )
A.互为倒数 B.大小相等 C.互为相反数 D.都等于0
.已知方程组,若用“加减法”消去y,下列做法正确的是( )
A.①+② B.①+②×2 C.①﹣② D.①﹣②×2
.一道来自课本的习题:
从甲地到乙地先有一段上坡路后有一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54分钟,从乙地到甲地需42分钟,甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,采用间接设法:
设坡路有xkm,平路有ykm,则全程为(x+y)km.已经列出一个方程=,则另一个方程正确的是( )
A.= B. C. D.=
10.老师设计了一个解方程组的接力游戏,学习小组的四个成员每人做一步,每人只能看到前一人给的步骤,并进行下一步计算,再将结果传递给下一个人,用合作的方式完成该方程组的解题过程,过程如图所示,合作中出现错误的同学是( )
A.甲 B.丙 C.乙和丁 D.甲和丙
二.填空题
.《九章算术》卷八方程【七】中记载:“今有牛五、羊二,值金十两.牛二、羊五,值金八两.牛、羊各值金几何?”题目大意是:5头牛、2只羊共值金10两,2头牛、5只羊共值金8两,每头牛、每只羊各值金多少两?若设一头牛值金x两,一只羊值金y两,则可列方程组为 .
.对于任意非零实数x,y,定义新运算“ ”:x y=ax﹣by.若2 3=2,3 5=2,则4 6= .
.已知a、b、c满足a+2b+3c=10,3a+2b+c=70,则a+b+c= .
.为了节省空间,家里的饭碗一般是摞起来存放的,如果5只饭碗摞起来的高度为13cm,9只饭碗摞起来的高度为20cm,李老师家碗橱每格的高度为30cm,则李老师一摞碗最多只能放 只.
.已知关于x,y的方程组
(1)若方程组的解为,则a的值为 ;
(2)若x+y=﹣3,则a的值为 .
三.解答题
.解下列方程组:
;
.
.已知关于x,y的方程组.若原方程组的解也是二元一次方程2x+y=3的一个解,求m的值;
.已知关于x、y方程组.
(1)用a表示x、y.
(2)若x2+y2﹣3=4a2,求a4﹣4a2+4a+1的值.
(3)若xy+3n2+m2+18=3n,且n﹣a=2,求m、n的值.
.“当好东道主,文明迎亚运”,本区对亚运场馆附近的主干道进行了改造,因道路建设需要开挖土石方,计划每小时挖掘土石方1760m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:
租金(单位:元/台 时) 挖掘土石方量(单位:m3/台 时)
甲型 190 160
乙型 260 240
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过2000元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
20.某工厂准备用如图甲所示的A型正方形板材和B型长方形板材,制作成如图乙所示的竖式和横式两种无盖箱子.
(1)若现有A型板材150张,B型板材300张,为节约成本,需将板材全部用完,且不能切割板材,则可制作竖式和横式两种无盖箱子各多少个?
(2)若该工厂准备用不超过24000元的资金去购买A,B两种型号的板材,制作竖式、横式无盖箱子共100个.已知A型板材每张20元,B型板材每张60元,问最多可以制作竖式无盖箱子多少个?
参考答案与试题解析
一.选择题
.【解答】解:将代入方程组得,
,
①﹣②得,2a﹣2b=4,
∴a﹣b=2,
故选:B.
.【解答】解:两个方程相加得:2x+2y=2m+2.
∴x+y=m+1=﹣2,
解得:m=﹣3,
故选:A.
.【解答】解:,
①×2+②得:5x﹣5z=﹣5,
解得:x﹣z=﹣1,即x=z﹣1,
把x=z﹣1代入②得:z﹣1+2y+z=5,
解得:y=﹣z+3,
代入得:w=3(z﹣1)﹣2(﹣z+3)﹣7z+7=3z﹣3+2z﹣6﹣7z+7=﹣2z﹣2,
∵z为非负数,即z≥0,
∴﹣2z≤0,即﹣2z﹣2≤﹣2,
则w的最大值为﹣2.
故选:C.
.【解答】解:设可以分成2人组x组,3人组y组,
依题意得:2x+3y=10,
∴x=5﹣y,
又∵x,y均为自然数,
∴或,
∴共有2种分组方案.
故选:B.
.【解答】解:设一共x人,y辆汽车,
根据题意得:,
解得:.
答:一共240人,5辆汽车.
故选:B.
.【解答】解:解方程组的解题思路:
甲同学:①+②得:9x+9y=54③,
③×﹣①得:﹣3y=﹣6,
解得:y=2,
把y=2代入①得:2x+10=18,
解得:x=4,
则方程组的解为;
乙同学:②﹣①×2得:3x﹣6y=0③,
由③得:x=2y,
代入①得:4y+5y=18,
解得:y=2,
把y=2代入得:x=4,
则方程组的解为,
则甲、乙两同学的思路都正确.
故选:D.
.【解答】解:在解一元二次方程组时,
若①﹣②可直接消去未知数y,则 和 大小相等.
故选:B.
.【解答】解:方程组,
若用“加减法”消去y,可以采用①+②×2.
故选:B.
.【解答】解:依题意有:另一个方程正确的是+=.
故选:B.
.【解答】解:,
由①得:x=③,
把③代入②得:3 ﹣5y=5,
去分母得:24﹣9y﹣10y=10,
解得:y=,
把y=代入③得:x==4﹣=,
则合作中出现错误的同学是丙同学.
故选:B.
二.填空题
.【解答】解:由题意可得,,
故答案为:.
.【解答】解:由题意得:
,
解这个方程组得:,
∴4 6
=4a﹣6b
=4×4﹣6×2
=16﹣12
=4.
故答案为:4.
.【解答】解:a、b、c满足a+2b+3c=10①,3a+2b+c=70②,
①+②得,4a+4b+4c=80,
所以a+b+c=20,
故答案为:20.
.【解答】解:一只碗的高度是xcm,每摞起来一只碗增加ycm,
则;
解得:,
∴30﹣6=14(只),
答:李老师一摞碗最多只能放14只.
故答案为:14.
.【解答】解:(1)∵方程组的解为,
∴2×2+(﹣1)=2a+1,
∴2a=2,
∴a=1.
故答案为:1;
(2)由题意得:
,
解得:,
∴2×(﹣6)+3=2a+1,
∴2a=﹣10,
∴a=﹣5.
故答案为:﹣5.
三.解答题
.【解答】解:(1),
①+②×5得:13x=78,
解得:x=6,
把x=6代入②得:12+y=15,
解得:y=3,
则方程组的解为;
(2),
①+②×4得:23x=23,
解得:x=1,
把x=1代入②得:5﹣y=3,
解得:y=2,
则方程组的解为.
.【解答】解:,
①+②得:2x+y=2+m,
代入方程2x+y=3得:2+m=3,
解得:m=1.
.【解答】解:(1),
①﹣②得,4y=4﹣4a,
解得y=1﹣a,
把y=1﹣a代入②得,x﹣1+a=3a,
解得x=1+2a,
∴;
(2)将代入x2+y2﹣3=4a2,
得(1+2a)2+(1﹣a)2﹣3=4a2,
化简得a2=1﹣2a,
a4﹣4a2+4a+1
=(a2)2﹣4a2+4a+1
=(1﹣2a)2﹣4a2+4a+1
=1﹣4a+4a2﹣4a2+4a+1
=2;
(3)∵,n﹣a=2,
∴,
把x,y代入xy+3n2+m2+18=3n中,
得(2n﹣3)(3﹣n)+3n2+m2+18=3n,
化简得n2+6n+9+m2=0,
即(n+3)2+m2=0,
∴n=﹣3,m=0.
.【解答】解:(1)设需租用甲型号的挖掘机x台,乙型号的挖掘机y台,
依题意得:,
解得:.
答:需租用甲型号的挖掘机2台,乙型号的挖掘机6台.
(2)设需租用甲型号的挖掘机m台,乙型号的挖掘机n台,
依题意得:160m+240n=1760,
∴m=11﹣n.
又∵m,n均为正整数,
∴或或.
①当m=8,n=2时,每小时需支付的租金为190×8+260×2=2040(元),2040>2000,不符合题意,舍去;
②当m=5,n=4时,每小时需支付的租金为190×5+260×4=1990(元),1990<2000,符合题意;
③当m=2,n=6时,每小时需支付的租金为190×2+260×6=1940(元),1940<2000,符合题意.
答:共有2种不同的租用方案.
.【解答】解:(1)设可制作竖式无盖箱子x个,横式无盖箱子y个,
依题意得:,
解得:,
答:可制作竖式无盖箱子30个,横式无盖箱子60个.
(2)设制作竖式无盖箱子m个,则制作横式无盖箱子(100﹣m)个,
依题意得:20×[m+2(100﹣m)]+60×[4m+3(100﹣m)]≤24000,
解得:m≤50.
答:最多可以制作竖式无盖箱子50个.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
