《8.3平行线的特征》[下学期]

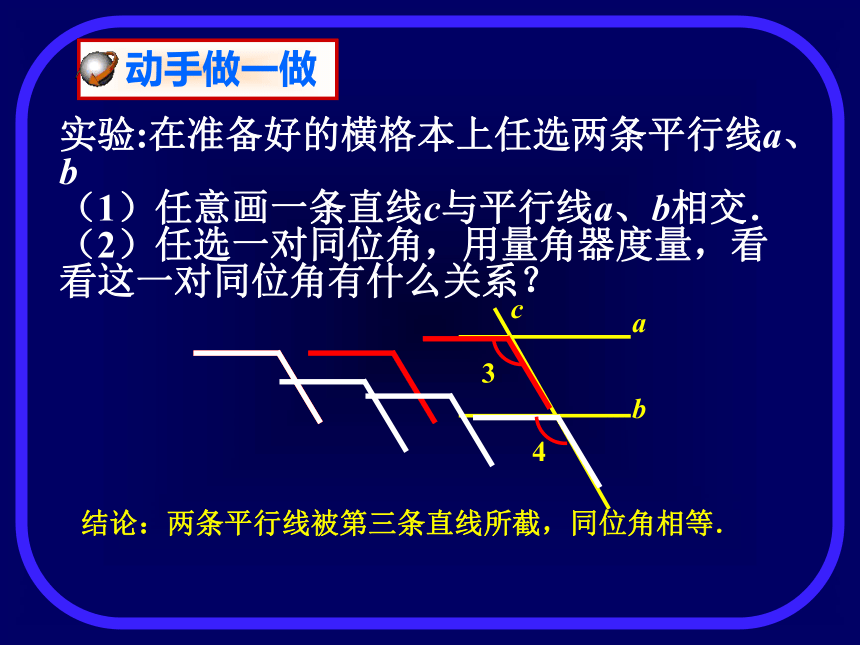
课件13张PPT。8.3 平行线的特征 实验:在准备好的横格本上任选两条平行线a、b
（1）任意画一条直线c与平行线a、b相交．
（2）任选一对同位角，用量角器度量，看看这一对同位角有什么关系？结论：两条平行线被第三条直线所截，同位角相等．
简单说成：两直线平行，同位角相等．1、平行线的特征1：
两条平行线被第三条直线所截，同位角相等． 思考回答下列问题：
（1）平行线的特征（1）已知的什么？得出的结论是什么？
（2）它和我们前面学习的两直线平行的条件（判定） “同位角相等，两直线平行”有什么区别？∵ AB//CD ( 已知 )∴∠1=∠2 （ ）两直线平行，同位角相等
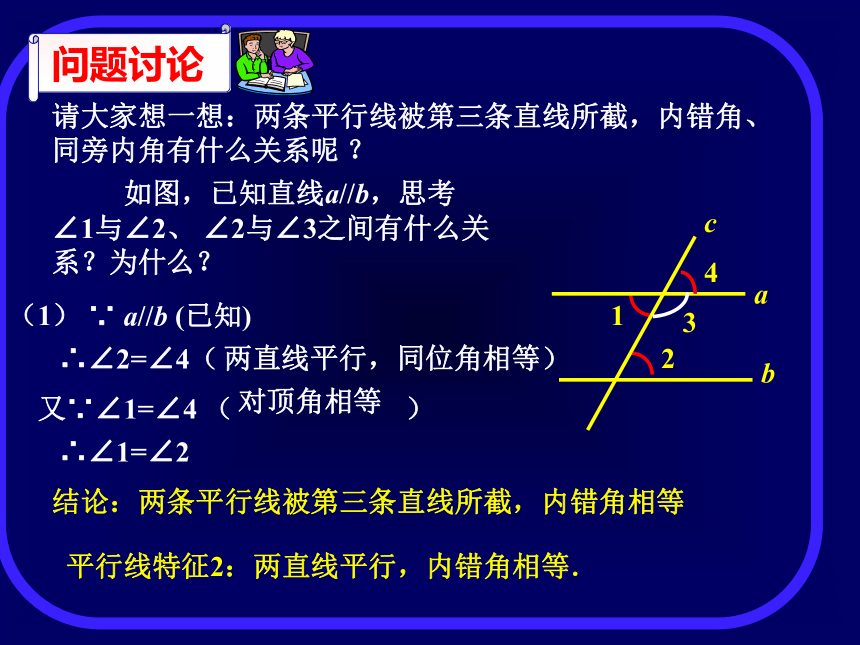
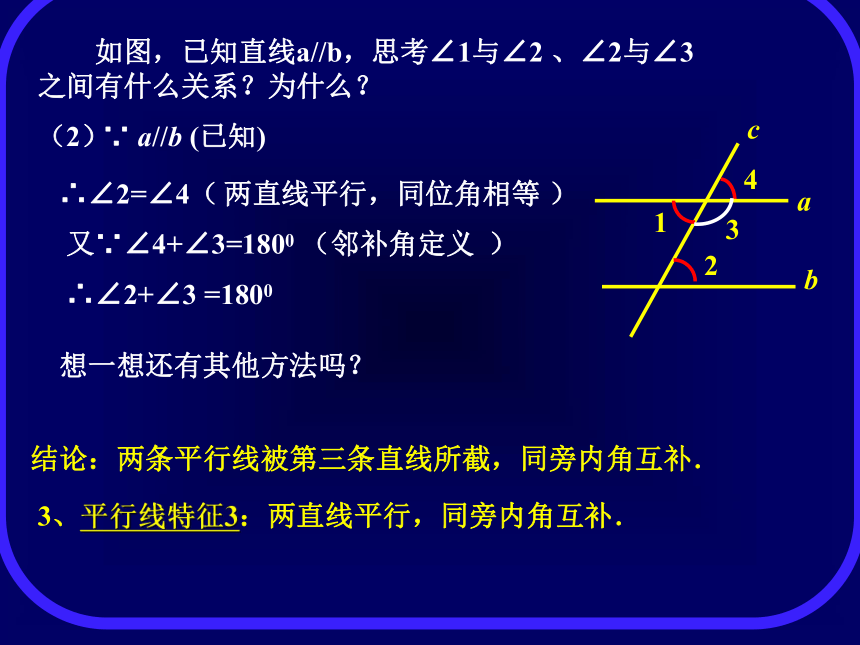
请大家想一想：两条平行线被第三条直线所截，内错角、同旁内角有什么关系呢 ？ 如图，已知直线a//b，思考∠1与∠2、 ∠2与∠3之间有什么关系？为什么？ （1）∵ a//b (已知)∴∠2=∠4（ ）两直线平行，同位角相等又∵∠1=∠4 （ ）对顶角相等∴∠1=∠2结论：两条平行线被第三条直线所截，内错角相等平行线特征2：两直线平行，内错角相等． 如图，已知直线a//b，思考∠1与∠2 、∠2与∠3之间有什么关系？为什么？ ∵ a//b (已知)∴∠2=∠4（ ）又∵∠4+∠3=1800 （ ）∴∠2+∠3 =1800 3、平行线特征3：两直线平行，同旁内角互补．（2）两直线平行，同位角相等邻补角定义结论：两条平行线被第三条直线所截，同旁内角互补．想一想还有其他方法吗？思考回答下列问题：
（1）平行线特征2、3已知的什么？得出的结论是什么？
（2）它和我们前面学习的两直线平行的条件：“内错角相等，两直线平行”；“同旁内角互补，两直线平行”有什么区别？ ∠3+∠2 =1800 （
）两直线平行，同旁内角互补∵ AB//CD ( 已知 )∴∠1=∠2 （ ）两直线平行，内错角相等2、平行线特征2：两直线平行，内错角相等．3、平行线特征3：两直线平行，同旁内角互补．平行线的三个特征：两直线平行同位角相等内错角相等同旁内角互补两直线平行的三个条件：两直线平行同位角相等内错角相等同旁内角互补例1：小青不小心把家里的梯形玻璃块打碎了，还剩下梯
形上底的一部分（如图）．要订造一块新的玻璃，已经
量得 ∠A=1150，∠D=1000． 你想一想，梯形另外两个角
各是多少度？(已知梯形的两底AD//BC)
解:∵ AD//BC （已知）.∴ ∠A＋∠B＝1800；∠C＋∠D＝1800（两直线平行，同旁内角互补）.又∵ ∠A=1150；∠D=1000. (已知)∴ ∠B＝1800－∠A＝1800－1150＝650.
∠C＝1800－∠D＝1800－1000＝800.1、如图，一条公路两次拐弯后，和原来的方向相同，也就是拐弯前后的两条路互相平行．第一次拐的角∠B等于1420，第二次拐的角∠C是多少度？为什么？2、如图，直线DE经过点A，DE//BC，∠B=440，∠C=570．
（1）∠DAB 等于多少度？为什么？
（2）∠DAC 等于多少度？为什么？1420？∴ ∠1= ∠ 2（ ）. 例2 如图，AD//BC,AB//DC , ∠1=100o,求∠ 2， ∠ 3的度数．解：∵ AD//BC（已知）.∴ ∠2= 100o.两直线平行,内错角相等∵ ∠1=100o（已知）∵ AB//CD∴ ∠1 ＋∠ 3＝180o（ ）两直线平行，同旁内角互补
∴ ∠ 3 ＝180o－∠1＝80o课堂小结1、平行线的三个特征：2、平行线的特征与平行线的判定的区别． 家庭作业: 教材第50页，1、3题；第55页，10、11、13题．两直线平行，同位角相等．两直线平行，内错角相等．两直线平行，同旁内角互补．判定：特征：3、证平行，用判定．知平行，用特征角的关系平行的关系角的关系平行的关系∴ DE//BC（ ）.注意：此处应用的是平行线的判定．练习：已知：如图，∠ADE=600，∠B=600，∠C=800．
问∠ AED等于多少度？为什么？解：∵ ∠ADE=∠B=600 （已知）∴ ∠AED=∠C=800 ( ).注意：此处应用的是平行线的性质．同位角相等，两直线平行两直线平行，同位角相等再见