《10.3同底数幂的除法》课件[下学期]
文档属性
| 名称 | 《10.3同底数幂的除法》课件[下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 245.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-16 00:00:00 | ||
图片预览

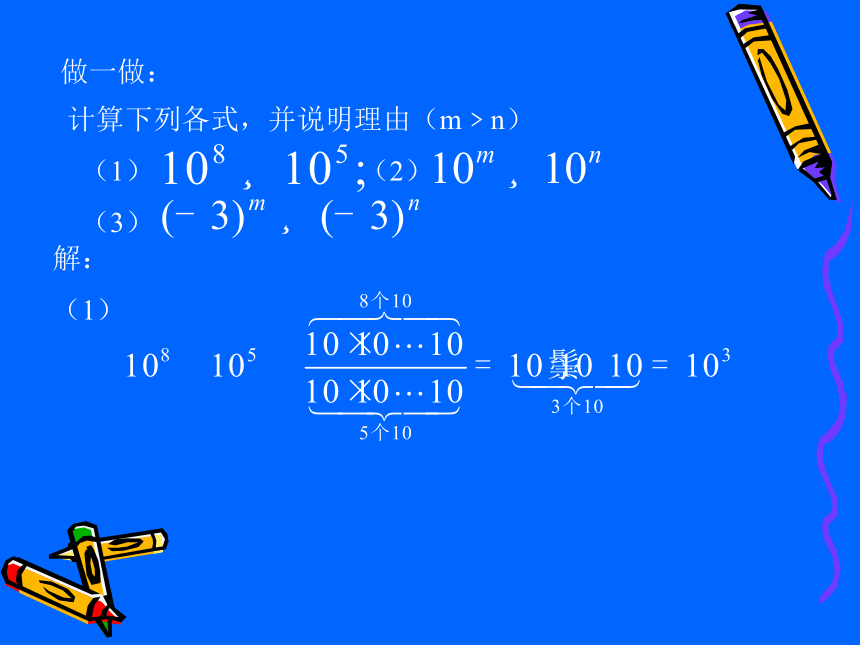


文档简介
课件13张PPT。10.3 同底数幂的
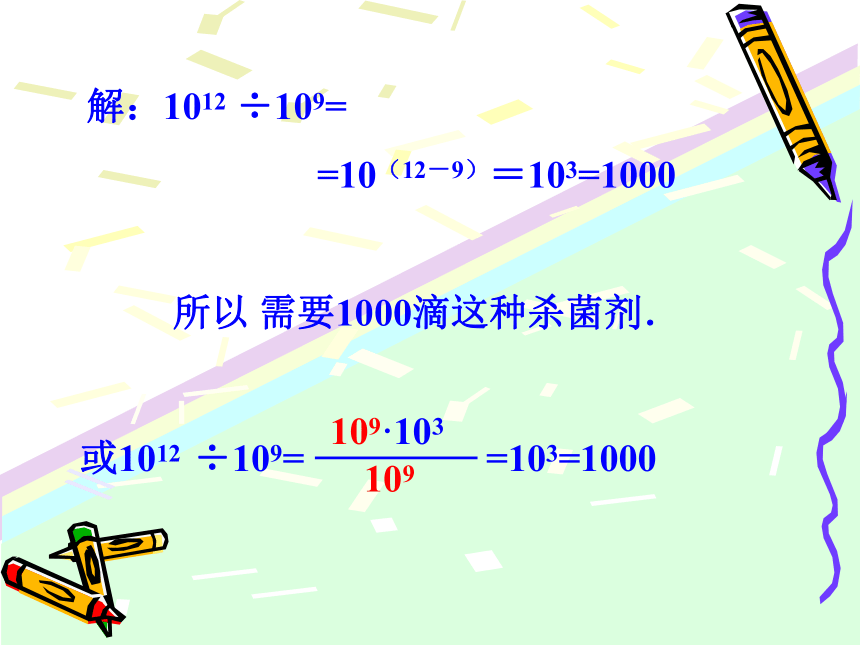
除法一种液体每升含有 个有害细菌,为了试验某种杀 菌剂的效果,科学家进行了实验,发现1滴杀菌剂可以杀死 个此种细菌,要将1升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?你是怎样计算的?解:1012 ÷109=
=10(12-9)=103=1000
所以 需要1000滴这种杀菌剂. 或1012 ÷109= =103=1000计算下列各式,并说明理由(m﹥n)
(1) (2)
(3) 做一做:解:
(1)同底数幂相除 ,底数不变,指数相减
am ÷an = a m-n (a≠0,m、n都是正整数,且 m>n)
am ÷an = = = a m-n 说明:底数 a 可以是字母、数字、单项式或多项式 (m-n)个a[例1] 计算:(1)(2)(3)(4)(5)(6) (7)地震的强度通常用里克特震级表示,描绘地震级数字表示地震的强度是 10 的若干次幂.例如,用里可特震级表示地震是8级,说明地震的强度是 .1992年4月,荷兰发生了5级地震,12天后,加利福尼亚发生了7级地震,加利福尼亚的地震强度是荷兰地震强度的多少倍?解:(2)(3)(4)(5)(6)所以,加利福尼亚的地震强度是荷兰地震强度的100倍.练一练(1) .1. 37 ÷ 34 2.3. (ab)10÷(ab)8 4. (y8)2 ÷y8想一想:
10000=104 , 16=24
1000=10(), 8=2()
100=10() , 4=2()
10=10(), 2=2()
猜一猜:
1=10() 1=2()
0.1=10() =2()
0.01=10() =2()
0.001=10() =2()由猜一猜发现: 10 0 =1 20 =1
10-1= 0.1= 2-1 =
10-2= 0.01= 2-2=
10-3= 0.001= 2-3=规定:a0 =1,(a≠0),a-p=
( a≠0 ,且 p为正整数)[例 3]用小数或分数分别表示下列各数:解:课时小结1.我们知道了指数有正整数,还有负整数、零 .
a0 =1,(a≠0),
a-p= ( a≠0 ,且 p为正整数)2.同底数幂的除法法则
am ÷an = a m-n (a≠0,m、n都是正整数,且m>n)中的条件可以改为:
(a≠0,m、n都是正整数)布置作业P95页 2、3、4.
=10(12-9)=103=1000
所以 需要1000滴这种杀菌剂. 或1012 ÷109= =103=1000计算下列各式,并说明理由(m﹥n)
(1) (2)
(3) 做一做:解:
(1)同底数幂相除 ,底数不变,指数相减
am ÷an = a m-n (a≠0,m、n都是正整数,且 m>n)
am ÷an = = = a m-n 说明:底数 a 可以是字母、数字、单项式或多项式 (m-n)个a[例1] 计算:(1)(2)(3)(4)(5)(6) (7)地震的强度通常用里克特震级表示,描绘地震级数字表示地震的强度是 10 的若干次幂.例如,用里可特震级表示地震是8级,说明地震的强度是 .1992年4月,荷兰发生了5级地震,12天后,加利福尼亚发生了7级地震,加利福尼亚的地震强度是荷兰地震强度的多少倍?解:(2)(3)(4)(5)(6)所以,加利福尼亚的地震强度是荷兰地震强度的100倍.练一练(1) .1. 37 ÷ 34 2.3. (ab)10÷(ab)8 4. (y8)2 ÷y8想一想:
10000=104 , 16=24
1000=10(), 8=2()
100=10() , 4=2()
10=10(), 2=2()
猜一猜:
1=10() 1=2()
0.1=10() =2()
0.01=10() =2()
0.001=10() =2()由猜一猜发现: 10 0 =1 20 =1
10-1= 0.1= 2-1 =
10-2= 0.01= 2-2=
10-3= 0.001= 2-3=规定:a0 =1,(a≠0),a-p=
( a≠0 ,且 p为正整数)[例 3]用小数或分数分别表示下列各数:解:课时小结1.我们知道了指数有正整数,还有负整数、零 .
a0 =1,(a≠0),
a-p= ( a≠0 ,且 p为正整数)2.同底数幂的除法法则
am ÷an = a m-n (a≠0,m、n都是正整数,且m>n)中的条件可以改为:
(a≠0,m、n都是正整数)布置作业P95页 2、3、4.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
