平行四边形的性质[下学期]
文档属性
| 名称 | 平行四边形的性质[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 291.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-19 17:54:00 | ||
图片预览




文档简介
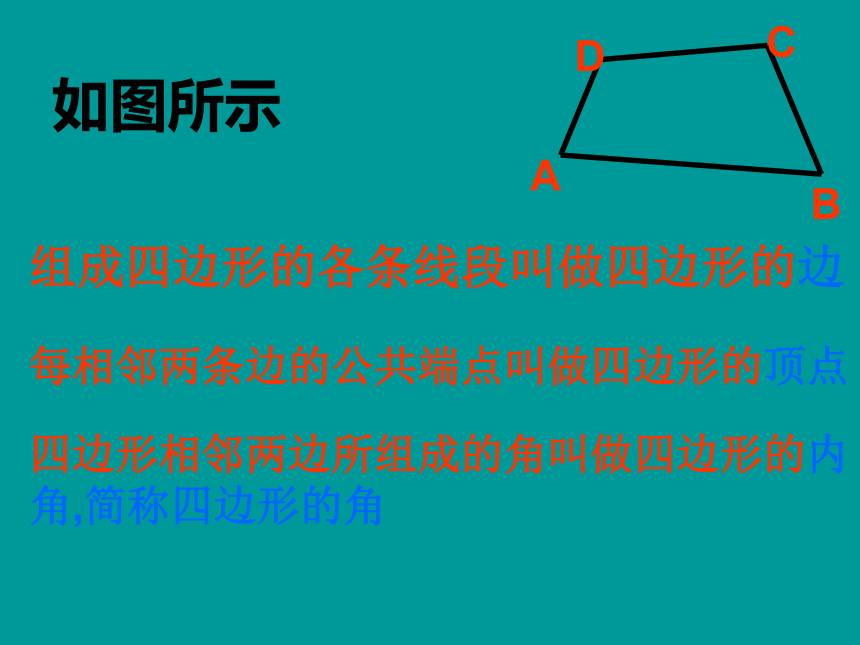
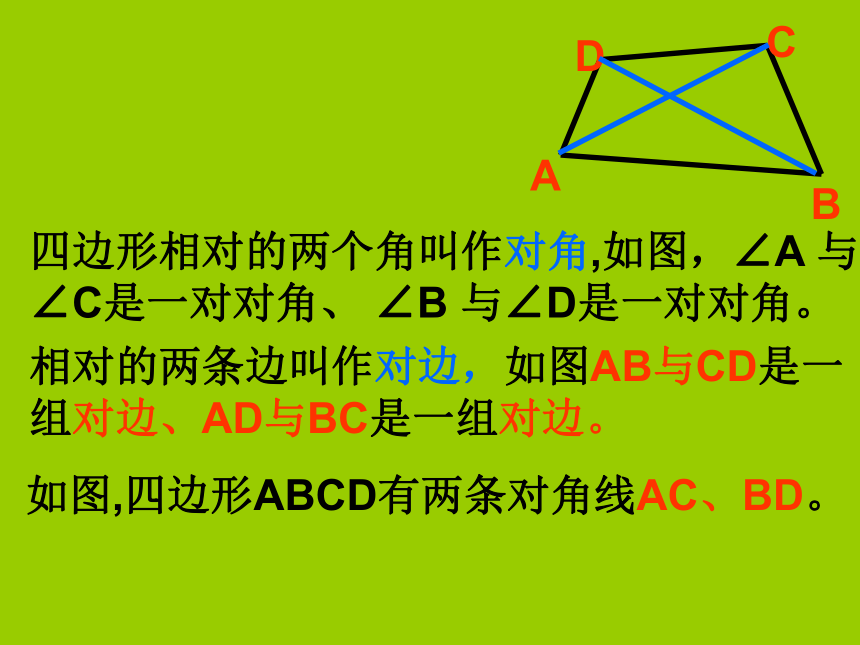
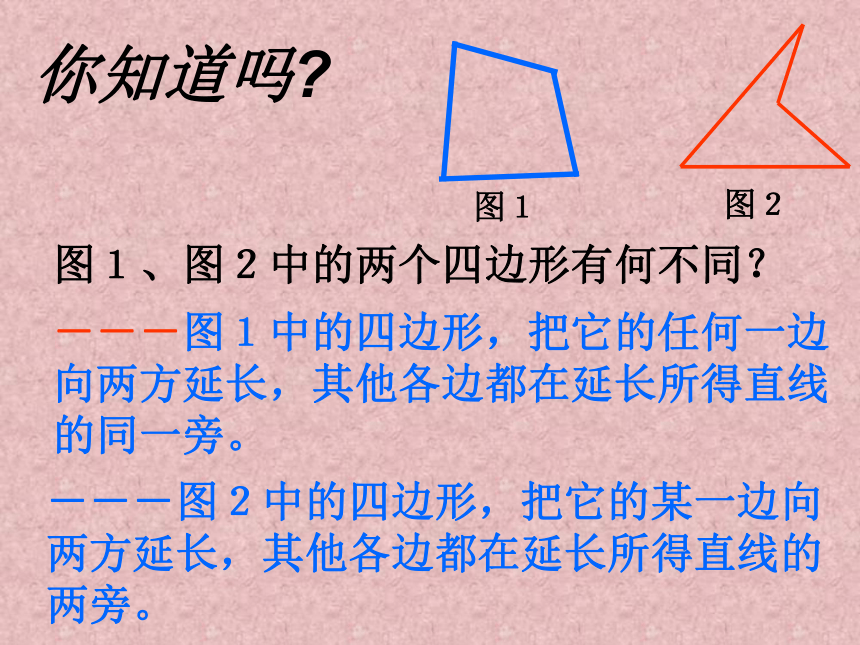
课件18张PPT。平行四边形的性质各式各样的图案,装点着我们的生活欣赏思考(1) 这些物体的形状有什么共同特点?(2)四边形有什么共同特点?(3)你能给四边形下一个确切的定义吗?如图所示组成四边形的各条线段叫做四边形的边每相邻两条边的公共端点叫做四边形的顶点四边形相邻两边所组成的角叫做四边形的内角,简称四边形的角如图,四边形ABCD有两条对角线AC、BD。四边形相对的两个角叫作对角,如图,∠A 与∠C是一对对角、 ∠B 与∠D是一对对角。相对的两条边叫作对边,如图AB与CD是一组对边、AD与BC是一组对边。图1、图2中的两个四边形有何不同?---图1中的四边形,把它的任何一边向两方延长,其他各边都在延长所得直线的同一旁。---图2中的四边形,把它的某一边向两方延长,其他各边都在延长所得直线的两旁。你知道吗?请同学们将准备好的两个全等的三角形纸片,把它们相等的一组边重合,得到一个四边形.1.你拼出了怎样的四边形,和同学互相交流一下.2.这个四边形的相对的边(即对边)有怎样的位置关系?说说你的理由.因为△ABD≌△CDB所以∠1=∠2
∠3=∠4这个四边形的两组对边分别平行.2.这个四边形的对边有怎样的位置关系?说说你的理由.
答:这个四边形的对边分别平行,理由是:内错角相等两直线平行AD∥BC
AB∥CD
定义:两组对边分别平行的四边形叫做平行四边形. 如图所示的四边形ABCD,是平行四边形记作: ABCD读作:平行四边形ABCD四边形平行四边形两组对边分别平行定义可简单地说成:∵ 四边形ABCD是平行四边形
∴ AB∥CD
AD∥BC在四边形ABCD中
∵ AB∥DC,AD∥BC
∴ 四边形ABCD是平行四边形 推理过程:正向反向学以致用认真观察图形的运动过程后、思考并回答问题.1.∠A经过平移后与哪个角重合, ∠B呢?2.AB边经过平移后与哪条边重合,BC边呢? ∠ A与∠ C重合, ∠ B与 ∠ D重合3.那么平行四边形ABCD相对的边(简称对边),相对的角(简称对角)分别有什么关系呢?平行四边形的对边相等
平行四边形的对角相等平行四边形能用别的方法验证你的结论吗?∠A=∠C
∠1=∠2
∠4=∠3对边相等对角相等思考:平行四边形的邻角有 什么关系?平行四边形
的性质平行四边形的邻角互补平行四边形的对边相等
平行四边形的对角相等动脑筋如图l1∥l2,
AB∥CD那么AB与CD相等?为什么?结论:夹在两条平行线间的平行线段相等1、四边形ABCD是平行四边形,则∠ADC= , ∠BCD= 。
AB= ,BC= 。56°124°2530(1题图)2 、四边形ABCD是平行四边形,它的四条边中哪
些线段可以通过平移相互得到?随堂练习答:对边可以通过平移相互得到,平移的距离等于另一组对边的长3、课本72页练习第1、2题感悟与收获通过本节课的学习,你有什么收获?平行四边形的邻角互补
2、平行四边形的性质:1 、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形平行四边形的对边相等
平行四边形的对角相等
∠3=∠4这个四边形的两组对边分别平行.2.这个四边形的对边有怎样的位置关系?说说你的理由.
答:这个四边形的对边分别平行,理由是:内错角相等两直线平行AD∥BC
AB∥CD
定义:两组对边分别平行的四边形叫做平行四边形. 如图所示的四边形ABCD,是平行四边形记作: ABCD读作:平行四边形ABCD四边形平行四边形两组对边分别平行定义可简单地说成:∵ 四边形ABCD是平行四边形
∴ AB∥CD
AD∥BC在四边形ABCD中
∵ AB∥DC,AD∥BC
∴ 四边形ABCD是平行四边形 推理过程:正向反向学以致用认真观察图形的运动过程后、思考并回答问题.1.∠A经过平移后与哪个角重合, ∠B呢?2.AB边经过平移后与哪条边重合,BC边呢? ∠ A与∠ C重合, ∠ B与 ∠ D重合3.那么平行四边形ABCD相对的边(简称对边),相对的角(简称对角)分别有什么关系呢?平行四边形的对边相等
平行四边形的对角相等平行四边形能用别的方法验证你的结论吗?∠A=∠C
∠1=∠2
∠4=∠3对边相等对角相等思考:平行四边形的邻角有 什么关系?平行四边形
的性质平行四边形的邻角互补平行四边形的对边相等
平行四边形的对角相等动脑筋如图l1∥l2,
AB∥CD那么AB与CD相等?为什么?结论:夹在两条平行线间的平行线段相等1、四边形ABCD是平行四边形,则∠ADC= , ∠BCD= 。
AB= ,BC= 。56°124°2530(1题图)2 、四边形ABCD是平行四边形,它的四条边中哪
些线段可以通过平移相互得到?随堂练习答:对边可以通过平移相互得到,平移的距离等于另一组对边的长3、课本72页练习第1、2题感悟与收获通过本节课的学习,你有什么收获?平行四边形的邻角互补
2、平行四边形的性质:1 、平行四边形的定义:两组对边分别平行的四边形叫做平行四边形平行四边形的对边相等
平行四边形的对角相等
