人教版2023年九年级上册 第21章 一元二次方程 单元检测卷(含解析)
文档属性
| 名称 | 人教版2023年九年级上册 第21章 一元二次方程 单元检测卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 146.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览



文档简介
人教版2023年九年级上册 第21章 一元二次方程 单元检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列关于x的方程是一元二次方程的是( )
A.x﹣1=3(x﹣2) B.+x2=0 C.a2x+c=0 D.x2﹣2x=0
2.关于x的一元二次方程x2=5x﹣1的二次项系数、一次项系数、常数项分别是( )
A.1,﹣5,﹣1 B.﹣1,﹣5,﹣1 C.1,﹣5,1 D.1,5,1
3.一元二次方程x2﹣8x﹣1=0配方后可变形为( )
A.(x﹣4)2=3 B.(x﹣4)2=15 C.(x﹣4)2=17 D.(x+4)2=17
4.已知m是方程x2﹣3x﹣1=0的一个根,则代数式2m2﹣6m的值为( )
A.0 B.2 C.﹣2 D.4
5.一元二次方程x2﹣4x+3=0的解是( )
A.x1=3,x2=1 B.x1=﹣3,x2=1
C.x1=3,x2=﹣1 D.x1=﹣3,x2=﹣1
6.用公式法解方程3x2+4=12x,下列代入公式正确的是( )
A.x= B.x=
C.x= D.x=
7.一元二次方程x2+2x+1=0的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
8.某商品原价为100元,连续两次降价后为80元,设平均每次降价的百分率为x,则下列方程正确的是( )
A.80(1﹣x)2=100 B.100(1﹣x)2=80
C.100(1﹣2x)2=80 D.80(1﹣2x)2=100
9.“新冠肺炎”防治取得战略性成果.若有一个人患了“新冠肺炎”,经过两轮传染后共有16个人患了“新冠肺炎”,则每轮传染中平均一个人传染的人数是( )
A.2 B.3 C.4 D.5
10.已知(a2+b2)(a2+b2﹣2)=3,则a2+b2的值为( )
A.3 B.﹣1 C.﹣3或1 D.3或﹣1
二.填空题(共6小题,满分18分,每小题3分)
11.若方程(m+3)+mx﹣2=0是关于x的一元二次方程,则m等于 .
12.已知关于x的一元二次方程x2+x﹣k=0的一个根是1,则k的值是 .
13.方程x2﹣x=0解为 .
14.某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,设航空公司共有x个飞机场,列方程 .
15.若菱形两条对角线的长度是方程x2﹣9x+20=0的两根,则该菱形的面积为 .
16.设关于x的方程x2﹣2x﹣m+1=0的两个实数根分别为α,β,若|α|+|β|=6,那么实数m的取值是 .
三.解答题(共6小题,满分52分)
17.(8分)解方程:
(1)x(x+1)=x+1;
(2)2x2﹣4x+1=0.
18.(8分)已知关于x的一元二次方程x2﹣4mx+3m2=0.
(1)当m=﹣1时,请求出方程的解;
(2)试说明方程总有两个实数根.
19.(8分)手工课上,小明同学准备用铁丝围成一个长方形,长方形的长与宽的比是3:2,长方形的面积是30dm2.
(1)求长方形的长和宽分别是多少;
(2)小明现有一根长为23dm的铁丝,能否围成符合上述要求的长方形?请说明理由.
20.(9分)阅读材料,解答问题.
解方程:(4x﹣1)2﹣10(4x﹣1)+24=0.
解:把4x﹣1视为一个整体,设4x﹣1=y,
则原方程可化为y2﹣10y+24=0.
解得y1=6,y2=4.
∴4x﹣1=6或4x﹣1=4.
∴.
以上方法就叫换元法,达到简化或降次的目的,体现了转化的思想.
请仿照材料解下列方程:
(1)(3x﹣5)2+4(3x﹣5)+3=0;
(2)x4﹣x2﹣6=0.
21.(9分)某商场服装部销售一种名牌衬衫,平均每天可售出30件,每件盈利40元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价3元时,平均每天可多卖出6件.
(1)设降价x元,则现在每天可销售衬衫 件,每件的利润是 元.(用x的代数式表示)
(2)若商场要求该服装部每天盈利1400元,问每件要降价多少元?
(3)若商场要求该服装部每天盈利1600元,问这个要求能否实现?请说说你的理由.
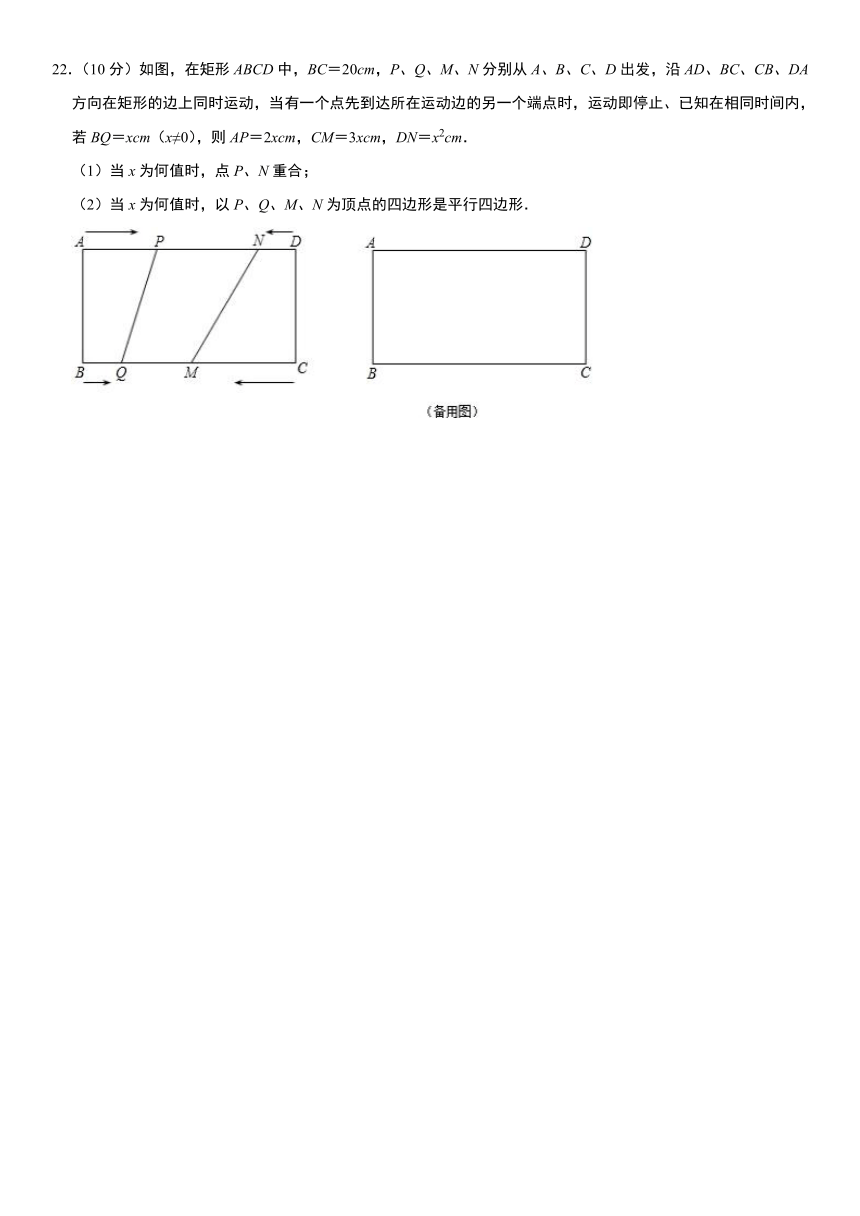
22.(10分)如图,在矩形ABCD中,BC=20cm,P、Q、M、N分别从A、B、C、D出发,沿AD、BC、CB、DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止、已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.
(1)当x为何值时,点P、N重合;
(2)当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:A.方程是一元一次方程,方程不是一元二次方程,故本选项不符合题意;
B.方程是分式方程,不是整式方程,方程不是一元二次方程,故本选项不符合题意;
C.当a≠0时,方程是一元一次方程,方程不是一元二次方程,故本选项不符合题意;
D.方程是一元二次方程,故本选项符合题意;
故选:D.
2.【解答】解:由原方程得到:x2﹣5x+1=0,则该方程的二次项系数、一次项系数、常数项分别是1,﹣5,1.
故选:C.
3.【解答】解:x2﹣8x﹣1=0变形为:x2﹣8x=1,
配方得:x2﹣8x+16=17,
即(x﹣4)2=17;
故选:C.
4.【解答】解:∵m是方程x2﹣3x﹣1=0的一个根,
∴m2﹣3m﹣1=0,
∴m2﹣3m=1,
∴2m2﹣6m=2(m2﹣3m)=2×1=2,
故选:B.
5.【解答】解:x2﹣4x+3=0,
(x﹣3)(x﹣1)=0,
∴x﹣3=0或x﹣1=0,
∴x1=3,x2=1.
故选:A.
6.【解答】解:3x2+4=12x,
3x2﹣12x+4=0,
这里a=3,b=﹣12,c=4,
b2﹣4ac=(﹣12)2﹣4×3×4,
x===,
故选:D.
7.【解答】解:由题意可知:Δ=22﹣4×1×1=0,
∴方程有两个相等的实数根.
故选:B.
8.【解答】解:由题意得:100(1﹣x)2=80,
故选:B.
9.【解答】解:设每轮传染中平均一个人传染了x个人,
根据题意,得1+x+(x+1)x=16,
x=3或x=﹣5(舍去).
答:每轮传染中平均一个人传染了3个人.
故选:B.
10.【解答】解:设a2+b2=m,
则原式为m(m﹣2)=3,
整理得:m2﹣2m﹣3=0,
因式分解得:(m﹣3)(m+1)=0,
∴m=3或m=﹣1,
∵a2+b2≥0,
∴a2+b2的值为3,
故选:A.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:∵方程(m+3)+mx﹣2=0是关于x的一元二次方程,
∴,
解得m=3.
故答案为:3.
12.【解答】解:由题意得:把x=1代入方程x2+x﹣k=0中得:
12+1﹣k=0,
解得:k=2,
故答案为:2.
13.【解答】解:x2﹣x=0,
x(x﹣1)=0,
x=0或x﹣1=0,
所以x1=0,x2=1.
故答案为:x1=0,x2=1.
14.【解答】解:设共有x个飞机场.
x(x﹣1)=10.
故答案为:x(x﹣1)=10.
15.【解答】解:解方程x2﹣9x+20=0得到x=4或5,
∴菱形的对角线长分别为4和5,
∴菱形的面积=×4×5=10,
故答案为:10.
16.【解答】解:∵关于x的方程x2﹣2x﹣m+1=0的两个实数根分别为α,β,
∴α+β=2,αβ=﹣m+1,
∵|α|+|β|=6,
∴α,β为异号,
即αβ<0,
由α+β=2得α2+β2=4﹣2αβ,
由|α|+|β|=6得α2+β2=36﹣2|αβ|,
∴4﹣2αβ=36﹣2|αβ|=36+2αβ,
∴αβ=﹣8,
∴﹣m+1=﹣8,
∴m=9,
故答案为:9.
三.解答题(共6小题,满分52分)
17.【解答】解:(1)x(x+1)=x+1,
x(x+1)﹣(x+1)=0,
(x+1)(x﹣1)=0,
x+1=0或x﹣1=0,
所以x1=﹣1,x2=1;
(2)2x2﹣4x+1=0,
x2﹣2x=﹣,
x2﹣2x+1=﹣+1,
(x﹣1)2=,
x﹣1=±,
所以x1=1+,x2=1﹣.
18.【解答】(1)解:当m=﹣1时,原方程化为x2+4x+3=0,
∴(x+1)(x+3)=0,
∴x+1=0或x+3=0,
∴x1=﹣1,x2=﹣3;
(2)证明:∵x2﹣4mx+3m2=0中,a=1,b=﹣4m,c=3m2,
∴Δ=b2﹣4ac=(﹣4m)2﹣4×1×3m2=4m2,
∵4m2≥0,即Δ≥0,
∴原方程总有两个实数根.
19.【解答】解:(1)设长方形的长为3xdm,则宽为2xdm,
根据题意得:3x 2x=30,
解得:x1=,x2=﹣(不符合题意,舍去),
∴3x=3×=3,2x=2×=2.
答:长方形的长为3dm,宽为2dm;
(2)能否围成符合上述要求的长方形,理由如下:
(3+2)×2
=5×2
=10(dm),
∵10≈22.36<23,
∴能围成符合上述要求的长方形.
20.【解答】解:(1)设3x﹣5=y,则原方程可化为y2+4y+3=0,
整理,得(y+3)(y+1)=0,
解得y1=﹣3,y2=﹣1.
当y=﹣3时,即3x﹣5=﹣3,
解得x1=,
当y=﹣1时,即3x﹣5=﹣1,
解得x2=.
综上所述,原方程的解为x1=,x2=;
(2)设x2=y,则原方程可化为y2﹣y﹣6=0,
整理,得(y﹣3)(y+2)=0,
解得y1=3,y2=﹣2.
当y=3时,即x2=3,
∴x=±,
当y=﹣2时,x2=﹣2无解.
∴原方程的解为x1=,x2=﹣.
21.【解答】解:(1)设降价x元,则现在每天可销售衬衫(30+2x)件,每件的利润是(40﹣x)元;
(2)由题意,得(40﹣x)(30+2x)=1400,
即:(x﹣5)(x﹣20)=0,
解得x1=5,x2=20,
为了扩大销售量,减少库存,所以x的值应为20,
所以,若商场要求该服装部每天盈利1400元,每件要降价20元;
(3)假设能达到,由题意,得(40﹣x)(30+2x)=1600,
整理,得x2﹣25x+200=0,
△=252﹣4×1×200=625﹣800=﹣175<0,
即:该方程无解,
所以,商场要求该服装部每天盈利1600元,这个要求不能实现.
故答案为:(30+2x),(40﹣x).
22.【解答】解:(1)∵P,N重合,
∴2x+x2=20,
∴,(舍去),
∴当时,P,N重合;
(2)因为当N点到达A点时,x=2,此时M点和Q点还未相遇,
所以点Q只能在点M的左侧,
①当点P在点N的左侧时,依题意得
20﹣(x+3x)=20﹣(2x+x2),
解得x1=0(舍去),x2=2,
当x=2时四边形PQMN是平行四边形;
②当点P在点N的右侧时,依题意得
20﹣(x+3x)=(2x+x2)﹣20,
解得x1=﹣10(舍去),x2=4,
当x=4时四边形NQMP是平行四边形,
所以当x=2或x=4时,以P,Q,M,N为顶点的四边形是平行四边形.
一.选择题(共10小题,满分30分,每小题3分)
1.下列关于x的方程是一元二次方程的是( )
A.x﹣1=3(x﹣2) B.+x2=0 C.a2x+c=0 D.x2﹣2x=0
2.关于x的一元二次方程x2=5x﹣1的二次项系数、一次项系数、常数项分别是( )
A.1,﹣5,﹣1 B.﹣1,﹣5,﹣1 C.1,﹣5,1 D.1,5,1
3.一元二次方程x2﹣8x﹣1=0配方后可变形为( )
A.(x﹣4)2=3 B.(x﹣4)2=15 C.(x﹣4)2=17 D.(x+4)2=17
4.已知m是方程x2﹣3x﹣1=0的一个根,则代数式2m2﹣6m的值为( )
A.0 B.2 C.﹣2 D.4
5.一元二次方程x2﹣4x+3=0的解是( )
A.x1=3,x2=1 B.x1=﹣3,x2=1
C.x1=3,x2=﹣1 D.x1=﹣3,x2=﹣1
6.用公式法解方程3x2+4=12x,下列代入公式正确的是( )
A.x= B.x=
C.x= D.x=
7.一元二次方程x2+2x+1=0的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
8.某商品原价为100元,连续两次降价后为80元,设平均每次降价的百分率为x,则下列方程正确的是( )
A.80(1﹣x)2=100 B.100(1﹣x)2=80
C.100(1﹣2x)2=80 D.80(1﹣2x)2=100
9.“新冠肺炎”防治取得战略性成果.若有一个人患了“新冠肺炎”,经过两轮传染后共有16个人患了“新冠肺炎”,则每轮传染中平均一个人传染的人数是( )
A.2 B.3 C.4 D.5
10.已知(a2+b2)(a2+b2﹣2)=3,则a2+b2的值为( )
A.3 B.﹣1 C.﹣3或1 D.3或﹣1
二.填空题(共6小题,满分18分,每小题3分)
11.若方程(m+3)+mx﹣2=0是关于x的一元二次方程,则m等于 .
12.已知关于x的一元二次方程x2+x﹣k=0的一个根是1,则k的值是 .
13.方程x2﹣x=0解为 .
14.某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,设航空公司共有x个飞机场,列方程 .
15.若菱形两条对角线的长度是方程x2﹣9x+20=0的两根,则该菱形的面积为 .
16.设关于x的方程x2﹣2x﹣m+1=0的两个实数根分别为α,β,若|α|+|β|=6,那么实数m的取值是 .
三.解答题(共6小题,满分52分)
17.(8分)解方程:
(1)x(x+1)=x+1;
(2)2x2﹣4x+1=0.
18.(8分)已知关于x的一元二次方程x2﹣4mx+3m2=0.
(1)当m=﹣1时,请求出方程的解;
(2)试说明方程总有两个实数根.
19.(8分)手工课上,小明同学准备用铁丝围成一个长方形,长方形的长与宽的比是3:2,长方形的面积是30dm2.
(1)求长方形的长和宽分别是多少;
(2)小明现有一根长为23dm的铁丝,能否围成符合上述要求的长方形?请说明理由.
20.(9分)阅读材料,解答问题.
解方程:(4x﹣1)2﹣10(4x﹣1)+24=0.
解:把4x﹣1视为一个整体,设4x﹣1=y,
则原方程可化为y2﹣10y+24=0.
解得y1=6,y2=4.
∴4x﹣1=6或4x﹣1=4.
∴.
以上方法就叫换元法,达到简化或降次的目的,体现了转化的思想.
请仿照材料解下列方程:
(1)(3x﹣5)2+4(3x﹣5)+3=0;
(2)x4﹣x2﹣6=0.
21.(9分)某商场服装部销售一种名牌衬衫,平均每天可售出30件,每件盈利40元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价3元时,平均每天可多卖出6件.
(1)设降价x元,则现在每天可销售衬衫 件,每件的利润是 元.(用x的代数式表示)
(2)若商场要求该服装部每天盈利1400元,问每件要降价多少元?
(3)若商场要求该服装部每天盈利1600元,问这个要求能否实现?请说说你的理由.
22.(10分)如图,在矩形ABCD中,BC=20cm,P、Q、M、N分别从A、B、C、D出发,沿AD、BC、CB、DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止、已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.
(1)当x为何值时,点P、N重合;
(2)当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:A.方程是一元一次方程,方程不是一元二次方程,故本选项不符合题意;
B.方程是分式方程,不是整式方程,方程不是一元二次方程,故本选项不符合题意;
C.当a≠0时,方程是一元一次方程,方程不是一元二次方程,故本选项不符合题意;
D.方程是一元二次方程,故本选项符合题意;
故选:D.
2.【解答】解:由原方程得到:x2﹣5x+1=0,则该方程的二次项系数、一次项系数、常数项分别是1,﹣5,1.
故选:C.
3.【解答】解:x2﹣8x﹣1=0变形为:x2﹣8x=1,
配方得:x2﹣8x+16=17,
即(x﹣4)2=17;
故选:C.
4.【解答】解:∵m是方程x2﹣3x﹣1=0的一个根,
∴m2﹣3m﹣1=0,
∴m2﹣3m=1,
∴2m2﹣6m=2(m2﹣3m)=2×1=2,
故选:B.
5.【解答】解:x2﹣4x+3=0,
(x﹣3)(x﹣1)=0,
∴x﹣3=0或x﹣1=0,
∴x1=3,x2=1.
故选:A.
6.【解答】解:3x2+4=12x,
3x2﹣12x+4=0,
这里a=3,b=﹣12,c=4,
b2﹣4ac=(﹣12)2﹣4×3×4,
x===,
故选:D.
7.【解答】解:由题意可知:Δ=22﹣4×1×1=0,
∴方程有两个相等的实数根.
故选:B.
8.【解答】解:由题意得:100(1﹣x)2=80,
故选:B.
9.【解答】解:设每轮传染中平均一个人传染了x个人,
根据题意,得1+x+(x+1)x=16,
x=3或x=﹣5(舍去).
答:每轮传染中平均一个人传染了3个人.
故选:B.
10.【解答】解:设a2+b2=m,
则原式为m(m﹣2)=3,
整理得:m2﹣2m﹣3=0,
因式分解得:(m﹣3)(m+1)=0,
∴m=3或m=﹣1,
∵a2+b2≥0,
∴a2+b2的值为3,
故选:A.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:∵方程(m+3)+mx﹣2=0是关于x的一元二次方程,
∴,
解得m=3.
故答案为:3.
12.【解答】解:由题意得:把x=1代入方程x2+x﹣k=0中得:
12+1﹣k=0,
解得:k=2,
故答案为:2.
13.【解答】解:x2﹣x=0,
x(x﹣1)=0,
x=0或x﹣1=0,
所以x1=0,x2=1.
故答案为:x1=0,x2=1.
14.【解答】解:设共有x个飞机场.
x(x﹣1)=10.
故答案为:x(x﹣1)=10.
15.【解答】解:解方程x2﹣9x+20=0得到x=4或5,
∴菱形的对角线长分别为4和5,
∴菱形的面积=×4×5=10,
故答案为:10.
16.【解答】解:∵关于x的方程x2﹣2x﹣m+1=0的两个实数根分别为α,β,
∴α+β=2,αβ=﹣m+1,
∵|α|+|β|=6,
∴α,β为异号,
即αβ<0,
由α+β=2得α2+β2=4﹣2αβ,
由|α|+|β|=6得α2+β2=36﹣2|αβ|,
∴4﹣2αβ=36﹣2|αβ|=36+2αβ,
∴αβ=﹣8,
∴﹣m+1=﹣8,
∴m=9,
故答案为:9.
三.解答题(共6小题,满分52分)
17.【解答】解:(1)x(x+1)=x+1,
x(x+1)﹣(x+1)=0,
(x+1)(x﹣1)=0,
x+1=0或x﹣1=0,
所以x1=﹣1,x2=1;
(2)2x2﹣4x+1=0,
x2﹣2x=﹣,
x2﹣2x+1=﹣+1,
(x﹣1)2=,
x﹣1=±,
所以x1=1+,x2=1﹣.
18.【解答】(1)解:当m=﹣1时,原方程化为x2+4x+3=0,
∴(x+1)(x+3)=0,
∴x+1=0或x+3=0,
∴x1=﹣1,x2=﹣3;
(2)证明:∵x2﹣4mx+3m2=0中,a=1,b=﹣4m,c=3m2,
∴Δ=b2﹣4ac=(﹣4m)2﹣4×1×3m2=4m2,
∵4m2≥0,即Δ≥0,
∴原方程总有两个实数根.
19.【解答】解:(1)设长方形的长为3xdm,则宽为2xdm,
根据题意得:3x 2x=30,
解得:x1=,x2=﹣(不符合题意,舍去),
∴3x=3×=3,2x=2×=2.
答:长方形的长为3dm,宽为2dm;
(2)能否围成符合上述要求的长方形,理由如下:
(3+2)×2
=5×2
=10(dm),
∵10≈22.36<23,
∴能围成符合上述要求的长方形.
20.【解答】解:(1)设3x﹣5=y,则原方程可化为y2+4y+3=0,
整理,得(y+3)(y+1)=0,
解得y1=﹣3,y2=﹣1.
当y=﹣3时,即3x﹣5=﹣3,
解得x1=,
当y=﹣1时,即3x﹣5=﹣1,
解得x2=.
综上所述,原方程的解为x1=,x2=;
(2)设x2=y,则原方程可化为y2﹣y﹣6=0,
整理,得(y﹣3)(y+2)=0,
解得y1=3,y2=﹣2.
当y=3时,即x2=3,
∴x=±,
当y=﹣2时,x2=﹣2无解.
∴原方程的解为x1=,x2=﹣.
21.【解答】解:(1)设降价x元,则现在每天可销售衬衫(30+2x)件,每件的利润是(40﹣x)元;
(2)由题意,得(40﹣x)(30+2x)=1400,
即:(x﹣5)(x﹣20)=0,
解得x1=5,x2=20,
为了扩大销售量,减少库存,所以x的值应为20,
所以,若商场要求该服装部每天盈利1400元,每件要降价20元;
(3)假设能达到,由题意,得(40﹣x)(30+2x)=1600,
整理,得x2﹣25x+200=0,
△=252﹣4×1×200=625﹣800=﹣175<0,
即:该方程无解,
所以,商场要求该服装部每天盈利1600元,这个要求不能实现.
故答案为:(30+2x),(40﹣x).
22.【解答】解:(1)∵P,N重合,
∴2x+x2=20,
∴,(舍去),
∴当时,P,N重合;
(2)因为当N点到达A点时,x=2,此时M点和Q点还未相遇,
所以点Q只能在点M的左侧,
①当点P在点N的左侧时,依题意得
20﹣(x+3x)=20﹣(2x+x2),
解得x1=0(舍去),x2=2,
当x=2时四边形PQMN是平行四边形;
②当点P在点N的右侧时,依题意得
20﹣(x+3x)=(2x+x2)﹣20,
解得x1=﹣10(舍去),x2=4,
当x=4时四边形NQMP是平行四边形,
所以当x=2或x=4时,以P,Q,M,N为顶点的四边形是平行四边形.
同课章节目录
