4.1.2 点线面体同步练习题(含答案)
文档属性
| 名称 | 4.1.2 点线面体同步练习题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第四章 图形的初步认识
点、线、面、体
点、线、面、体及之间的联系
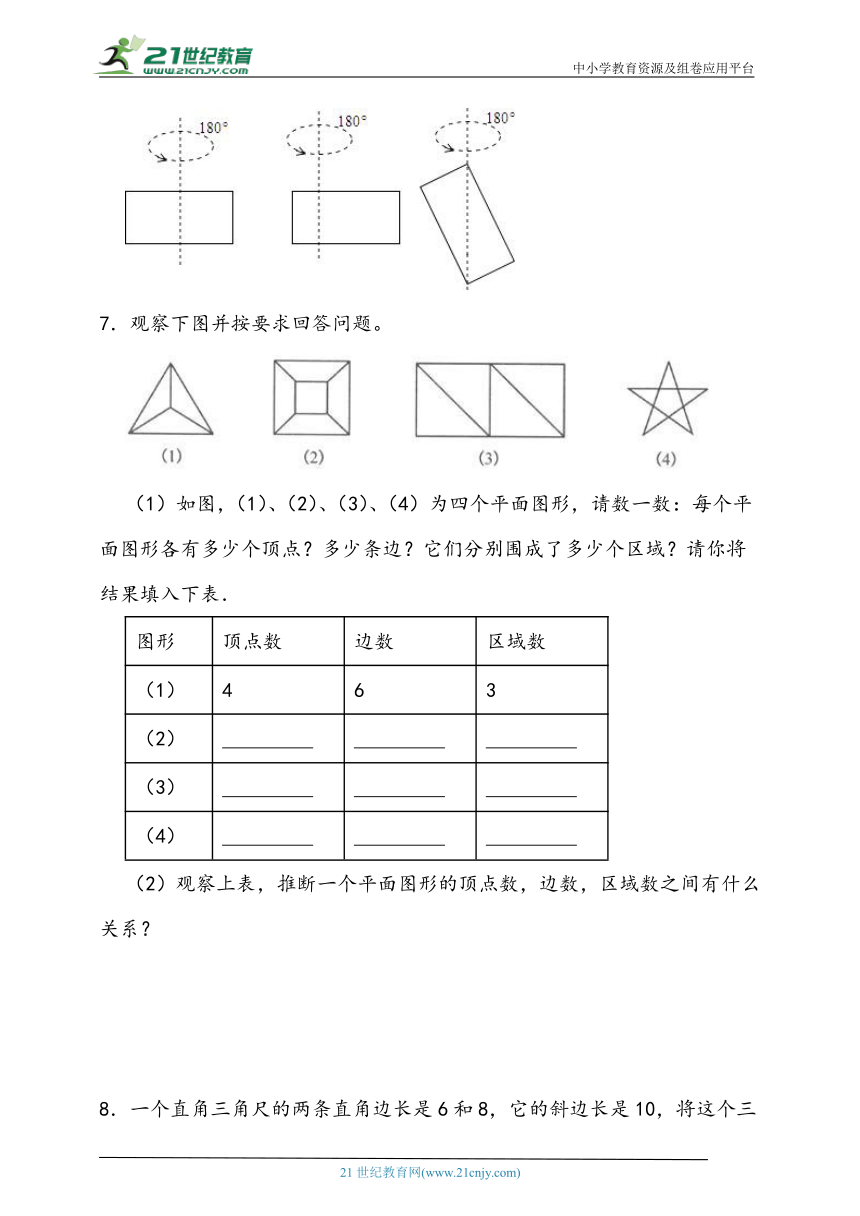
1.当笔尖在纸上移动时,形成 ,这说明: ;表针旋转时,形成了一个 ,这说明: ;长方形纸片绕它的一边旋转,形成的几何图形就是 ,这说明: .
2.如图,下面的几何体是由图 (填写序号)的平面图形绕直线旋转一周得到的.
3.将一个直角三角形ABC绕它的一边旋转,旋转后所得的几何体可能是下面图中的哪个 .
4.长方形的两条边长分别为3cm和4cm,以其中一条边所在的直线为轴旋转一周后得到几何体的底面积是 .
5.已知长方形长为5,宽为2,将其绕它的一条边所在的直线旋转一周,得到一个几何体,该几何体的体积为 .(结果保留 )
6.如图,画出旋转过程中得到的立体图形的示意图.
7.观察下图并按要求回答问题。
(1)如图,(1)、(2)、(3)、(4)为四个平面图形,请数一数:每个平面图形各有多少个顶点?多少条边?它们分别围成了多少个区域?请你将结果填入下表.
图形 顶点数 边数 区域数
(1) 4 6 3
(2)
(3)
(4)
(2)观察上表,推断一个平面图形的顶点数,边数,区域数之间有什么关系?
8.一个直角三角尺的两条直角边长是6和8,它的斜边长是10,将这个三角尺绕着它的一边所在的直线旋转一周.(温馨提示:①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体=πR3,V圆锥=πr2h).
(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是 .
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
几何体的表面积
9.一位画家把7个边长为1m的相同正方体摆成如图的形状,然后把露出的表面(不包括底面)涂上颜色,则涂色面积为 m2.
10.如图,三棱柱的底面边长都为2 cm,侧棱长为5 cm,则这个三棱柱的侧面展开图的面积为 .
11.如图,在棱长分别为 、 、 的长方体中截掉一个棱长为 的正方体,则剩余几何体的表面积为 .
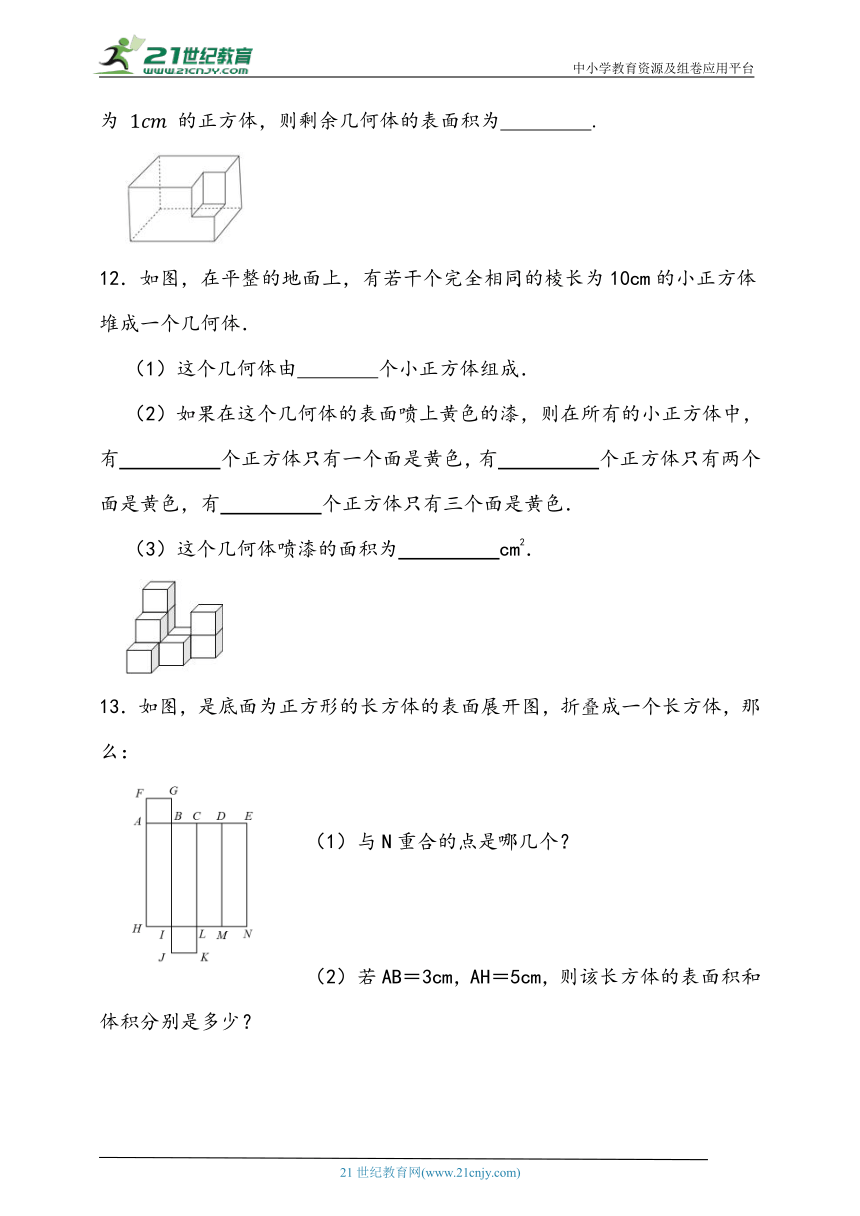
12.如图,在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体.
(1)这个几何体由 个小正方体组成.
(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有 个正方体只有一个面是黄色,有 个正方体只有两个面是黄色,有 个正方体只有三个面是黄色.
(3)这个几何体喷漆的面积为 cm2.
13.如图,是底面为正方形的长方体的表面展开图,折叠成一个长方体,那么:
(1)与N重合的点是哪几个?
若AB=3cm,AH=5cm,则该长方体的表面积和体积分别是多少?
截一个几何体
14.如图,用一个平面去截一个三棱柱,截面的形状可能是 .
①三角形②四边形③五边形④六边形
15.若用平面分别截下列几何体:①三棱柱;②三棱锥;③正方体;④圆锥;⑤球,得到的截面不可能是三角形的是 .(填写正确的几何体前的序号)
16.如图所示,截去正方体一角变成一个新的多面体,这个多面体有 个面;截去的几何体有 个面,图中阴影表示的截面形状是 三角形.
17.分别指出图中几何体的截面形状的标号:
(1)中截面形状的标号: ;
(2)中截面形状的标号: ;
(3)中截面形状的标号: .
18.用一个平面去截一个正方体,可以得到几边形?将得到的图形分别画在下面的备用图中.
19.如图所示.长方形ABCD的周长是32cm,且5AD=3AB,把长方形ABCD绕直线AB旋转一周,然后用平面沿线段AB的方向截所得的几何体,求截面的最大面积.
答案解析部分
1.【答案】一条线;点动成 线;圆面;线动成面;圆柱体;面动成体
2.【答案】②
3.【答案】(2)(3)(4)
4.【答案】9πcm2或16πcm2
5.【答案】 或
6.【答案】解:如图所示:
7.【答案】(1)8;12;5;6;9;4;10;15;6
(2)平面图形的顶点数、区域数、边数的关系是:顶点数+区域数=边数+1
8.【答案】解:(1)两个圆锥形成的几何体,
故答案为:两个圆锥形成的几何体.
(2)V圆锥=πr2h=π×82×6=128π,
(3)①如图=,解得r=,
所以绕着斜边10所在的直线旋转一周形成的几何体的体积为V圆锥=πr2h=π×()2×10=76.8π
②绕着直角边8所在的直线旋转一周形成的几何体的体积为V圆锥=πr2h=π×62×8=96π,
故绕着直角边8所在的直线旋转一周形成的几何体的体积大.
9.【答案】23
10.【答案】30 cm2
11.【答案】
12.【答案】解:(1)这个几何体由 10个小正方体组成.
(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有 1个正方体只有一个面是黄色,有 2个正方体只有两个面是黄色,有 3个正方体只有三个面是黄色.
(3)露出表面的面一共有32个,则这个几何体喷漆的面积为3200cm2,
故答案为:10;1,2,3;3200.
13.【答案】(1)解:与N重合的点有点H和点J.
(2)解:∵长方体的底面为正方形,
由长方体展开图可知:
AB=BC=3cm,而AH=5cm,
∴长方体的长、宽、高分别为:5cm,3cm,3cm,
∴长方体的表面积为: ,
体积为: .
14.【答案】①②③
15.【答案】⑤
16.【答案】7;4;等边
17.【答案】(1)①
(2)③
(3)③
18.【答案】解:如图所示:用一个平面去截正方体,所得截面可能是三角形、四边形(梯形,矩形,正方形)、五边形、六边形.
19.【答案】解:设AD=x,AB=y.
根据题意得:
解得:x=6,y=10.
∴AD=6,AB=10.
∴圆柱体的直径为12,高为10.
∴截面的最大面积=12×10=120cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章 图形的初步认识
点、线、面、体
点、线、面、体及之间的联系
1.当笔尖在纸上移动时,形成 ,这说明: ;表针旋转时,形成了一个 ,这说明: ;长方形纸片绕它的一边旋转,形成的几何图形就是 ,这说明: .
2.如图,下面的几何体是由图 (填写序号)的平面图形绕直线旋转一周得到的.
3.将一个直角三角形ABC绕它的一边旋转,旋转后所得的几何体可能是下面图中的哪个 .
4.长方形的两条边长分别为3cm和4cm,以其中一条边所在的直线为轴旋转一周后得到几何体的底面积是 .
5.已知长方形长为5,宽为2,将其绕它的一条边所在的直线旋转一周,得到一个几何体,该几何体的体积为 .(结果保留 )
6.如图,画出旋转过程中得到的立体图形的示意图.
7.观察下图并按要求回答问题。
(1)如图,(1)、(2)、(3)、(4)为四个平面图形,请数一数:每个平面图形各有多少个顶点?多少条边?它们分别围成了多少个区域?请你将结果填入下表.
图形 顶点数 边数 区域数
(1) 4 6 3
(2)
(3)
(4)
(2)观察上表,推断一个平面图形的顶点数,边数,区域数之间有什么关系?
8.一个直角三角尺的两条直角边长是6和8,它的斜边长是10,将这个三角尺绕着它的一边所在的直线旋转一周.(温馨提示:①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体=πR3,V圆锥=πr2h).
(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是 .
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
几何体的表面积
9.一位画家把7个边长为1m的相同正方体摆成如图的形状,然后把露出的表面(不包括底面)涂上颜色,则涂色面积为 m2.
10.如图,三棱柱的底面边长都为2 cm,侧棱长为5 cm,则这个三棱柱的侧面展开图的面积为 .
11.如图,在棱长分别为 、 、 的长方体中截掉一个棱长为 的正方体,则剩余几何体的表面积为 .
12.如图,在平整的地面上,有若干个完全相同的棱长为10cm的小正方体堆成一个几何体.
(1)这个几何体由 个小正方体组成.
(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有 个正方体只有一个面是黄色,有 个正方体只有两个面是黄色,有 个正方体只有三个面是黄色.
(3)这个几何体喷漆的面积为 cm2.
13.如图,是底面为正方形的长方体的表面展开图,折叠成一个长方体,那么:
(1)与N重合的点是哪几个?
若AB=3cm,AH=5cm,则该长方体的表面积和体积分别是多少?
截一个几何体
14.如图,用一个平面去截一个三棱柱,截面的形状可能是 .
①三角形②四边形③五边形④六边形
15.若用平面分别截下列几何体:①三棱柱;②三棱锥;③正方体;④圆锥;⑤球,得到的截面不可能是三角形的是 .(填写正确的几何体前的序号)
16.如图所示,截去正方体一角变成一个新的多面体,这个多面体有 个面;截去的几何体有 个面,图中阴影表示的截面形状是 三角形.
17.分别指出图中几何体的截面形状的标号:
(1)中截面形状的标号: ;
(2)中截面形状的标号: ;
(3)中截面形状的标号: .
18.用一个平面去截一个正方体,可以得到几边形?将得到的图形分别画在下面的备用图中.
19.如图所示.长方形ABCD的周长是32cm,且5AD=3AB,把长方形ABCD绕直线AB旋转一周,然后用平面沿线段AB的方向截所得的几何体,求截面的最大面积.
答案解析部分
1.【答案】一条线;点动成 线;圆面;线动成面;圆柱体;面动成体
2.【答案】②
3.【答案】(2)(3)(4)
4.【答案】9πcm2或16πcm2
5.【答案】 或
6.【答案】解:如图所示:
7.【答案】(1)8;12;5;6;9;4;10;15;6
(2)平面图形的顶点数、区域数、边数的关系是:顶点数+区域数=边数+1
8.【答案】解:(1)两个圆锥形成的几何体,
故答案为:两个圆锥形成的几何体.
(2)V圆锥=πr2h=π×82×6=128π,
(3)①如图=,解得r=,
所以绕着斜边10所在的直线旋转一周形成的几何体的体积为V圆锥=πr2h=π×()2×10=76.8π
②绕着直角边8所在的直线旋转一周形成的几何体的体积为V圆锥=πr2h=π×62×8=96π,
故绕着直角边8所在的直线旋转一周形成的几何体的体积大.
9.【答案】23
10.【答案】30 cm2
11.【答案】
12.【答案】解:(1)这个几何体由 10个小正方体组成.
(2)如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有 1个正方体只有一个面是黄色,有 2个正方体只有两个面是黄色,有 3个正方体只有三个面是黄色.
(3)露出表面的面一共有32个,则这个几何体喷漆的面积为3200cm2,
故答案为:10;1,2,3;3200.
13.【答案】(1)解:与N重合的点有点H和点J.
(2)解:∵长方体的底面为正方形,
由长方体展开图可知:
AB=BC=3cm,而AH=5cm,
∴长方体的长、宽、高分别为:5cm,3cm,3cm,
∴长方体的表面积为: ,
体积为: .
14.【答案】①②③
15.【答案】⑤
16.【答案】7;4;等边
17.【答案】(1)①
(2)③
(3)③
18.【答案】解:如图所示:用一个平面去截正方体,所得截面可能是三角形、四边形(梯形,矩形,正方形)、五边形、六边形.
19.【答案】解:设AD=x,AB=y.
根据题意得:
解得:x=6,y=10.
∴AD=6,AB=10.
∴圆柱体的直径为12,高为10.
∴截面的最大面积=12×10=120cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
