2022-2023学年河北省石家庄市赵县七年级(下)期末数学试卷(含解析)
文档属性
| 名称 | 2022-2023学年河北省石家庄市赵县七年级(下)期末数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 436.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 19:02:25 | ||
图片预览




文档简介
2022-2023学年河北省石家庄市赵县七年级(下)期末数学试卷
一、选择题(本大题共16小题,共48.0分。在每小题列出的选项中,选出符合题目的一项)
1. 如图,直线,相交于点,,垂足为若,则的度数为( )
A. B. C. D.
2. 一个容量为的样本最大值为,最小值为,取组距为,则可以分成( )
A. 组 B. 组 C. 组 D. 组
3. 下列各组数中,互为相反数的是( )
A. 与 B. 与 C. 与 D. 与
4. 某班共有名学生,在一次体育抽测中有人不合格,则不合格学生的频率为( )
A. B. C. D.
5. 下列各数中,与的和为有理数的是( )
A. B. C. D.
6. 二元一次方程的一个解是( )
A. B. C. D.
7. 如图,三角形沿方向平移到三角形的位置,若,,则平移的距离为.( )
A. B. C. D.
8. 如图,已知,为保证两条铁轨平行,添加的下列条件中,正确的是
A. B. C. D.
9. 下列命题:
经过直线外一点,有且只有一条直线与这条直线平行;
在同一平面内,过一点有且只有一条直线与已知直线垂直;
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;
如果直线,,那么.
其中是真命题的有个( )
A. 个 B. 个 C. 个 D. 个
10. 如图,是一块直角三角板,其中,直尺的一边经过顶点,若,则的度数为( )
A. B. C. D.
11. 在平面直角坐标系中,线段轴,则( )
A. 点与的横坐标相等 B. 点与的纵坐标相等
C. 点与的横坐标与纵坐标分别相等 D. 点与的横坐标、纵坐标都不相等
12. 为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神,湘潭市举办了第届青少年机器人竞赛.组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共个,若桌子腿数与凳子腿数的和为条,则每个比赛场地有几张桌子和几条凳子?设有张桌子,有条凳子,根据题意所列方程组正确的是( )
A. B. C. D.
13. 如果不等式的解集为,那么的取值范围是( )
A. B. C. D.
14. 如图,光在不同介质中的传播速度是不同的,因此当光线从水中射向空气时;要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,,,则的度数为
A. B. C. D.
15. 某品牌护眼灯的进价为元,商店以元的价格出售,“五一节”期间,商店为让利于顾客,计划以利润率不低于的价格降价出售,则该护眼灯最多可降价元( )
A.
B.
C.
D.
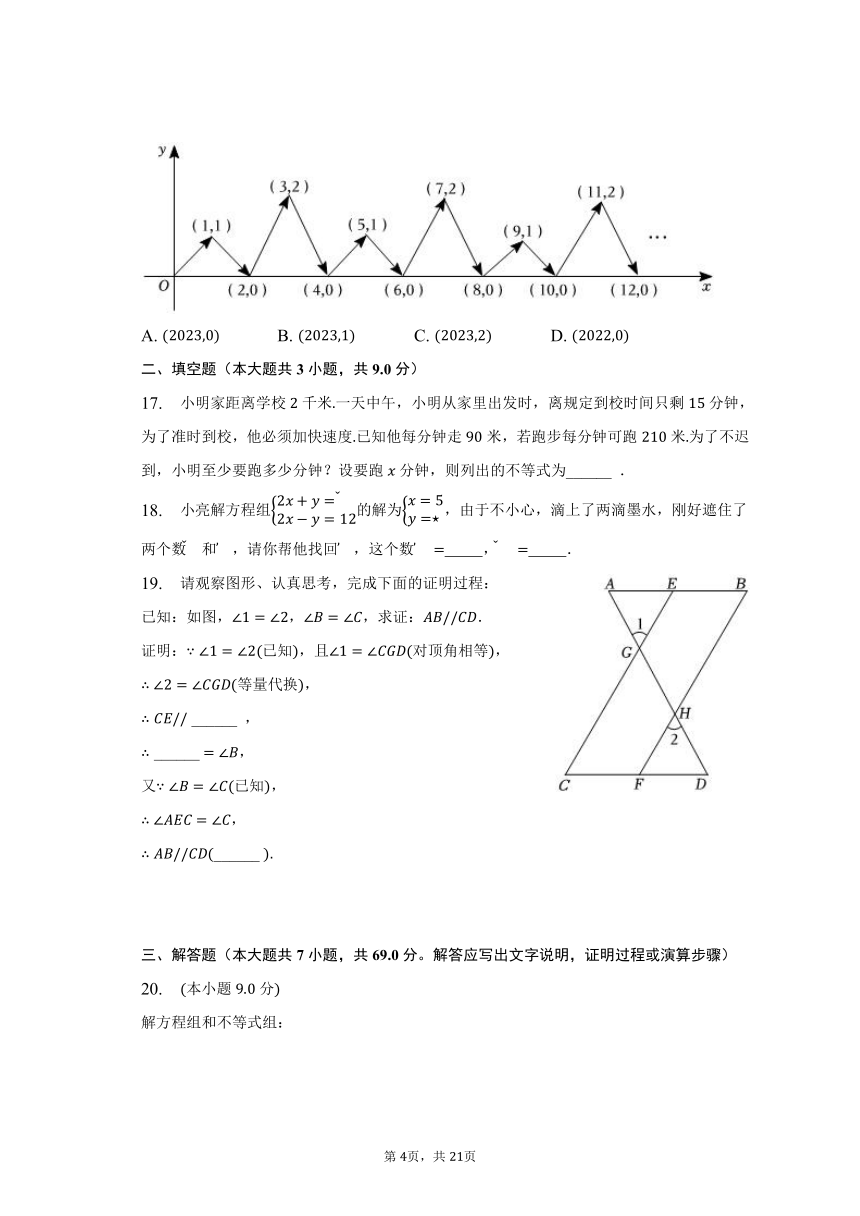
16. 如图,动点按图中箭头所示方向运动,第次从原点运动到点,第次运动到点,第次运动到点,,按这样的运动规律,则第次运动到点( )
A. B. C. D.
二、填空题(本大题共3小题,共9.0分)
17. 小明家距离学校千米一天中午,小明从家里出发时,离规定到校时间只剩分钟,为了准时到校,他必须加快速度已知他每分钟走米,若跑步每分钟可跑米为了不迟到,小明至少要跑多少分钟?设要跑分钟,则列出的不等式为______ .
18. 小亮解方程组的解为,由于不小心,滴上了两滴墨水,刚好遮住了两个数和,请你帮他找回,这个数 , .
19. 请观察图形、认真思考,完成下面的证明过程:
已知:如图,,,求证:.
证明:已知,且对顶角相等,
等量代换,
______ ,
______ ,
又已知,
,
______
三、解答题(本大题共7小题,共69.0分。解答应写出文字说明,证明过程或演算步骤)
20. 本小题分
解方程组和不等式组:
解方程组:;
解不等式组:.
21. 本小题分
问题:在一块面积为的正方形纸片上,沿着边的方向裁出一块面积为,且长宽之比为:的长方形纸片不拼接,能裁出吗?请说出理由.
22. 本小题分
我国古代数学名著九章算术中有这样一个问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”其大意是:今有几个人共同出钱购买一件物品.每人出钱,剩余钱;每人出钱,还缺钱.问人数、物品价格各是多少?请你求出以上问题中的人数和物品价格.
23. 本小题分
已知当、都是实数,且满足,则称点为“智慧点”.
判断点是否为“智慧点”,并说明理由.
若点是“智慧点”请判断点在第几象限?并说明理由.
24. 本小题分
在很多情况下,一个命题的正确性需要经过推理才能做出判断,这个推理过程叫做证明求证:两条直线平行,一组内错角的平分线互相平行.
25. 本小题分
首届全民阅读大会于年月日在北京开幕,大会主题是“阅读新时代奋进新征程”某校“综合与实践”小组为了解全校名学生的读书情况,随机抽取部分学生进行问卷调查,形成了如下调查报告不完整:
中学学生读书情况调查报告
调查主题 中学学生读书情况
调查方式 抽样调查 调查对象 中学学生
数据的收集、整理与描述 第一项 您平均每周阅读课外书的时间大约是只能单选,每项含最小值,不含最大值
A.小时及以上;
B.小时;
C.小时;
D.小时.
第二项 您阅读的课外书的主要来源是可多选
E.自行购买;
F.从图书馆借阅;
G.免费数字阅读;
H.向他人借阅.
调查结论
请根据以上调查报告,解答下列问题:
求参与本次抽样调查的学生人数及这些学生中选择“从图书馆借阅”的人数;
估计该校名学生中,平均每周阅读课外书时间在“小时及以上”的人数;
该小组要根据以上调查报告在全班进行交流,假如你是小组成员,请结合以上两项调查数据分别写出一条你获取的信息.
26. 本小题分
我市某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下型与型两种板材.如图甲,单位:
列出方程组,求出图甲中与的值;
在试生产阶段,若将张标准板材用裁法一裁剪,张标准板材用裁法二裁剪,再将得到的型与型板材做侧面和底面,做成图乙的竖式与横式两种礼品盒.
两种裁法共产生型板材______ 张,型板材______ 张;
已知中的型板材和型板材恰好做成竖式有盖礼品盒个,横式无盖礼品盒的个,求、的值.
答案和解析
1.【答案】
【解析】解:,
,
,
.
故选:.
首先利用垂直的定义得到,然后利用平角的定义即可求解.
本题主要考查了垂直的定义和平角的定义,要注意领会由垂直得直角这一要点.
2.【答案】
【解析】解:在样本数据中最大值为,最小值为,它们的差是,已知组距为,那么由于,故可以分成组.
故选:.
根据组数最大值最小值组距计算,注意小数部分要进位.
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
3.【答案】
【解析】解:和,两数是互为相反数,故此选项符合题意;
B.与,两数不是互为相反数,故此选项不合题意;
C.与,两数不是互为相反数,故此选项不合题意;
D.与,两数不是互为相反数,故此选项不合题意.
故选:.
直接利用立方根的性质以及绝对值的性质、二次根式的性质分别化简,进而判断即可.
此题主要考查了实数的性质,正确化简各数是解题关键.
4.【答案】
【解析】解:由题意得:,
不合格学生的频率为,
故选:.
根据频率频数总次数,进行计算即可解答.
本题考查了频数与频率,熟练掌握频率频数总次数是解题的关键.
5.【答案】
【解析】解:、,和为无理数,故此选项不符合题意;
B、,和为无理数,故此选项不符合题意;
C、,和为无理数,故此选项不符合题意;
D、,和为有理数,故此选项符合题意;
故选:.
根据二次根式的加法法则分别计算,再根据有理数的定义判断即可.
本题考查了二次根式的加减法以及无理数、有理数的定义,熟练掌握二次根式的加减法法则是解题的关键.
6.【答案】
【解析】解:、,能使方程成立,故该选项正确,符合题意;
B、,不能使方程成立,故该选项不正确,不符合题意;
C、,不能使方程成立,故该选项不正确,不符合题意;
D、,不能使方程成立,故该选项不正确,不符合题意.
故选:.
分别将选项中的解代入方程,使等式成立的即是它的解.
此题主要考查二元一次方程的解,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
7.【答案】
【解析】解:三角形沿着的方向平移得到三角形,
,平移的距离为的长,
,,
,
三角形移动的距离是.
故选:.
根据平移的性质得到,平移的距离为的长,然后利用求出即可.
本题考查平移的性质:平移不改变图形的形状和大小;经过平移,对应点所连的线段平行或共线且相等,对应线段平行且相等,对应角相等.
8.【答案】
【解析】解:由不能判定两条铁轨平行,故该选项不符合题意;
B.由,可判定两枕木平行,故该选项不符合题意;
C.,,
,
两条铁轨平行,故该选项符合题意;
D.由不能判定两条铁轨平行,故该选项不符合题意;
故选:.
根据平行线的判定逐项分析即可得到结论.
本题主要考查了平行线的判定,熟练掌握平行线的判定方法是解决问题的关键.
9.【答案】
【解析】解:经过直线外一点,有且只有一条直线与这条直线平行,正确,是真命题,符合题意;
在同一平面内,过一点有且只有一条直线与已知直线垂直,正确,是真命题,符合题意;
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,正确,是真命题,符合题意;
如果直线,,那么,故原命题错误,是假命题,不符合题意.
真命题有个,
故选:.
利用平行线的判定、垂直的性质、点到直线的距离的定义等知识分别判断后即可确定正确的选项.
本题考查了命题与定理的知识,解题的关键是了解有关定义及定理,难度不大.
10.【答案】
【解析】解:,,
,
,
,
故答案为:.
先根据平行线的性质求得的度数,再根据角的和差关系求得结果.
本题主要考查了平行线的性质以及三角形角和差计算,关键是利用平行线的性质求得.
11.【答案】
【解析】解:根据线段轴,则点与的纵坐标相等.
故选:.
平行于轴的直线上所有点的纵坐标相等,平行于轴的直线上所有点的横坐标相等.
此题考查了平行于轴的直线和平行于轴的直线上点的坐标特征.
12.【答案】
【解析】
【分析】
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
根据“组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共个,且桌子腿数与凳子腿数的和为条”,即可得出关于,的二元一次方程组,此题得解.
【解答】
解:组委会为每个比赛场地准备了桌子和凳子共个,
;
又桌子腿数与凳子腿数的和为条,且每张桌子有条腿,每条凳子有条腿,
.
列出的方程组为.
故选:.
13.【答案】
【解析】解:的解集为,
,
解得:.
故选:.
利用不等式的基本性质确定出的范围即可.
此题考查了解一元一次不等式,熟练掌握不等式的解法是解本题的关键.
14.【答案】
【解析】解:如图所示:
,,
,
,
,
,
.
,
.
故选:.
先根据得出的度数,再由得出的度数,根据即可得出结论.
本题考查的是平行线的性质,关键是熟练掌握两直线平行,内错角相等;两直线平行,同位角相等;两直线平行,同旁内角互补.
15.【答案】
【解析】解:设该护眼灯可降价元,
根据题意得:,
解得:,
的最大值为,
即该护眼灯最多可降价元.
故选:.
设该护眼灯可降价元,利用利润售价进价,结合利润率不低于,可列出关于的一元一次不等式,解之可得出的取值范围,再取其中的最大值,即可得出结论.
本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
16.【答案】
【解析】解:由题意可知,第次从原点运动到点,
第次接着运动到点,
第次接着运动到点,
第次从原点运动到点,
第次接着运动到点,
第次接着运动到点,
第次接着运动到点,
第次接着运动到点,
第次从原点运动到点,
第次接着运动到点,
,
第次接着运动到点,
故选:.
根据前几次运动的规律可知第次接着运动到点,第次接着运动到点,第次从原点运动到点,第次接着运动到点,根据规律求解即可.
本题考查了点的坐标规律型问题,解题的关键是根据点的坐标的变化得到规律,利用得到的规律解题.
17.【答案】
【解析】解:由题意得:.
故答案为:.
设要跑分钟,则走分钟,根据题意列出不等式解答即可.
此题考查由实际问题抽象出一元一次不等式,关键是根据题意找出不等关系列出不等式.
18.【答案】
【解析】
【分析】
把代入方程组的第二个方程求出的值,将与的值代入第一个方程左边即可得到结果.
此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.
【解答】
解:把代入中,得:,
当,时,,
故答案为:;.
19.【答案】 内错角相等,两直线平行
【解析】解:已知,且对顶角相等,
等量代换,
,
,
又已知,
,
内错角相等,两直线平行,
故答案为:;;内错角相等,两直线平行.
先根据对顶角相等可得,从而可得,然后利用同位角相等,两直线平行可得,从而可得,进而可得,最后根据内错角相等,两直线平行可得,即可解答.
本题考查了平行线的判定与性质,根据题目的已知条件并结合图形进行分析是解题的关键.
20.【答案】解:;
得:,
解得:,
把代入中得:,
解得:.
原方程组的解为:;
,
解不等式得:;
解不等式得:;
原不等式组的解集为:.
【解析】利用加减消元法进行计算,即可解答;
按照解一元一次不等式组的步骤,进行计算即可解答.
本题考查了解二元一次方程组,解一元一次不等式组,准确熟练地进行计算是解题的关键.
21.【答案】解:不能裁出,
理由如下:设长方形的长是,则宽是,由题意可得:
,
,
,
或舍去,
长是 ,宽是 ,
正方形纸片的面积为,则边长为 ,即边长为,
,,
,
裁不出.
【解析】由题意求出要裁出的长方形纸片的长与宽,比较长方形的长与正方形的边长的大小,即可得到答案.
本题考查算术平方根,关键是列出方程由算术平方根的定义求出长方形的长与宽.
22.【答案】解:设有个人,物品的价格为钱,
由题意得:,解得:,
答:有个人,物品的价格为钱.
【解析】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
设有个人,物品的价格为钱,由题意:每人出钱,剩余钱;每人出钱,还缺钱.列出二元一次方程组,解方程组即可.
23.【答案】解:点不是“智慧点”,
由题意得:,
,,
,
,
,
点不是“智慧点”;
点在第四象限,
理由:点是“智慧点”,
,
,,
,
,
解得,
点,
点在第四象限.
【解析】根据点坐标,代入中,求出和的值,然后代入,检验等号是否成立即可;
直接利用“智慧点”的定义得出的值进而得出答案.
本题考查了点的坐标,掌握“智慧点”的定义是关键.
24.【答案】已知:如图,直线,被直线所截,交点分别为、,且,平分,平分,
求证:,
证明:,
,
平分,平分,
,,
,
.
【解析】先根据命题的条件和结论画出图形,并写出已知和求证,然后根据平行线的性质可得,再根据角平分线的定义可得,,从而利用等量代换可得,最后根据内错角相等,两直线平行可得,即可解答.
本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解题的关键.
25.【答案】解:平均每周阅读课外书的时间大约是小时的人数为人,占抽样学生人数的,
参与本次抽样调查的学生人数为:人,
从图书馆借阅的人数占总数人的,
选择“从图书馆借阅”的人数为:人,
答:参与本次抽样调查的学生人数为人,选择“从图书馆借阅”的人数为人;
平均每周阅读课外书时间在“小时及以上”的人数占比为,
人,
答:该校名学生中,平均每周阅读课外书时间在“小时及以上”的人数为人;
答案不唯一,如:
由第一项可知:
阅读时间为“小时”的人数最多,“小时”的人数最少,
由第二项可知:
阅读的课外书的主要来源中“从图书馆借阅”的人数最多,“向他人借阅”的人数最少.
【解析】由条形统计图和扇形统计图可得平均每周阅读课外书的时间大约是小时的人数为人,占抽样学生人数的,即可求解,由条形统计图可知从图书馆借阅的人数占总数人的,即可求解;
由扇形统计图可知平均每周阅读课外书时间在“小时及以上”的人数占比为,即可求解;
由第一项可知阅读时间为“小时”的人数最多,“小时”的人数最少,由第二项可知阅读的课外书的主要来源中“从图书馆借阅”的人数最多,“向他人借阅”的人数最少等等.
本题考查条形统计图,扇形统计图,用样本估计总体等知识点,解题的关键是掌握利用统计图提取所需信息.
26.【答案】由题意得:,
解得:,
答:图甲中与的值分别为:、
;;
根据题意竖式有盖礼品盒的个,横式无盖礼品盒的个,则型板材需要个,型板材需要个,
所以,
解得,
所以恰好做成竖式有盖礼品盒个,横式无盖礼品盒的个.
【解析】解:由题意得:,
解得:,
答:图甲中与的值分别为:、;
由图示裁法一产生型板材为:,裁法二产生型板材为:,
所以两种裁法共产生型板材为张,
由图示裁法一产生型板材为:,裁法二产生型板材为,,
所以两种裁法共产生型板材为张,
故答案为:,;
根据题意竖式有盖礼品盒的个,横式无盖礼品盒的个,
则型板材需要个,型板材需要个,
所以,
解得.
由图示利用板材的长列出关于、的二元一次方程组求解;
根据已知和图示计算出两种裁法共产生型板材和型板材的张数;
根据竖式与横式礼品盒所需要的、两种型号板材的张数列出关于、的二元一次方程组,然后求解即可.
本题考查的知识点是二元一次方程组的应用,关键是根据已知先列出二元一次方程组求出、的值,根据图示列出算式以及关于、的二元一次方程组.
第1页,共1页
一、选择题(本大题共16小题,共48.0分。在每小题列出的选项中,选出符合题目的一项)
1. 如图,直线,相交于点,,垂足为若,则的度数为( )
A. B. C. D.
2. 一个容量为的样本最大值为,最小值为,取组距为,则可以分成( )
A. 组 B. 组 C. 组 D. 组
3. 下列各组数中,互为相反数的是( )
A. 与 B. 与 C. 与 D. 与
4. 某班共有名学生,在一次体育抽测中有人不合格,则不合格学生的频率为( )
A. B. C. D.
5. 下列各数中,与的和为有理数的是( )
A. B. C. D.
6. 二元一次方程的一个解是( )
A. B. C. D.
7. 如图,三角形沿方向平移到三角形的位置,若,,则平移的距离为.( )
A. B. C. D.
8. 如图,已知,为保证两条铁轨平行,添加的下列条件中,正确的是
A. B. C. D.
9. 下列命题:
经过直线外一点,有且只有一条直线与这条直线平行;
在同一平面内,过一点有且只有一条直线与已知直线垂直;
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;
如果直线,,那么.
其中是真命题的有个( )
A. 个 B. 个 C. 个 D. 个
10. 如图,是一块直角三角板,其中,直尺的一边经过顶点,若,则的度数为( )
A. B. C. D.
11. 在平面直角坐标系中,线段轴,则( )
A. 点与的横坐标相等 B. 点与的纵坐标相等
C. 点与的横坐标与纵坐标分别相等 D. 点与的横坐标、纵坐标都不相等
12. 为培养青少年的创新意识、动手实践能力、现场应变能力和团队精神,湘潭市举办了第届青少年机器人竞赛.组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共个,若桌子腿数与凳子腿数的和为条,则每个比赛场地有几张桌子和几条凳子?设有张桌子,有条凳子,根据题意所列方程组正确的是( )
A. B. C. D.
13. 如果不等式的解集为,那么的取值范围是( )
A. B. C. D.
14. 如图,光在不同介质中的传播速度是不同的,因此当光线从水中射向空气时;要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,,,则的度数为
A. B. C. D.
15. 某品牌护眼灯的进价为元,商店以元的价格出售,“五一节”期间,商店为让利于顾客,计划以利润率不低于的价格降价出售,则该护眼灯最多可降价元( )
A.
B.
C.
D.
16. 如图,动点按图中箭头所示方向运动,第次从原点运动到点,第次运动到点,第次运动到点,,按这样的运动规律,则第次运动到点( )
A. B. C. D.
二、填空题(本大题共3小题,共9.0分)
17. 小明家距离学校千米一天中午,小明从家里出发时,离规定到校时间只剩分钟,为了准时到校,他必须加快速度已知他每分钟走米,若跑步每分钟可跑米为了不迟到,小明至少要跑多少分钟?设要跑分钟,则列出的不等式为______ .
18. 小亮解方程组的解为,由于不小心,滴上了两滴墨水,刚好遮住了两个数和,请你帮他找回,这个数 , .
19. 请观察图形、认真思考,完成下面的证明过程:
已知:如图,,,求证:.
证明:已知,且对顶角相等,
等量代换,
______ ,
______ ,
又已知,
,
______
三、解答题(本大题共7小题,共69.0分。解答应写出文字说明,证明过程或演算步骤)
20. 本小题分
解方程组和不等式组:
解方程组:;
解不等式组:.
21. 本小题分
问题:在一块面积为的正方形纸片上,沿着边的方向裁出一块面积为,且长宽之比为:的长方形纸片不拼接,能裁出吗?请说出理由.
22. 本小题分
我国古代数学名著九章算术中有这样一个问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”其大意是:今有几个人共同出钱购买一件物品.每人出钱,剩余钱;每人出钱,还缺钱.问人数、物品价格各是多少?请你求出以上问题中的人数和物品价格.
23. 本小题分
已知当、都是实数,且满足,则称点为“智慧点”.
判断点是否为“智慧点”,并说明理由.
若点是“智慧点”请判断点在第几象限?并说明理由.
24. 本小题分
在很多情况下,一个命题的正确性需要经过推理才能做出判断,这个推理过程叫做证明求证:两条直线平行,一组内错角的平分线互相平行.
25. 本小题分
首届全民阅读大会于年月日在北京开幕,大会主题是“阅读新时代奋进新征程”某校“综合与实践”小组为了解全校名学生的读书情况,随机抽取部分学生进行问卷调查,形成了如下调查报告不完整:
中学学生读书情况调查报告
调查主题 中学学生读书情况
调查方式 抽样调查 调查对象 中学学生
数据的收集、整理与描述 第一项 您平均每周阅读课外书的时间大约是只能单选,每项含最小值,不含最大值
A.小时及以上;
B.小时;
C.小时;
D.小时.
第二项 您阅读的课外书的主要来源是可多选
E.自行购买;
F.从图书馆借阅;
G.免费数字阅读;
H.向他人借阅.
调查结论
请根据以上调查报告,解答下列问题:
求参与本次抽样调查的学生人数及这些学生中选择“从图书馆借阅”的人数;
估计该校名学生中,平均每周阅读课外书时间在“小时及以上”的人数;
该小组要根据以上调查报告在全班进行交流,假如你是小组成员,请结合以上两项调查数据分别写出一条你获取的信息.
26. 本小题分
我市某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下型与型两种板材.如图甲,单位:
列出方程组,求出图甲中与的值;
在试生产阶段,若将张标准板材用裁法一裁剪,张标准板材用裁法二裁剪,再将得到的型与型板材做侧面和底面,做成图乙的竖式与横式两种礼品盒.
两种裁法共产生型板材______ 张,型板材______ 张;
已知中的型板材和型板材恰好做成竖式有盖礼品盒个,横式无盖礼品盒的个,求、的值.
答案和解析
1.【答案】
【解析】解:,
,
,
.
故选:.
首先利用垂直的定义得到,然后利用平角的定义即可求解.
本题主要考查了垂直的定义和平角的定义,要注意领会由垂直得直角这一要点.
2.【答案】
【解析】解:在样本数据中最大值为,最小值为,它们的差是,已知组距为,那么由于,故可以分成组.
故选:.
根据组数最大值最小值组距计算,注意小数部分要进位.
本题考查的是组数的计算,属于基础题,只要根据组数的定义“数据分成的组的个数称为组数”来解即可.
3.【答案】
【解析】解:和,两数是互为相反数,故此选项符合题意;
B.与,两数不是互为相反数,故此选项不合题意;
C.与,两数不是互为相反数,故此选项不合题意;
D.与,两数不是互为相反数,故此选项不合题意.
故选:.
直接利用立方根的性质以及绝对值的性质、二次根式的性质分别化简,进而判断即可.
此题主要考查了实数的性质,正确化简各数是解题关键.
4.【答案】
【解析】解:由题意得:,
不合格学生的频率为,
故选:.
根据频率频数总次数,进行计算即可解答.
本题考查了频数与频率,熟练掌握频率频数总次数是解题的关键.
5.【答案】
【解析】解:、,和为无理数,故此选项不符合题意;
B、,和为无理数,故此选项不符合题意;
C、,和为无理数,故此选项不符合题意;
D、,和为有理数,故此选项符合题意;
故选:.
根据二次根式的加法法则分别计算,再根据有理数的定义判断即可.
本题考查了二次根式的加减法以及无理数、有理数的定义,熟练掌握二次根式的加减法法则是解题的关键.
6.【答案】
【解析】解:、,能使方程成立,故该选项正确,符合题意;
B、,不能使方程成立,故该选项不正确,不符合题意;
C、,不能使方程成立,故该选项不正确,不符合题意;
D、,不能使方程成立,故该选项不正确,不符合题意.
故选:.
分别将选项中的解代入方程,使等式成立的即是它的解.
此题主要考查二元一次方程的解,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
7.【答案】
【解析】解:三角形沿着的方向平移得到三角形,
,平移的距离为的长,
,,
,
三角形移动的距离是.
故选:.
根据平移的性质得到,平移的距离为的长,然后利用求出即可.
本题考查平移的性质:平移不改变图形的形状和大小;经过平移,对应点所连的线段平行或共线且相等,对应线段平行且相等,对应角相等.
8.【答案】
【解析】解:由不能判定两条铁轨平行,故该选项不符合题意;
B.由,可判定两枕木平行,故该选项不符合题意;
C.,,
,
两条铁轨平行,故该选项符合题意;
D.由不能判定两条铁轨平行,故该选项不符合题意;
故选:.
根据平行线的判定逐项分析即可得到结论.
本题主要考查了平行线的判定,熟练掌握平行线的判定方法是解决问题的关键.
9.【答案】
【解析】解:经过直线外一点,有且只有一条直线与这条直线平行,正确,是真命题,符合题意;
在同一平面内,过一点有且只有一条直线与已知直线垂直,正确,是真命题,符合题意;
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,正确,是真命题,符合题意;
如果直线,,那么,故原命题错误,是假命题,不符合题意.
真命题有个,
故选:.
利用平行线的判定、垂直的性质、点到直线的距离的定义等知识分别判断后即可确定正确的选项.
本题考查了命题与定理的知识,解题的关键是了解有关定义及定理,难度不大.
10.【答案】
【解析】解:,,
,
,
,
故答案为:.
先根据平行线的性质求得的度数,再根据角的和差关系求得结果.
本题主要考查了平行线的性质以及三角形角和差计算,关键是利用平行线的性质求得.
11.【答案】
【解析】解:根据线段轴,则点与的纵坐标相等.
故选:.
平行于轴的直线上所有点的纵坐标相等,平行于轴的直线上所有点的横坐标相等.
此题考查了平行于轴的直线和平行于轴的直线上点的坐标特征.
12.【答案】
【解析】
【分析】
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
根据“组委会为每个比赛场地准备了四条腿的桌子和三条腿的凳子共个,且桌子腿数与凳子腿数的和为条”,即可得出关于,的二元一次方程组,此题得解.
【解答】
解:组委会为每个比赛场地准备了桌子和凳子共个,
;
又桌子腿数与凳子腿数的和为条,且每张桌子有条腿,每条凳子有条腿,
.
列出的方程组为.
故选:.
13.【答案】
【解析】解:的解集为,
,
解得:.
故选:.
利用不等式的基本性质确定出的范围即可.
此题考查了解一元一次不等式,熟练掌握不等式的解法是解本题的关键.
14.【答案】
【解析】解:如图所示:
,,
,
,
,
,
.
,
.
故选:.
先根据得出的度数,再由得出的度数,根据即可得出结论.
本题考查的是平行线的性质,关键是熟练掌握两直线平行,内错角相等;两直线平行,同位角相等;两直线平行,同旁内角互补.
15.【答案】
【解析】解:设该护眼灯可降价元,
根据题意得:,
解得:,
的最大值为,
即该护眼灯最多可降价元.
故选:.
设该护眼灯可降价元,利用利润售价进价,结合利润率不低于,可列出关于的一元一次不等式,解之可得出的取值范围,再取其中的最大值,即可得出结论.
本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
16.【答案】
【解析】解:由题意可知,第次从原点运动到点,
第次接着运动到点,
第次接着运动到点,
第次从原点运动到点,
第次接着运动到点,
第次接着运动到点,
第次接着运动到点,
第次接着运动到点,
第次从原点运动到点,
第次接着运动到点,
,
第次接着运动到点,
故选:.
根据前几次运动的规律可知第次接着运动到点,第次接着运动到点,第次从原点运动到点,第次接着运动到点,根据规律求解即可.
本题考查了点的坐标规律型问题,解题的关键是根据点的坐标的变化得到规律,利用得到的规律解题.
17.【答案】
【解析】解:由题意得:.
故答案为:.
设要跑分钟,则走分钟,根据题意列出不等式解答即可.
此题考查由实际问题抽象出一元一次不等式,关键是根据题意找出不等关系列出不等式.
18.【答案】
【解析】
【分析】
把代入方程组的第二个方程求出的值,将与的值代入第一个方程左边即可得到结果.
此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.
【解答】
解:把代入中,得:,
当,时,,
故答案为:;.
19.【答案】 内错角相等,两直线平行
【解析】解:已知,且对顶角相等,
等量代换,
,
,
又已知,
,
内错角相等,两直线平行,
故答案为:;;内错角相等,两直线平行.
先根据对顶角相等可得,从而可得,然后利用同位角相等,两直线平行可得,从而可得,进而可得,最后根据内错角相等,两直线平行可得,即可解答.
本题考查了平行线的判定与性质,根据题目的已知条件并结合图形进行分析是解题的关键.
20.【答案】解:;
得:,
解得:,
把代入中得:,
解得:.
原方程组的解为:;
,
解不等式得:;
解不等式得:;
原不等式组的解集为:.
【解析】利用加减消元法进行计算,即可解答;
按照解一元一次不等式组的步骤,进行计算即可解答.
本题考查了解二元一次方程组,解一元一次不等式组,准确熟练地进行计算是解题的关键.
21.【答案】解:不能裁出,
理由如下:设长方形的长是,则宽是,由题意可得:
,
,
,
或舍去,
长是 ,宽是 ,
正方形纸片的面积为,则边长为 ,即边长为,
,,
,
裁不出.
【解析】由题意求出要裁出的长方形纸片的长与宽,比较长方形的长与正方形的边长的大小,即可得到答案.
本题考查算术平方根,关键是列出方程由算术平方根的定义求出长方形的长与宽.
22.【答案】解:设有个人,物品的价格为钱,
由题意得:,解得:,
答:有个人,物品的价格为钱.
【解析】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.
设有个人,物品的价格为钱,由题意:每人出钱,剩余钱;每人出钱,还缺钱.列出二元一次方程组,解方程组即可.
23.【答案】解:点不是“智慧点”,
由题意得:,
,,
,
,
,
点不是“智慧点”;
点在第四象限,
理由:点是“智慧点”,
,
,,
,
,
解得,
点,
点在第四象限.
【解析】根据点坐标,代入中,求出和的值,然后代入,检验等号是否成立即可;
直接利用“智慧点”的定义得出的值进而得出答案.
本题考查了点的坐标,掌握“智慧点”的定义是关键.
24.【答案】已知:如图,直线,被直线所截,交点分别为、,且,平分,平分,
求证:,
证明:,
,
平分,平分,
,,
,
.
【解析】先根据命题的条件和结论画出图形,并写出已知和求证,然后根据平行线的性质可得,再根据角平分线的定义可得,,从而利用等量代换可得,最后根据内错角相等,两直线平行可得,即可解答.
本题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解题的关键.
25.【答案】解:平均每周阅读课外书的时间大约是小时的人数为人,占抽样学生人数的,
参与本次抽样调查的学生人数为:人,
从图书馆借阅的人数占总数人的,
选择“从图书馆借阅”的人数为:人,
答:参与本次抽样调查的学生人数为人,选择“从图书馆借阅”的人数为人;
平均每周阅读课外书时间在“小时及以上”的人数占比为,
人,
答:该校名学生中,平均每周阅读课外书时间在“小时及以上”的人数为人;
答案不唯一,如:
由第一项可知:
阅读时间为“小时”的人数最多,“小时”的人数最少,
由第二项可知:
阅读的课外书的主要来源中“从图书馆借阅”的人数最多,“向他人借阅”的人数最少.
【解析】由条形统计图和扇形统计图可得平均每周阅读课外书的时间大约是小时的人数为人,占抽样学生人数的,即可求解,由条形统计图可知从图书馆借阅的人数占总数人的,即可求解;
由扇形统计图可知平均每周阅读课外书时间在“小时及以上”的人数占比为,即可求解;
由第一项可知阅读时间为“小时”的人数最多,“小时”的人数最少,由第二项可知阅读的课外书的主要来源中“从图书馆借阅”的人数最多,“向他人借阅”的人数最少等等.
本题考查条形统计图,扇形统计图,用样本估计总体等知识点,解题的关键是掌握利用统计图提取所需信息.
26.【答案】由题意得:,
解得:,
答:图甲中与的值分别为:、
;;
根据题意竖式有盖礼品盒的个,横式无盖礼品盒的个,则型板材需要个,型板材需要个,
所以,
解得,
所以恰好做成竖式有盖礼品盒个,横式无盖礼品盒的个.
【解析】解:由题意得:,
解得:,
答:图甲中与的值分别为:、;
由图示裁法一产生型板材为:,裁法二产生型板材为:,
所以两种裁法共产生型板材为张,
由图示裁法一产生型板材为:,裁法二产生型板材为,,
所以两种裁法共产生型板材为张,
故答案为:,;
根据题意竖式有盖礼品盒的个,横式无盖礼品盒的个,
则型板材需要个,型板材需要个,
所以,
解得.
由图示利用板材的长列出关于、的二元一次方程组求解;
根据已知和图示计算出两种裁法共产生型板材和型板材的张数;
根据竖式与横式礼品盒所需要的、两种型号板材的张数列出关于、的二元一次方程组,然后求解即可.
本题考查的知识点是二元一次方程组的应用,关键是根据已知先列出二元一次方程组求出、的值,根据图示列出算式以及关于、的二元一次方程组.
第1页,共1页
同课章节目录
