人教版数学八年级上册 第十三章 轴对称:13.1.1 轴对称课件(23张PPT)
文档属性
| 名称 | 人教版数学八年级上册 第十三章 轴对称:13.1.1 轴对称课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 22:03:25 | ||
图片预览







文档简介
(共23张PPT)
第十三章 轴对称
13.1.1轴对称
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
对称现象无处不在,从自然景观到艺术作品,从建筑物到交通标志,甚至日常生活用品,都可以找到对称的例子,对称给我们带来美的感受!
你还能举出生活中见到的对称现象吗?
新课导入
讲授新知
贰
同学们又举出了下列实例,仔细观察,你能从这些图片中得到什么规律?
归 纳
以上图形沿着一条直线翻折后,直线两旁的两个部分能够完全重合.
从这节课开始我们就一起来学习这类特殊的图形的有关性质.
讲授新知
概念: 如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
此时,也说这个图形关于这条直线(成轴)对称.
(1)轴对称图形是对一个图形来讲的,它是一个图形自身的对称特征,它被对称轴分成的两部分能够互相重合.
(2)一个轴对称图形的对称轴可以有一条,也可以有多条.
知识点1 轴对称的图形
讲授新知
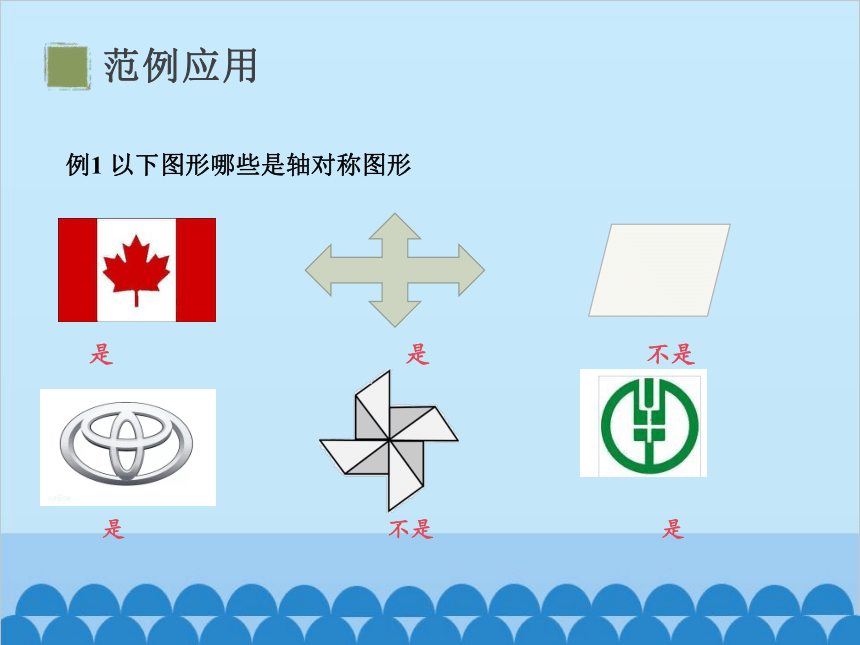
例1 以下图形哪些是轴对称图形
是 是 不是
是 不是 是
范例应用
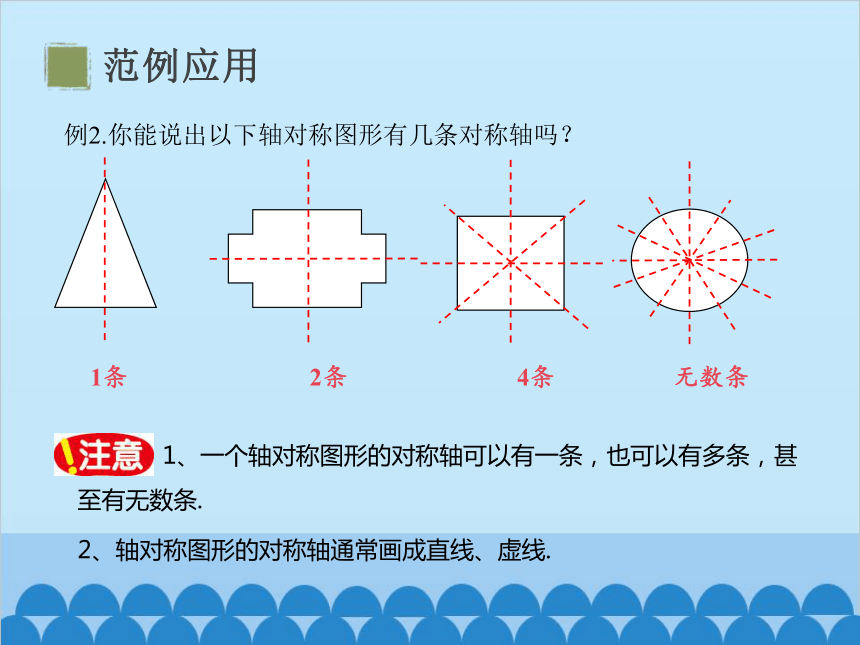
例2.你能说出以下轴对称图形有几条对称轴吗?
1条 2条 4条 无数条
1、一个轴对称图形的对称轴可以有一条,也可以有多条,甚至有无数条.
2、轴对称图形的对称轴通常画成直线、虚线.
范例应用
同学们仔细观察,下列每对图片有什么共同特点?
图中的每一对图形沿着虚线折叠,左边的图形能够和右边的图形重合.
归 纳
知识点2 轴对称
讲授新知
轴对称:把一个图形沿着某一条直线折叠,如果它能够与另外一个图形重合,那么就说这两个图形关于这条直线(成轴)对称.这条直线叫做对称轴,折叠后能够重合的点是对应点,叫做对称点.
理解轴对称定义的三点:1.有两个图形;2.存在一条直线;3.使得一个图形沿着这条直线折叠后与另外一个图形重合.
讲授新知
例3 分别观察以下每组图形,判断它们是否关于某条直线成轴对称?
是 不是 是
不是 不是 是
E
E
E
E
E
E
E
E
E
E
E
E
范例应用
比较归纳
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
讲授新知
如图所示,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
知识点2 轴对称的性质
讲授新知
如图,MN⊥AA′, AP=A′P.
直线MN是线段AA ′的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
图形轴对称的性质
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
线段的垂直平分线
讲授新知
例4.如图,△ABC和△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB//DF
B.∠B=∠E
C.AB=DE
D.AD的连线被直线MN垂直平分
A
B
C
D
E
F
M
N
A
△ABC≌△DEF
点A与点D是对称点
范例应用
当堂训练
叁
当堂训练
1.下面四个汉字中,是轴对称图形的是( )
A.书 B.香 C.宜 D.昌
2.下列各组图形中,成轴对称的两个图形是( )
3.完成下列填空:
(1)成轴对称的两个图形的对应角____,对应边____.
(2)在“线段、钝角、长方形、等边三角形”这四个图形中,是轴对称图形的有___个,其中对称轴最多的是__________,线段的对称轴是___________.
(3)成轴对称的两个图形___全等形;把一个轴对称图形沿着对称轴分成两个图形,这两个图形___全等形.(填“是”或“否”)
D
C
相等
相等
4
等边三角形
经过线段中点且垂直于这条直线
是
是
4. 下面的图形是否是轴对称图形,如果是,有几条对称轴?画画看.
课堂小结
肆
轴对称
轴对称图形
两个图形成轴对称
垂直平分线
区别
联系
课堂小结
课后作业
基础题:1.课后练习 P60第 1,2题。
提高题:2.请学有余力的同学P64 T2,3,4
谢
谢
第十三章 轴对称
13.1.1轴对称
新课导入
壹
目
录
课堂小结
肆
当堂训练
叁
讲授新知
贰
新课导入
壹
对称现象无处不在,从自然景观到艺术作品,从建筑物到交通标志,甚至日常生活用品,都可以找到对称的例子,对称给我们带来美的感受!
你还能举出生活中见到的对称现象吗?
新课导入
讲授新知
贰
同学们又举出了下列实例,仔细观察,你能从这些图片中得到什么规律?
归 纳
以上图形沿着一条直线翻折后,直线两旁的两个部分能够完全重合.
从这节课开始我们就一起来学习这类特殊的图形的有关性质.
讲授新知
概念: 如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
此时,也说这个图形关于这条直线(成轴)对称.
(1)轴对称图形是对一个图形来讲的,它是一个图形自身的对称特征,它被对称轴分成的两部分能够互相重合.
(2)一个轴对称图形的对称轴可以有一条,也可以有多条.
知识点1 轴对称的图形
讲授新知
例1 以下图形哪些是轴对称图形
是 是 不是
是 不是 是
范例应用
例2.你能说出以下轴对称图形有几条对称轴吗?
1条 2条 4条 无数条
1、一个轴对称图形的对称轴可以有一条,也可以有多条,甚至有无数条.
2、轴对称图形的对称轴通常画成直线、虚线.
范例应用
同学们仔细观察,下列每对图片有什么共同特点?
图中的每一对图形沿着虚线折叠,左边的图形能够和右边的图形重合.
归 纳
知识点2 轴对称
讲授新知
轴对称:把一个图形沿着某一条直线折叠,如果它能够与另外一个图形重合,那么就说这两个图形关于这条直线(成轴)对称.这条直线叫做对称轴,折叠后能够重合的点是对应点,叫做对称点.
理解轴对称定义的三点:1.有两个图形;2.存在一条直线;3.使得一个图形沿着这条直线折叠后与另外一个图形重合.
讲授新知
例3 分别观察以下每组图形,判断它们是否关于某条直线成轴对称?
是 不是 是
不是 不是 是
E
E
E
E
E
E
E
E
E
E
E
E
范例应用
比较归纳
轴对称图形 两个图形成轴对称
图形
区别
联系
一个图形具有的特殊形状
两个全等图形的特殊的位置关系
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
讲授新知
如图所示,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
知识点2 轴对称的性质
讲授新知
如图,MN⊥AA′, AP=A′P.
直线MN是线段AA ′的垂直平分线.
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
图形轴对称的性质
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
线段的垂直平分线
讲授新知
例4.如图,△ABC和△DEF关于直线MN对称,则以下结论中错误的是( )
A.AB//DF
B.∠B=∠E
C.AB=DE
D.AD的连线被直线MN垂直平分
A
B
C
D
E
F
M
N
A
△ABC≌△DEF
点A与点D是对称点
范例应用
当堂训练
叁
当堂训练
1.下面四个汉字中,是轴对称图形的是( )
A.书 B.香 C.宜 D.昌
2.下列各组图形中,成轴对称的两个图形是( )
3.完成下列填空:
(1)成轴对称的两个图形的对应角____,对应边____.
(2)在“线段、钝角、长方形、等边三角形”这四个图形中,是轴对称图形的有___个,其中对称轴最多的是__________,线段的对称轴是___________.
(3)成轴对称的两个图形___全等形;把一个轴对称图形沿着对称轴分成两个图形,这两个图形___全等形.(填“是”或“否”)
D
C
相等
相等
4
等边三角形
经过线段中点且垂直于这条直线
是
是
4. 下面的图形是否是轴对称图形,如果是,有几条对称轴?画画看.
课堂小结
肆
轴对称
轴对称图形
两个图形成轴对称
垂直平分线
区别
联系
课堂小结
课后作业
基础题:1.课后练习 P60第 1,2题。
提高题:2.请学有余力的同学P64 T2,3,4
谢
谢
