2022-2023学年黑龙江省哈尔滨市南岗区重点中学七年级(下)期末数学试卷(五四学制)(含解析)
文档属性
| 名称 | 2022-2023学年黑龙江省哈尔滨市南岗区重点中学七年级(下)期末数学试卷(五四学制)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 414.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 20:56:17 | ||
图片预览



文档简介
2022-2023学年黑龙江省哈尔滨市南岗区重点中学七年级(下)期末数学试卷(五四学制)
一、选择题(本大题共6小题,共18.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
2. 已知,则下列不等式一定成立的是( )
A. B. C. D.
3. 下列四个图形中,线段是的高的图形是( )
A. B.
C. D.
4. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,某校调查了一个班名学生每天的睡眠时间,绘成睡眠时间条形统计图如图所示,则所调查学生睡眠时间的平均数和中位数分别为( )
A. ,
B. ,
C. ,
D. ,
5. 如图,已知为边延长线上一点,于交于,,,则的度数为( )
A.
B.
C.
D.
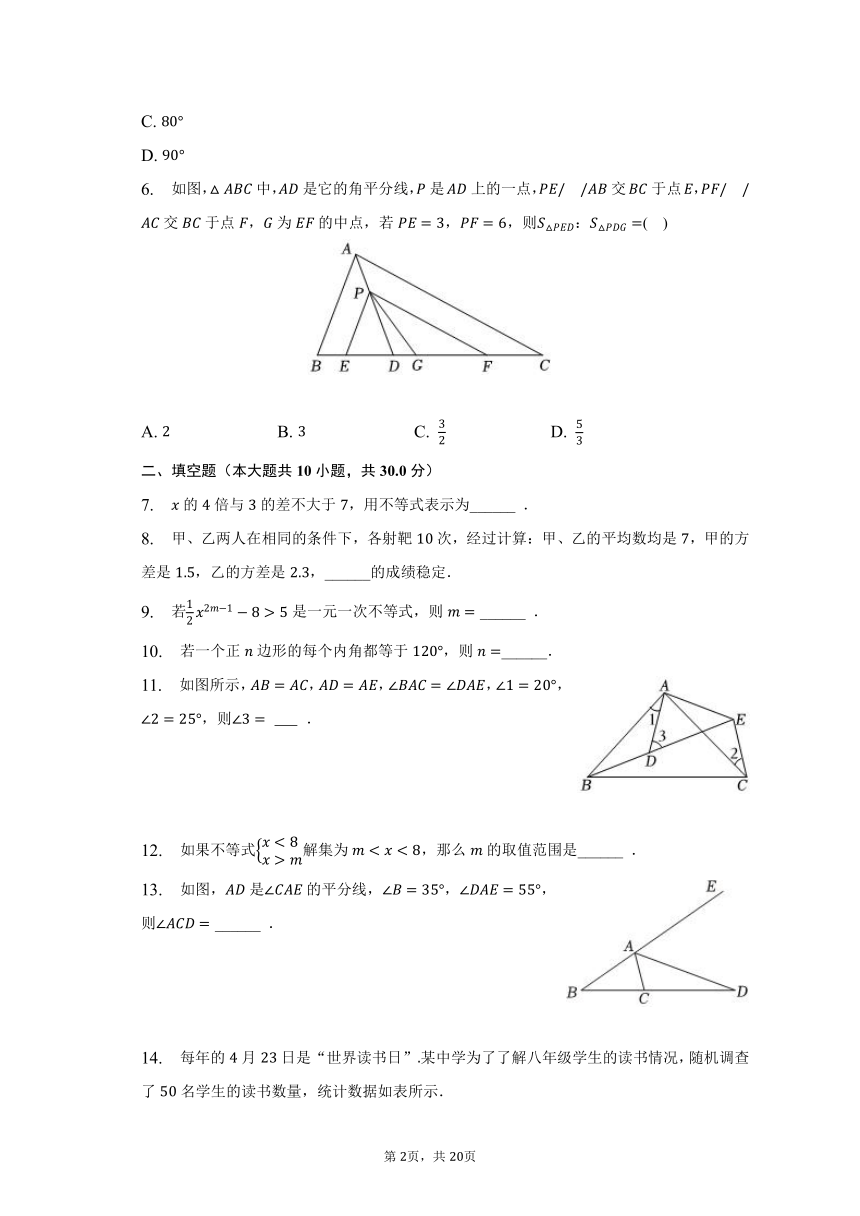
6. 如图,中,是它的角平分线,是上的一点,交于点,交于点,为的中点,若,,则:( )
A. B. C. D.
二、填空题(本大题共10小题,共30.0分)
7. 的倍与的差不大于,用不等式表示为______ .
8. 甲、乙两人在相同的条件下,各射靶次,经过计算:甲、乙的平均数均是,甲的方差是,乙的方差是,______的成绩稳定.
9. 若是一元一次不等式,则 ______ .
10. 若一个正边形的每个内角都等于,则______.
11. 如图所示,,,,,,则 .
12. 如果不等式解集为,那么的取值范围是______ .
13. 如图,是的平分线,,,则 ______ .
14. 每年的月日是“世界读书日”某中学为了了解八年级学生的读书情况,随机调查了名学生的读书数量,统计数据如表所示.
数量册
人数
在这组统计数据中,若将这名学生读书册数的众数记为,中位数记为,则 ______ .
15. 已知为的高线,为角平分线,当,时,______度.
16. 在等边三角形中,点是线段上一点,点是线段上一点,与交于点,,,::,则______
三、计算题(本大题共1小题,共8.0分)
17. 一个被墨水污染了的方程组:,小明回忆道:“这个方程组的解是,而我求的解是,经检验后发现,我的错误是由于看错了第二个方程中的系数所致”根据小明的回忆,你能求出原方程组吗?
四、解答题(本大题共8小题,共64.0分。解答应写出文字说明,证明过程或演算步骤)
18. 本小题分
解下列方程组:
;
.
19. 本小题分
解不等式组.
解不等式
解不等式组
20. 本小题分
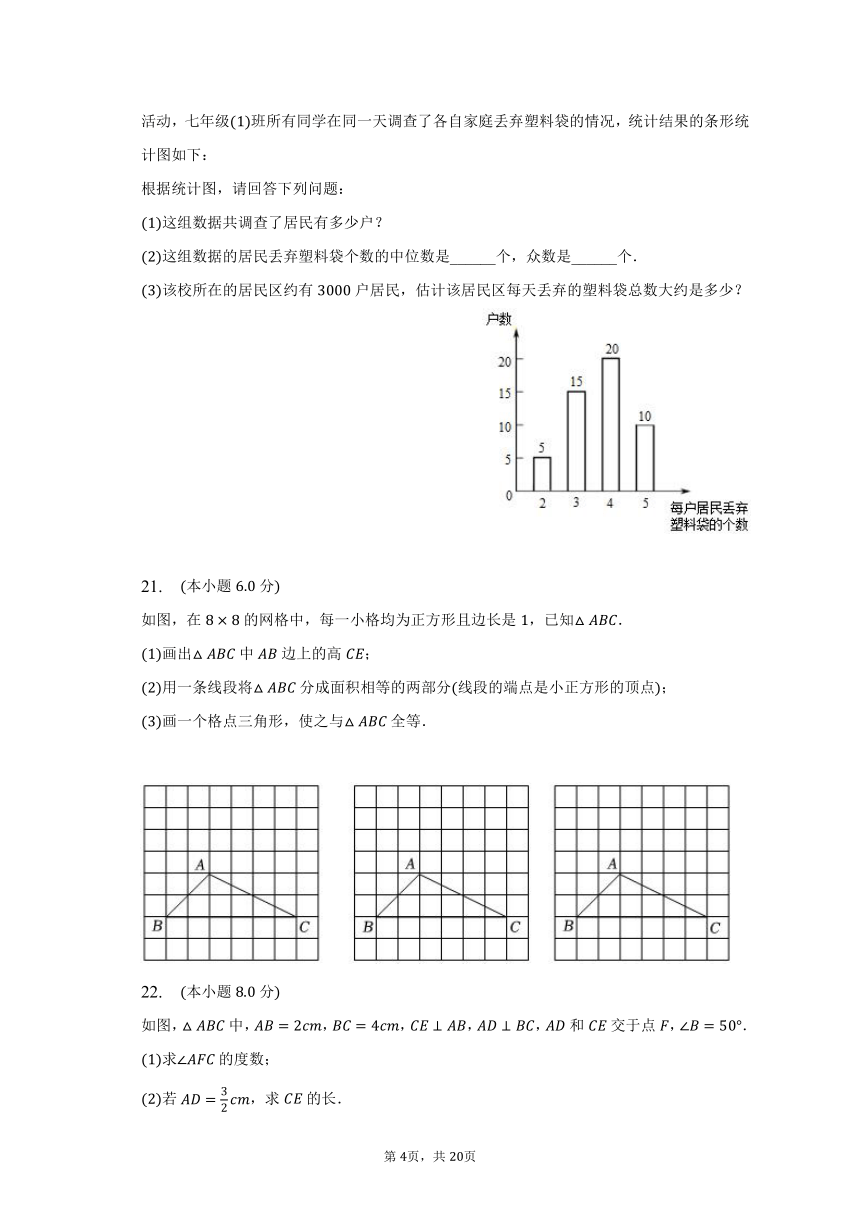
为保护环境,增强居民环保意识,某校积极参加即将到来的月日的“世界环境日”宣传活动,七年级班所有同学在同一天调查了各自家庭丢弃塑料袋的情况,统计结果的条形统计图如下:
根据统计图,请回答下列问题:
这组数据共调查了居民有多少户?
这组数据的居民丢弃塑料袋个数的中位数是______个,众数是______个.
该校所在的居民区约有户居民,估计该居民区每天丢弃的塑料袋总数大约是多少?
21. 本小题分
如图,在的网格中,每一小格均为正方形且边长是,已知.
画出中边上的高;
用一条线段将分成面积相等的两部分线段的端点是小正方形的顶点;
画一个格点三角形,使之与全等.
22. 本小题分
如图,中,,,,,和交于点,.
求的度数;
若,求的长.
23. 本小题分
阅读以下例题:解不等式:.
解:当,则,
即可以写成:,解不等式组得:.
.
当若,则,
即可以写成:,解不等式组得:.
.
综合以上两种情况:原不等式的解集为:或.
以上解法的依据为:当,则同号.
请你模仿例题的解法,解不等式:
;
.
24. 本小题分
某机械厂甲、乙两个生产车间承担生产同一种零件的任务.甲、乙两车间共有人,甲车间平均每人每天生产零件个,乙车间平均每人每天生产零件个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为个.
求甲、乙两车间各有多少人?
该机械厂改进了生产技术,在甲、乙两车间总人数不变的情况下,从甲车间调出一部分人到乙车间,调整后甲车间平均每人每天生产零件个,乙车间平均每人每天生产零件个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于个,求从甲车间最多调出多少人到乙车间?
25. 本小题分
在四边形中,,.
如图,连接,求证:;
如图,在的延长线上取一点,连接,在上取一点,连接,当时,求证:;
如图,在条件下,平分交于点,连接,当,时,求的长.
答案和解析
1.【答案】
【解析】解:、方程组中含有两个未知数,的次数为,不符合题意;
B、方程组中含有三个未知数,不符合题意;
C、方程组中含有两个未知数,每个未知数的次数为,符合题意;
D、方程组中含有两个未知数,中未知数的次数为,不符合题意.
故选:.
根据二元一次方程组的定义,含有两个未知数,且含有的未知数的项的次数为,逐一进行判断即可.
本题考查了二元一次方程组的定义,熟练掌握含有两个未知数,且含有的未知数的项的次数为的方程是解题的关键.
2.【答案】
【解析】解:、,设,,则,
故A不符合题意;
B、,
,
故B不符合题意;
C、,
,
故C不符合题意;
D、,
,
故D符合题意;
故选:.
根据不等式的性质,进行计算即可解答.
本题考查了不等式的性质,熟练掌握不等式的性质是解题的关键.
3.【答案】
【解析】
【分析】
本题主要考查了三角形的高,三角形的高是指从三角形的一个顶点向对边作垂线,连接顶点与垂足之间的线段.熟记定义是解题的关键.
根据三角形高的画法知,过点作边上的高,垂足为,其中线段是的高,再结合图形进行判断.
【解答】
解:线段是的高的图是选项A.
故选A.
4.【答案】
【解析】解:所调查学生睡眠时间的平均数为;
共有名学生,中位数是从小到大排列后第、个数的平均数,
所调查学生睡眠时间的中位数是.
故选:.
直接利用加权平均数以及中位数的概念分别分析求出即可.
本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.也考查了平均数与中位数的概念.
5.【答案】
【解析】解:,
,
,
,
,
.
故选:.
由垂直可得,从而可求得,由对顶角相等得,即可求的度数.
本题主要考查三角形的内角和定理,解答的关键是熟记三角形的内角和为.
6.【答案】
【解析】解法一:如图,作交于点,则,
是的角平分线,
,
交于点,交于点,
,,
,
,
,
,,,
,
∽,
,
,
,
设,则,,
为的中点,
,
,
,即:,
故选:.
解法二:如图,作于点,于点,于点,
是的角平分线,
,
交于点,交于点,
,,
,
,
,
,,
,
设,则,,
为的中点,
,
,
,即:,
故选:.
由交于点,交于点,得,,因为,所以,然后再求与的比,有两种方法,方法一是作交于点,可证明,则,再证明∽,得,则,方法二是作于点,于点,于点,则,由,求得,设,则,,,所以,即可求得,于是得到问题的答案.
此题重点考查角平分线的性质、平行线的性质、等腰三角形的判定、平行线分线段成比例定理、相似三角形的判定与性质、根据面积等式求线段的比等知识与方法,正确地作出所需要的辅助线是解题的关键.
7.【答案】
【解析】解:由题意得:.
故答案为:.
首先表示的倍与的差为,再表示不大于可得不等式.
此题主要考查了由实际问题抽象出一元一次不等式,关键是要抓住题目中的关键词,如“大于小于、不超过不低于、是正数负数”“至少”、“最多”等等,正确选择不等号.
8.【答案】甲
【解析】解:甲、乙的平均数均是,甲的方差是,乙的方差是,
而,
成绩比较稳定的是甲.
故答案为:甲.
根据方差的定义,方差越小数据越稳定即可求解.
本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
9.【答案】
【解析】解:根据题意,解得.
故答案为:.
根据一元一次不等式的定义,,求解即可.
本题考查一元一次不等式定义的“未知数的最高次数为次”这一条件.
10.【答案】
【解析】多边形的内角和可以表示成,因为所给多边形的每个内角均相等,故又可表示成,列方程可求解.此题还可以由已知条件,求出这个多边形的外角,再利用多边形的外角和定理求解.
解:解法一:设所求正边形边数为,
则,
解得;
解法二:设所求正边形边数为,
正边形的每个内角都等于,
正边形的每个外角都等于.
又因为多边形的外角和为,
即,
.
本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
11.【答案】
【解析】解:,
,
即,
在与中,
,
≌,
,
.
故答案为:.
根据等式的性质得出,再利用全等三角形的判定和性质解答即可.
此题考查全等三角形的判定和性质,关键是根据等式的性质得出.
12.【答案】
【解析】解:不等式组解集为,
.
故答案为:.
根据“大小小大中间找”的原则进行解答即可.
本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的法则是解答此题的关键.
13.【答案】
【解析】解:由三角形的外角性质得,,
是的平分线,
,
.
故答案为:.
根据三角形的一个外角等于与它不相邻的两个内角的和可得,根据角平分线的定义可得,然后利用三角形的内角和定理列式计算即可得解.
本题考查了三角形的一个外角等于与它不相邻的两个内角的和,三角形的内角和定理,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.
14.【答案】
【解析】解:这组样本数据中,出现了次,出现的次数最多,
这组数据的众数是.
将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是,
这组数据的中位数为,
.
故答案为:.
在这组样本数据中,出现的次数最多,所以求出了众数,将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是,从而求出中位数是,再代入计算即可.
本题考查了众数以及中位数的知识,解题的关键是牢记概念.
15.【答案】
【解析】解:,,
,
为角平分线,
,
为的高,
,
,
,
故答案为:.
根据三角形的内角和定理求出的度数,再根据是的角平分线,求出的度数,则的度数可求出.
本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是三角形的内角和定理.
16.【答案】
【解析】解:是等边三角形,
,,
,
≌,
,
::,
可以假设:,则,
,
,
,
,
,
,
,
故答案为.
由≌,推出,由题意可以假设,则,由,可得,由此构建方程求出即可解决问题;
本题考查全等三角形的判定和性质、等边三角形的性质、三角形内角和定理等知识,解题的关键是正确寻找全等三角形解决问题,学会利用参数构建方程解决问题.
17.【答案】解:设正确的方程组为:,
这个方程组的解是,
,
,
又他的错误是由于看错了第二个方程中的系数所致,
,
解之得:,,
原方程组为:.
【解析】设方程组中的系数分别为,,,由于这个方程组的解是,而小明求的解是,由此可以得到、、方程组,解方程组即可求解.
此题主要考查了二元一次方程的解的应用,解题的关键是利用方程的解的定义得到的待定系数的方程组解决问题.
18.【答案】解:,
得:,
解得:,
把代入得:,
解得:,
所以,原方程组的解为:;
,
得:,
解得:,
把代入得:,
解得:,
所以,原方程组的解为:.
【解析】用加减消元法解方程组;
用加减消元法解方程组.
本题考查二元一次方程组的解法,熟练掌握加减消元是解题的关键.
19.【答案】解:,
,
,
,
,
;
,
解得;
解得.
故不等式组的解集为.
【解析】去分母;去括号;移项;合并同类项;化系数为.
解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分.
考查了解一元一次不等式组,方法与步骤:求不等式组中每个不等式的解集;利用数轴求公共部分.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
20.【答案】
【解析】解:这组数据共调查了居民有户;
这组数据的居民丢弃塑料袋个数的中位数是个,众数是个,
故答案为:,;
个,
答:该居民区每天丢弃的塑料袋总数大约是个.
根据题意列式计算即可;
根据中位数和众数的定义即可得到结论;
乘以这组数据的平均数即可得到结论.
本题考查了条形统计图,众数和中位数的定义,正确的理解题意是解题的关键.
21.【答案】解:如图中,线段即为所求;
如图中,线段即为所求答案不唯一;
如图中,即为所求答案不唯一
【解析】根据三角形的高的第一年画出图形;
作出的中线即可;
根据全等三角形的判定方法,画出图形即可.
本题考查作图应用与设计作图,三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
22.【答案】解:,
,
在中,,
,
,
,
,
,
在中,;
,,
,
,
,,,
,
.
【解析】根据,求出即可.
利用面积法求解即可.
本题考查三角形的面积,三角形的外角的性质等知识,解题的关键是学会利用面积法求高,属于中考常考题型.
23.【答案】解:当,则,
即可以写成:,解不等式组的解集,
,则,
即可以写成:,解不等式组的解集,
两种情况:不等式组的解集:或;
当,则,
即可以写成:,解不等式组无解;
当,则,
即可以写成:,解不等式组得:,
综合以上两种情况:不等式组解集:,
【解析】仿照例题的思路,分两种情况,进行计算即可解答;
仿照例题的思路,分两种情况,进行计算即可解答.
本题考查了解一元一次不等式组,熟练掌握解一元一次不等式组的步骤是解题的关键.
24.【答案】解:设甲车间有人,乙车间有人,由题意得,
,
解得:,
答:甲车间有人,乙车间有人.
设从甲车间调出人到乙车间,则甲车间有人,乙车间有人,
解得:
答:从甲车间最多调出人到乙车间.
【解析】设甲、乙两车间各有、人,根据甲、乙两车间共有人和甲车间每天生产零件总数与乙车间每天生产零件总数之和为个列方程组成方程组解决问题;
设从甲车间调出人到乙车间,表示出两个车间的人数,根据生产零件总数之和不少于个,列出不等式求得即可.
此题主要考查了二元一次方程组的应用以及不等式的应用,根据已知得出正确的不等式关系是解题关键.
25.【答案】解:证明:在与中,,
≌,
,
;
,,
,
,
;
延长交于,
平分交于点,
,
,
,
在与中,,
≌,
,,
,
,
在与中,,
≌,
,
,
,
,
,
,
.
【解析】根据全等三角形的性质得到,
根据平行线的判定定理即可得到;
根据三角形的外角的性质和等腰三角形的性质即可得到结论;
延长交于,根据全等三角形的性质得到,,根据平行线的性质得到,由全等三角形的性质得到,等量代换即可得到结论.
本题考查了平行四边形的判定和性质,全等三角形的判定和性质,等腰三角形的判定和性质,三角形的外角的性质,正确的作出辅助线构造全等三角形是解题的关键.
第1页,共1页
一、选择题(本大题共6小题,共18.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列方程组中,是二元一次方程组的是( )
A. B.
C. D.
2. 已知,则下列不等式一定成立的是( )
A. B. C. D.
3. 下列四个图形中,线段是的高的图形是( )
A. B.
C. D.
4. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求,了解学生的睡眠状况,某校调查了一个班名学生每天的睡眠时间,绘成睡眠时间条形统计图如图所示,则所调查学生睡眠时间的平均数和中位数分别为( )
A. ,
B. ,
C. ,
D. ,
5. 如图,已知为边延长线上一点,于交于,,,则的度数为( )
A.
B.
C.
D.
6. 如图,中,是它的角平分线,是上的一点,交于点,交于点,为的中点,若,,则:( )
A. B. C. D.
二、填空题(本大题共10小题,共30.0分)
7. 的倍与的差不大于,用不等式表示为______ .
8. 甲、乙两人在相同的条件下,各射靶次,经过计算:甲、乙的平均数均是,甲的方差是,乙的方差是,______的成绩稳定.
9. 若是一元一次不等式,则 ______ .
10. 若一个正边形的每个内角都等于,则______.
11. 如图所示,,,,,,则 .
12. 如果不等式解集为,那么的取值范围是______ .
13. 如图,是的平分线,,,则 ______ .
14. 每年的月日是“世界读书日”某中学为了了解八年级学生的读书情况,随机调查了名学生的读书数量,统计数据如表所示.
数量册
人数
在这组统计数据中,若将这名学生读书册数的众数记为,中位数记为,则 ______ .
15. 已知为的高线,为角平分线,当,时,______度.
16. 在等边三角形中,点是线段上一点,点是线段上一点,与交于点,,,::,则______
三、计算题(本大题共1小题,共8.0分)
17. 一个被墨水污染了的方程组:,小明回忆道:“这个方程组的解是,而我求的解是,经检验后发现,我的错误是由于看错了第二个方程中的系数所致”根据小明的回忆,你能求出原方程组吗?
四、解答题(本大题共8小题,共64.0分。解答应写出文字说明,证明过程或演算步骤)
18. 本小题分
解下列方程组:
;
.
19. 本小题分
解不等式组.
解不等式
解不等式组
20. 本小题分
为保护环境,增强居民环保意识,某校积极参加即将到来的月日的“世界环境日”宣传活动,七年级班所有同学在同一天调查了各自家庭丢弃塑料袋的情况,统计结果的条形统计图如下:
根据统计图,请回答下列问题:
这组数据共调查了居民有多少户?
这组数据的居民丢弃塑料袋个数的中位数是______个,众数是______个.
该校所在的居民区约有户居民,估计该居民区每天丢弃的塑料袋总数大约是多少?
21. 本小题分
如图,在的网格中,每一小格均为正方形且边长是,已知.
画出中边上的高;
用一条线段将分成面积相等的两部分线段的端点是小正方形的顶点;
画一个格点三角形,使之与全等.
22. 本小题分
如图,中,,,,,和交于点,.
求的度数;
若,求的长.
23. 本小题分
阅读以下例题:解不等式:.
解:当,则,
即可以写成:,解不等式组得:.
.
当若,则,
即可以写成:,解不等式组得:.
.
综合以上两种情况:原不等式的解集为:或.
以上解法的依据为:当,则同号.
请你模仿例题的解法,解不等式:
;
.
24. 本小题分
某机械厂甲、乙两个生产车间承担生产同一种零件的任务.甲、乙两车间共有人,甲车间平均每人每天生产零件个,乙车间平均每人每天生产零件个,甲车间每天生产零件总数与乙车间每天生产零件总数之和为个.
求甲、乙两车间各有多少人?
该机械厂改进了生产技术,在甲、乙两车间总人数不变的情况下,从甲车间调出一部分人到乙车间,调整后甲车间平均每人每天生产零件个,乙车间平均每人每天生产零件个,若甲车间每天生产零件总数与乙车间每天生产零件总数之和不少于个,求从甲车间最多调出多少人到乙车间?
25. 本小题分
在四边形中,,.
如图,连接,求证:;
如图,在的延长线上取一点,连接,在上取一点,连接,当时,求证:;
如图,在条件下,平分交于点,连接,当,时,求的长.
答案和解析
1.【答案】
【解析】解:、方程组中含有两个未知数,的次数为,不符合题意;
B、方程组中含有三个未知数,不符合题意;
C、方程组中含有两个未知数,每个未知数的次数为,符合题意;
D、方程组中含有两个未知数,中未知数的次数为,不符合题意.
故选:.
根据二元一次方程组的定义,含有两个未知数,且含有的未知数的项的次数为,逐一进行判断即可.
本题考查了二元一次方程组的定义,熟练掌握含有两个未知数,且含有的未知数的项的次数为的方程是解题的关键.
2.【答案】
【解析】解:、,设,,则,
故A不符合题意;
B、,
,
故B不符合题意;
C、,
,
故C不符合题意;
D、,
,
故D符合题意;
故选:.
根据不等式的性质,进行计算即可解答.
本题考查了不等式的性质,熟练掌握不等式的性质是解题的关键.
3.【答案】
【解析】
【分析】
本题主要考查了三角形的高,三角形的高是指从三角形的一个顶点向对边作垂线,连接顶点与垂足之间的线段.熟记定义是解题的关键.
根据三角形高的画法知,过点作边上的高,垂足为,其中线段是的高,再结合图形进行判断.
【解答】
解:线段是的高的图是选项A.
故选A.
4.【答案】
【解析】解:所调查学生睡眠时间的平均数为;
共有名学生,中位数是从小到大排列后第、个数的平均数,
所调查学生睡眠时间的中位数是.
故选:.
直接利用加权平均数以及中位数的概念分别分析求出即可.
本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.也考查了平均数与中位数的概念.
5.【答案】
【解析】解:,
,
,
,
,
.
故选:.
由垂直可得,从而可求得,由对顶角相等得,即可求的度数.
本题主要考查三角形的内角和定理,解答的关键是熟记三角形的内角和为.
6.【答案】
【解析】解法一:如图,作交于点,则,
是的角平分线,
,
交于点,交于点,
,,
,
,
,
,,,
,
∽,
,
,
,
设,则,,
为的中点,
,
,
,即:,
故选:.
解法二:如图,作于点,于点,于点,
是的角平分线,
,
交于点,交于点,
,,
,
,
,
,,
,
设,则,,
为的中点,
,
,
,即:,
故选:.
由交于点,交于点,得,,因为,所以,然后再求与的比,有两种方法,方法一是作交于点,可证明,则,再证明∽,得,则,方法二是作于点,于点,于点,则,由,求得,设,则,,,所以,即可求得,于是得到问题的答案.
此题重点考查角平分线的性质、平行线的性质、等腰三角形的判定、平行线分线段成比例定理、相似三角形的判定与性质、根据面积等式求线段的比等知识与方法,正确地作出所需要的辅助线是解题的关键.
7.【答案】
【解析】解:由题意得:.
故答案为:.
首先表示的倍与的差为,再表示不大于可得不等式.
此题主要考查了由实际问题抽象出一元一次不等式,关键是要抓住题目中的关键词,如“大于小于、不超过不低于、是正数负数”“至少”、“最多”等等,正确选择不等号.
8.【答案】甲
【解析】解:甲、乙的平均数均是,甲的方差是,乙的方差是,
而,
成绩比较稳定的是甲.
故答案为:甲.
根据方差的定义,方差越小数据越稳定即可求解.
本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
9.【答案】
【解析】解:根据题意,解得.
故答案为:.
根据一元一次不等式的定义,,求解即可.
本题考查一元一次不等式定义的“未知数的最高次数为次”这一条件.
10.【答案】
【解析】多边形的内角和可以表示成,因为所给多边形的每个内角均相等,故又可表示成,列方程可求解.此题还可以由已知条件,求出这个多边形的外角,再利用多边形的外角和定理求解.
解:解法一:设所求正边形边数为,
则,
解得;
解法二:设所求正边形边数为,
正边形的每个内角都等于,
正边形的每个外角都等于.
又因为多边形的外角和为,
即,
.
本题考查根据多边形的内角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.
11.【答案】
【解析】解:,
,
即,
在与中,
,
≌,
,
.
故答案为:.
根据等式的性质得出,再利用全等三角形的判定和性质解答即可.
此题考查全等三角形的判定和性质,关键是根据等式的性质得出.
12.【答案】
【解析】解:不等式组解集为,
.
故答案为:.
根据“大小小大中间找”的原则进行解答即可.
本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的法则是解答此题的关键.
13.【答案】
【解析】解:由三角形的外角性质得,,
是的平分线,
,
.
故答案为:.
根据三角形的一个外角等于与它不相邻的两个内角的和可得,根据角平分线的定义可得,然后利用三角形的内角和定理列式计算即可得解.
本题考查了三角形的一个外角等于与它不相邻的两个内角的和,三角形的内角和定理,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.
14.【答案】
【解析】解:这组样本数据中,出现了次,出现的次数最多,
这组数据的众数是.
将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是,
这组数据的中位数为,
.
故答案为:.
在这组样本数据中,出现的次数最多,所以求出了众数,将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是,从而求出中位数是,再代入计算即可.
本题考查了众数以及中位数的知识,解题的关键是牢记概念.
15.【答案】
【解析】解:,,
,
为角平分线,
,
为的高,
,
,
,
故答案为:.
根据三角形的内角和定理求出的度数,再根据是的角平分线,求出的度数,则的度数可求出.
本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是三角形的内角和定理.
16.【答案】
【解析】解:是等边三角形,
,,
,
≌,
,
::,
可以假设:,则,
,
,
,
,
,
,
,
故答案为.
由≌,推出,由题意可以假设,则,由,可得,由此构建方程求出即可解决问题;
本题考查全等三角形的判定和性质、等边三角形的性质、三角形内角和定理等知识,解题的关键是正确寻找全等三角形解决问题,学会利用参数构建方程解决问题.
17.【答案】解:设正确的方程组为:,
这个方程组的解是,
,
,
又他的错误是由于看错了第二个方程中的系数所致,
,
解之得:,,
原方程组为:.
【解析】设方程组中的系数分别为,,,由于这个方程组的解是,而小明求的解是,由此可以得到、、方程组,解方程组即可求解.
此题主要考查了二元一次方程的解的应用,解题的关键是利用方程的解的定义得到的待定系数的方程组解决问题.
18.【答案】解:,
得:,
解得:,
把代入得:,
解得:,
所以,原方程组的解为:;
,
得:,
解得:,
把代入得:,
解得:,
所以,原方程组的解为:.
【解析】用加减消元法解方程组;
用加减消元法解方程组.
本题考查二元一次方程组的解法,熟练掌握加减消元是解题的关键.
19.【答案】解:,
,
,
,
,
;
,
解得;
解得.
故不等式组的解集为.
【解析】去分母;去括号;移项;合并同类项;化系数为.
解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分.
考查了解一元一次不等式组,方法与步骤:求不等式组中每个不等式的解集;利用数轴求公共部分.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.
20.【答案】
【解析】解:这组数据共调查了居民有户;
这组数据的居民丢弃塑料袋个数的中位数是个,众数是个,
故答案为:,;
个,
答:该居民区每天丢弃的塑料袋总数大约是个.
根据题意列式计算即可;
根据中位数和众数的定义即可得到结论;
乘以这组数据的平均数即可得到结论.
本题考查了条形统计图,众数和中位数的定义,正确的理解题意是解题的关键.
21.【答案】解:如图中,线段即为所求;
如图中,线段即为所求答案不唯一;
如图中,即为所求答案不唯一
【解析】根据三角形的高的第一年画出图形;
作出的中线即可;
根据全等三角形的判定方法,画出图形即可.
本题考查作图应用与设计作图,三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
22.【答案】解:,
,
在中,,
,
,
,
,
,
在中,;
,,
,
,
,,,
,
.
【解析】根据,求出即可.
利用面积法求解即可.
本题考查三角形的面积,三角形的外角的性质等知识,解题的关键是学会利用面积法求高,属于中考常考题型.
23.【答案】解:当,则,
即可以写成:,解不等式组的解集,
,则,
即可以写成:,解不等式组的解集,
两种情况:不等式组的解集:或;
当,则,
即可以写成:,解不等式组无解;
当,则,
即可以写成:,解不等式组得:,
综合以上两种情况:不等式组解集:,
【解析】仿照例题的思路,分两种情况,进行计算即可解答;
仿照例题的思路,分两种情况,进行计算即可解答.
本题考查了解一元一次不等式组,熟练掌握解一元一次不等式组的步骤是解题的关键.
24.【答案】解:设甲车间有人,乙车间有人,由题意得,
,
解得:,
答:甲车间有人,乙车间有人.
设从甲车间调出人到乙车间,则甲车间有人,乙车间有人,
解得:
答:从甲车间最多调出人到乙车间.
【解析】设甲、乙两车间各有、人,根据甲、乙两车间共有人和甲车间每天生产零件总数与乙车间每天生产零件总数之和为个列方程组成方程组解决问题;
设从甲车间调出人到乙车间,表示出两个车间的人数,根据生产零件总数之和不少于个,列出不等式求得即可.
此题主要考查了二元一次方程组的应用以及不等式的应用,根据已知得出正确的不等式关系是解题关键.
25.【答案】解:证明:在与中,,
≌,
,
;
,,
,
,
;
延长交于,
平分交于点,
,
,
,
在与中,,
≌,
,,
,
,
在与中,,
≌,
,
,
,
,
,
,
.
【解析】根据全等三角形的性质得到,
根据平行线的判定定理即可得到;
根据三角形的外角的性质和等腰三角形的性质即可得到结论;
延长交于,根据全等三角形的性质得到,,根据平行线的性质得到,由全等三角形的性质得到,等量代换即可得到结论.
本题考查了平行四边形的判定和性质,全等三角形的判定和性质,等腰三角形的判定和性质,三角形的外角的性质,正确的作出辅助线构造全等三角形是解题的关键.
第1页,共1页
同课章节目录
