八年级数学下册试题6.4 多边形的内角和与外角和同步练习-北师大版(含答案)
文档属性
| 名称 | 八年级数学下册试题6.4 多边形的内角和与外角和同步练习-北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 619.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 21:54:55 | ||
图片预览


文档简介
6.4 多边形的内角和与外角和
一、单选题
1.若多边形的边数由5增加到n(n为大于5的正整数),则其外角和的度数( )
A.增加 B.减少 C.不变 D.不能确定
2.下列多边形中,内角和为360°的图形是( )
A. B. C. D.
3.三角形的外角和度数是( )
A.180° B.270° C.360° D.720°
4.若一个正多边形的内角和等于其外角和的3倍,则这个正多边形是( )
A.5边形 B.6边形 C.7边形 D.8边形
5.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是,这个多边形的边数是( )
A.6 B.8 C.9 D.10
6.正八边形一个内角是( )度
A.45 B.135 C.112.5 D.108
7.一个多边形的每个内角都相等,已知它的一个外角为20°,那么这个多边形是一个( )
A.正十八边形 B.正十六边形 C.正十四边形 D.正十二边形
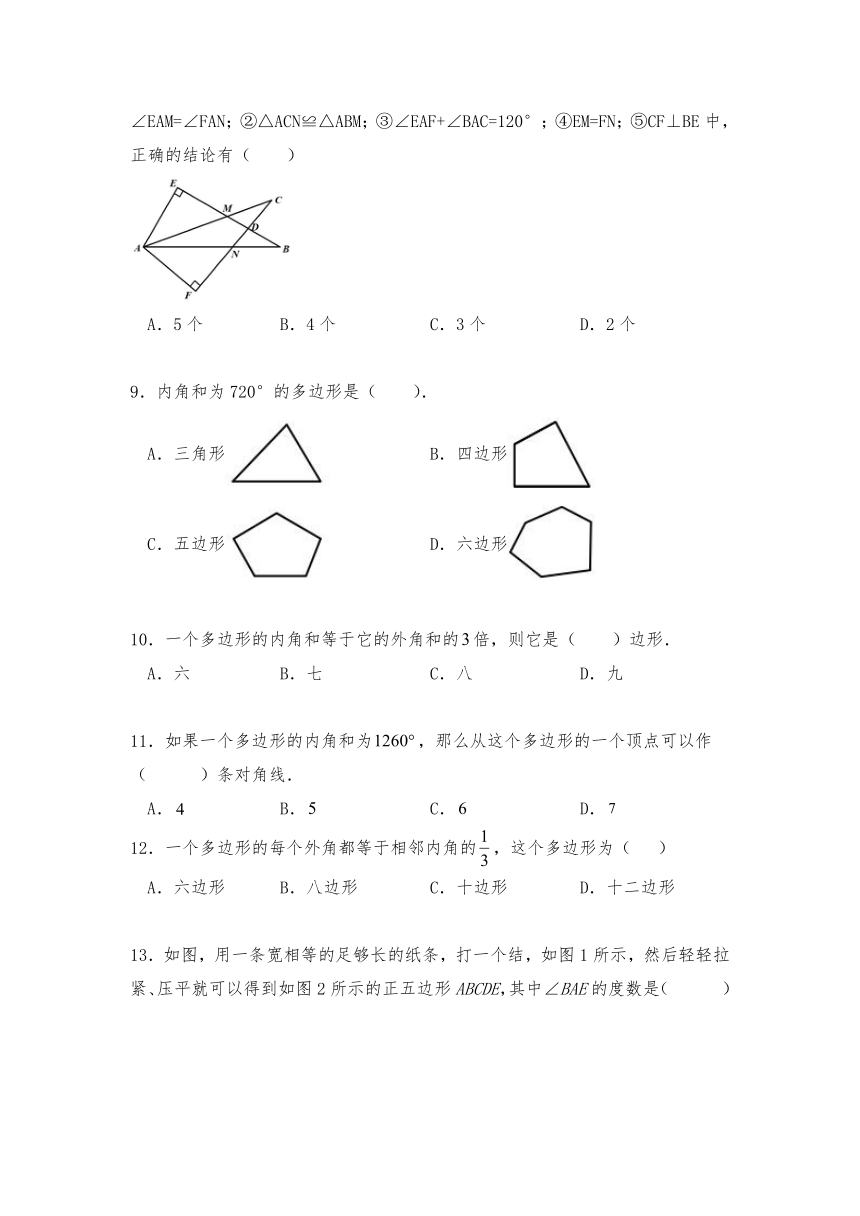
8.如图,将两块大小相同的三角板(∠B=∠C=30°的直角三角形)按图中所示的位置摆放.若BE交CF于点D交AC于点M,AB交CF于点N,则下列结论:①∠EAM=∠FAN;②△ACN≌△ABM;③∠EAF+∠BAC=120°;④EM=FN;⑤CF⊥BE中,正确的结论有( )
A.5个 B.4个 C.3个 D.2个
9.内角和为720°的多边形是( ).
A.三角形 B.四边形
C.五边形 D.六边形
10.一个多边形的内角和等于它的外角和的倍,则它是( )边形.
A.六 B.七 C.八 D.九
11.如果一个多边形的内角和为,那么从这个多边形的一个顶点可以作( )条对角线.
A. B. C. D.
12.一个多边形的每个外角都等于相邻内角的,这个多边形为( )
A.六边形 B.八边形 C.十边形 D.十二边形
13.如图,用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE,其中∠BAE的度数是( )
A.90° B.108° C.120° D.135°
14.一个多边形的内角和外角和之比为4:1,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
15.在△ABC中,高BD和CE所在的直线相交于点O,且点O与点B、C不重合,∠A=50°,则∠BOC的度数为( ).
A.50°或130° B.40°或130° C.50°或65 D.40°或65°
16.如图,在中,,沿图中虚线截去,则( )
A.288 B.252 C.180 D.144
17.五边形ABCDE中,、、、对应的邻补角和等于215°,则的度数为( )
A.30° B.35° C.40° D.45°
18.在计算一个多边形内角和时,多加了一个角,得到的内角和为1500°,那么原多边形的边数为( )
A.9 B.10 C.11 D.10或11
19.若过边形的一个顶点的所有对角线正好将该边形分成个三角形,则的值是( )
A. B. C. D.
二、填空题
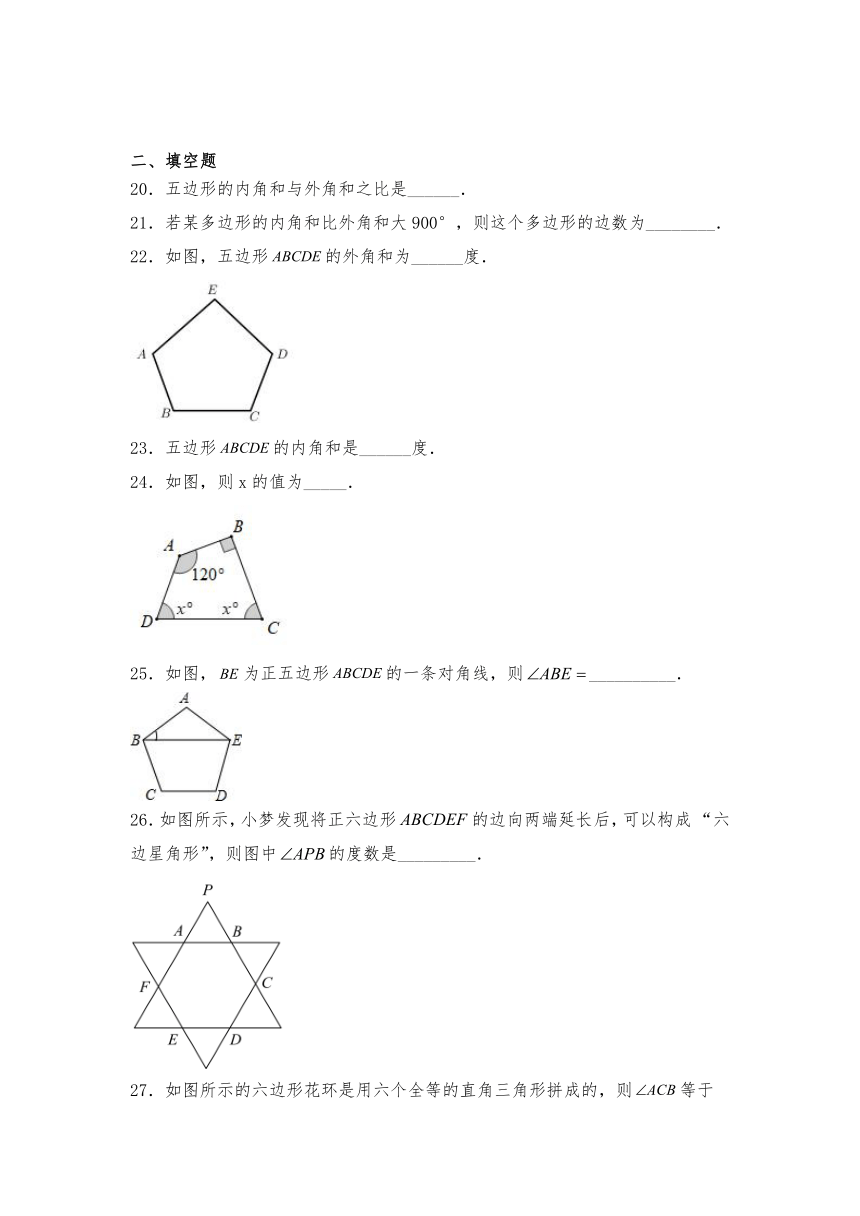
20.五边形的内角和与外角和之比是______.
21.若某多边形的内角和比外角和大900°,则这个多边形的边数为________.
22.如图,五边形的外角和为______度.
23.五边形的内角和是______度.
24.如图,则x的值为_____.
25.如图,为正五边形的一条对角线,则__________.
26.如图所示,小梦发现将正六边形的边向两端延长后,可以构成 “六边星角形”,则图中的度数是_________.
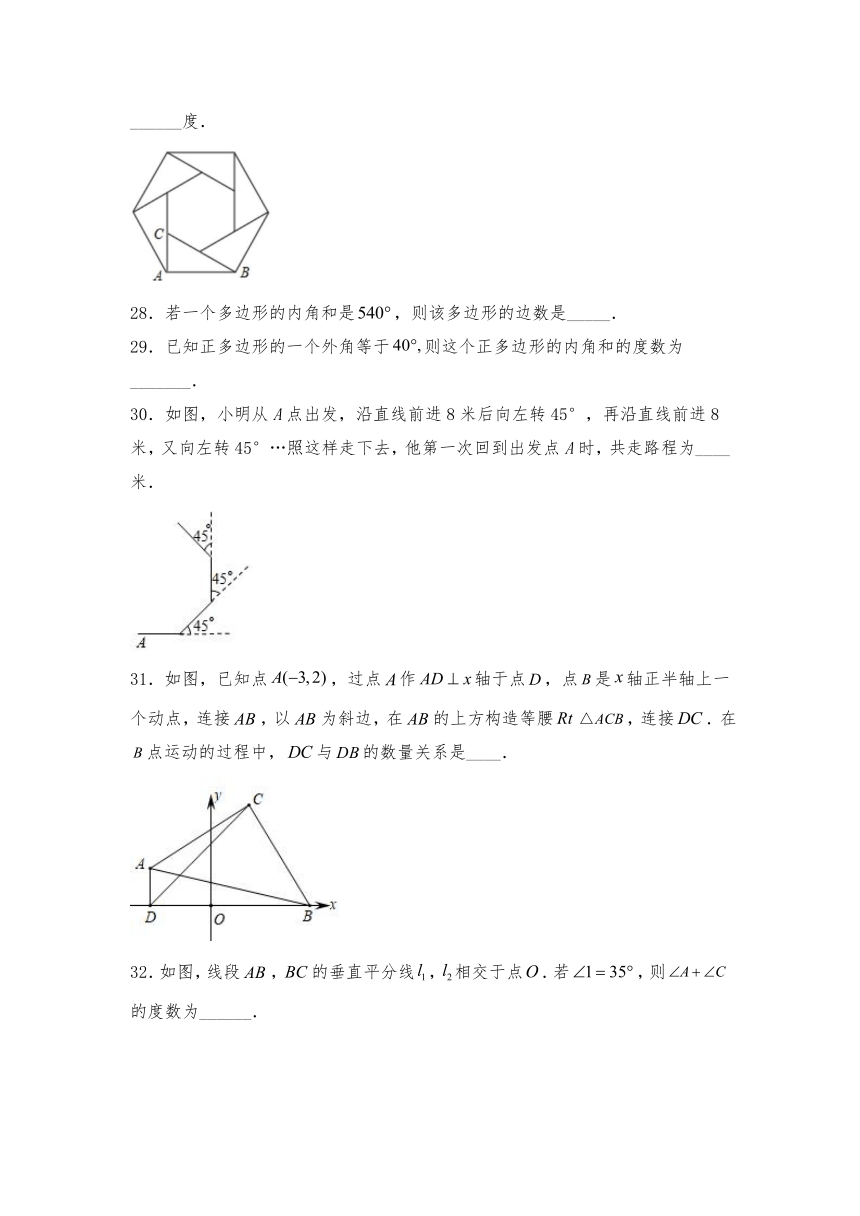
27.如图所示的六边形花环是用六个全等的直角三角形拼成的,则等于______度.
28.若一个多边形的内角和是,则该多边形的边数是_____.
29.已知正多边形的一个外角等于则这个正多边形的内角和的度数为_______.
30.如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为____米.
31.如图,已知点,过点作轴于点,点是轴正半轴上一个动点,连接,以为斜边,在的上方构造等腰,连接.在点运动的过程中,与的数量关系是____.
32.如图,线段,的垂直平分线,相交于点.若,则的度数为______.
33.多边形每一个内角都等于108°,多边形一个顶点可引的对角线的条数是________条.
34.将正三角形、正四边形、正五边形按如图所示的位置摆放.如果,,那么 __________.
35.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为___________.
36.如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则________.
37.如图,在一个四边形ABCD中,AE平分∠BAD,DE平分∠ADC,且∠ABC=80°,∠BCD=70°,则∠AED=_________.
38.如图,六边形ABCDEF中,AB∥DC,∠1、∠2、∠3、∠4分别是∠BAF、∠AFE、∠FED、∠EDC的外角,则∠1+∠2+∠3+∠4=_____.
三、解答题
39.如图,为内部一点,、分别为点关于直线、对称的点.
(1)若,求的度数;
(2)试猜想当的值最大时,与需要满足什么数量关系,并说明理由.
40.(1)一个多边形的内角和比它的外角和多,求该多边形的边数;
(2)如图,已知是的角平分线,是的高,与相交于点F,,,求和的度数.
41.(1)如图1,在△ABC中,已知OB,OC分别平分∠ABC,∠ACB,BP,CP分别平分∠ABC,∠ACB,的外角∠DBC,∠ECB.
①若∠A=50 ,则∠O=______,∠P=______;
②若∠A=α,则∠O=______,∠P=______.(用含α的式子表示)
(2)如图2,在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,请探究∠P与∠A,∠D的数量关系,并说明理由;
(3)如图3,在六边形ABCDEF中,CP,DP分别平分外角∠GCD,∠HDC,请直接写出∠P与∠A,∠B,∠E,∠F的数量关系______.
42.如图,在中.是边上一点,平分是上一点,是边上一点.且.
(1)若,直接写出的度数(用含的式子表示).
(2)求证:.
43.在平面中,我们把大于且小于的角称为优角.如果两个角相加等于,那么称这两个角互为组角,简称互组.
(1)若,互为组角,且,则______.
习惯上,我们把有一个内角大于的四边形俗称为镖形.
(2)如图,在镖形ABCD中,优角与钝角互为组角,试探索内角,∠B,与钝角之间的数量关系,并至少用两种以上的方法说明理由.
44.已知在四边形ABCD中,.
(1)如图1,若BE平分,DF平分的邻补角,请写出BE与DF的位置关系并证明;
(2)如图2,若BF、DE分别平分、的邻补角,判断DE与BF位置关系并证明;
(3)如图3,若BE、DE分别五等分、的邻补角(即),求度数.
答案
一、单选题
C.B.C.D.D.B.A.B.D.C.C.B.B.D.A.B.B.B.D
二、填空题
20.3:2
21.9
22.360
23.540
24.75
25.36°
26.60°
27.60
28.5
29.1260°.
30.64
31.
32.35°
33.2
34.35°
35.360°
36.10°
37.75°.
38.180°
三、解答题
39.(1)如图,连接OP、OR、PR,分别交AB、BC与点E、F,
、分别为点关于直线、对称的点,
,
,
,
;
(2)如图1,连接PB、BR、PR,易知,
如图2,当P、B、R三点共线时,PR有最大值=PB+BR,
P、B、R三点共线,
P、O、R构成三角形,
、分别为点关于直线、对称的点,
OB=BP,OB=BR,,
,,
,
,
,
,
,
,
当的值最大时,与需要满足.
40.
解:(1)设该多边形的边数为n,由已知,得
,
解得,
∴该多边形的边数为8;
(2)∵是的角平分线,且,
∴,,
又∵,
∴,
∵是的高,
∴,
∴.
41.
解:(1)①连结AO并延长到Q,连结PA
∵OB,OC分别平分∠ABC,∠ACB,
∴∠ABO=;∠ACO=,
∴∠BOQ=∠ABO+∠BAO,∠QOC=∠OCA+∠OAC,
∴∠BOC=∠BOQ+∠QOC=∠ABO+∠BAO+∠OCA+∠OAC,
∴∠BOC=∠BAC++,
=∠A++,
=∠A+180°- ,
=90°+,
=115°,
BP,CP分别平分∠ABC,∠ACB的外角∠DBC,∠ECB,
∴∠DBP=;∠ECP=,
∠DBP=∠BAP+∠BPA,∠ECP=∠CAP+∠CPA,
∴∠DBP+∠ECP=∠BAP+∠BPA+∠CAP+∠CPA=∠A+∠P,
∴,
∴,
∴90 +,
∴,
故答案为:115 ;65 ;
②由①得∠O=90°+, ,
∵∠A=α,
∴∠O=90°+,,
故答案为:∠O=90°+,,
解:,
理由如下:
在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,
∴∠CBP=;∠BCP=,
,
,
,
,
;
(3)延长CB,DE交直线AF与M、N如图,
由(2)得,
∴∠M=∠FAB+∠CBA-180 ,∠N=∠EFA+∠DEF-180 ,
∴∠M+∠N=∠FAB+∠CBA-180 +∠EFA+∠DEF-180 =∠FAB+∠CBA+∠EFA+∠DEF-360 ,
∴,
∴,
∴,
故答案为:.
42.解:(1)在四边形ABPQ中,
∴
∵
∴
(2)连接PC
∵AB=AC,平分
∴AD垂直平分BC
∵P是AD上一点
∴PB=PC
在△ABP和△ACP中
∴△ABP≌△ACP(SSS)
∴∠ABP=∠ACP
又由(1)已证
∴
∴PQ=PC
∴PB=PQ
43.
解:(1)∵∠1、∠2互为组角,且∠1=135°,
∴∠2=360°-∠1=225°,
故答案为:225°;
(2)钝角∠BCD=∠A+∠B+∠D.
理由如下:
理由①:∵在四边形ABCD中,∠A+∠B+优角∠BCD+∠D=360°,
又∵优角∠BCD+钝角∠BCD=360° ,
∴钝角∠BCD=∠A+∠B+∠D;
理由②:如下图,连接AC并延长,
∵∠BAC+∠B=∠BCE,∠DAC+∠D=∠DCE(三角形外角的性质),
∴钝角∠BCD=∠BCE+∠DCE=∠BAC+∠B+∠DAC+∠D=∠A+∠B+∠D.
44.(1).
证明:延长BE、FD交于G.在四边形ABCD中,
,,
.
,.
平分,DF平分,
,,
,
∵∠ABE+∠AEB=90°,∠AEB=∠DEG,∠FDN=∠EDG,
∴∠DEG+∠EDG=90°,
∴∠EGD=90°,即BE⊥DF.
(2).
证明:连接DB.
,.
又,.
、DF平分、的邻补角,
,,
.
在中,
,
,
,.
(3)延长DC交BE于H.由(1)得:
.
、DE分别五等分、的邻补角,
,
由三角形的外角性质得,
,,
,
.
一、单选题
1.若多边形的边数由5增加到n(n为大于5的正整数),则其外角和的度数( )
A.增加 B.减少 C.不变 D.不能确定
2.下列多边形中,内角和为360°的图形是( )
A. B. C. D.
3.三角形的外角和度数是( )
A.180° B.270° C.360° D.720°
4.若一个正多边形的内角和等于其外角和的3倍,则这个正多边形是( )
A.5边形 B.6边形 C.7边形 D.8边形
5.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是,这个多边形的边数是( )
A.6 B.8 C.9 D.10
6.正八边形一个内角是( )度
A.45 B.135 C.112.5 D.108
7.一个多边形的每个内角都相等,已知它的一个外角为20°,那么这个多边形是一个( )
A.正十八边形 B.正十六边形 C.正十四边形 D.正十二边形
8.如图,将两块大小相同的三角板(∠B=∠C=30°的直角三角形)按图中所示的位置摆放.若BE交CF于点D交AC于点M,AB交CF于点N,则下列结论:①∠EAM=∠FAN;②△ACN≌△ABM;③∠EAF+∠BAC=120°;④EM=FN;⑤CF⊥BE中,正确的结论有( )
A.5个 B.4个 C.3个 D.2个
9.内角和为720°的多边形是( ).
A.三角形 B.四边形
C.五边形 D.六边形
10.一个多边形的内角和等于它的外角和的倍,则它是( )边形.
A.六 B.七 C.八 D.九
11.如果一个多边形的内角和为,那么从这个多边形的一个顶点可以作( )条对角线.
A. B. C. D.
12.一个多边形的每个外角都等于相邻内角的,这个多边形为( )
A.六边形 B.八边形 C.十边形 D.十二边形
13.如图,用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE,其中∠BAE的度数是( )
A.90° B.108° C.120° D.135°
14.一个多边形的内角和外角和之比为4:1,则这个多边形的边数是( )
A.7 B.8 C.9 D.10
15.在△ABC中,高BD和CE所在的直线相交于点O,且点O与点B、C不重合,∠A=50°,则∠BOC的度数为( ).
A.50°或130° B.40°或130° C.50°或65 D.40°或65°
16.如图,在中,,沿图中虚线截去,则( )
A.288 B.252 C.180 D.144
17.五边形ABCDE中,、、、对应的邻补角和等于215°,则的度数为( )
A.30° B.35° C.40° D.45°
18.在计算一个多边形内角和时,多加了一个角,得到的内角和为1500°,那么原多边形的边数为( )
A.9 B.10 C.11 D.10或11
19.若过边形的一个顶点的所有对角线正好将该边形分成个三角形,则的值是( )
A. B. C. D.
二、填空题
20.五边形的内角和与外角和之比是______.
21.若某多边形的内角和比外角和大900°,则这个多边形的边数为________.
22.如图,五边形的外角和为______度.
23.五边形的内角和是______度.
24.如图,则x的值为_____.
25.如图,为正五边形的一条对角线,则__________.
26.如图所示,小梦发现将正六边形的边向两端延长后,可以构成 “六边星角形”,则图中的度数是_________.
27.如图所示的六边形花环是用六个全等的直角三角形拼成的,则等于______度.
28.若一个多边形的内角和是,则该多边形的边数是_____.
29.已知正多边形的一个外角等于则这个正多边形的内角和的度数为_______.
30.如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为____米.
31.如图,已知点,过点作轴于点,点是轴正半轴上一个动点,连接,以为斜边,在的上方构造等腰,连接.在点运动的过程中,与的数量关系是____.
32.如图,线段,的垂直平分线,相交于点.若,则的度数为______.
33.多边形每一个内角都等于108°,多边形一个顶点可引的对角线的条数是________条.
34.将正三角形、正四边形、正五边形按如图所示的位置摆放.如果,,那么 __________.
35.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数为___________.
36.如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则________.
37.如图,在一个四边形ABCD中,AE平分∠BAD,DE平分∠ADC,且∠ABC=80°,∠BCD=70°,则∠AED=_________.
38.如图,六边形ABCDEF中,AB∥DC,∠1、∠2、∠3、∠4分别是∠BAF、∠AFE、∠FED、∠EDC的外角,则∠1+∠2+∠3+∠4=_____.
三、解答题
39.如图,为内部一点,、分别为点关于直线、对称的点.
(1)若,求的度数;
(2)试猜想当的值最大时,与需要满足什么数量关系,并说明理由.
40.(1)一个多边形的内角和比它的外角和多,求该多边形的边数;
(2)如图,已知是的角平分线,是的高,与相交于点F,,,求和的度数.
41.(1)如图1,在△ABC中,已知OB,OC分别平分∠ABC,∠ACB,BP,CP分别平分∠ABC,∠ACB,的外角∠DBC,∠ECB.
①若∠A=50 ,则∠O=______,∠P=______;
②若∠A=α,则∠O=______,∠P=______.(用含α的式子表示)
(2)如图2,在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,请探究∠P与∠A,∠D的数量关系,并说明理由;
(3)如图3,在六边形ABCDEF中,CP,DP分别平分外角∠GCD,∠HDC,请直接写出∠P与∠A,∠B,∠E,∠F的数量关系______.
42.如图,在中.是边上一点,平分是上一点,是边上一点.且.
(1)若,直接写出的度数(用含的式子表示).
(2)求证:.
43.在平面中,我们把大于且小于的角称为优角.如果两个角相加等于,那么称这两个角互为组角,简称互组.
(1)若,互为组角,且,则______.
习惯上,我们把有一个内角大于的四边形俗称为镖形.
(2)如图,在镖形ABCD中,优角与钝角互为组角,试探索内角,∠B,与钝角之间的数量关系,并至少用两种以上的方法说明理由.
44.已知在四边形ABCD中,.
(1)如图1,若BE平分,DF平分的邻补角,请写出BE与DF的位置关系并证明;
(2)如图2,若BF、DE分别平分、的邻补角,判断DE与BF位置关系并证明;
(3)如图3,若BE、DE分别五等分、的邻补角(即),求度数.
答案
一、单选题
C.B.C.D.D.B.A.B.D.C.C.B.B.D.A.B.B.B.D
二、填空题
20.3:2
21.9
22.360
23.540
24.75
25.36°
26.60°
27.60
28.5
29.1260°.
30.64
31.
32.35°
33.2
34.35°
35.360°
36.10°
37.75°.
38.180°
三、解答题
39.(1)如图,连接OP、OR、PR,分别交AB、BC与点E、F,
、分别为点关于直线、对称的点,
,
,
,
;
(2)如图1,连接PB、BR、PR,易知,
如图2,当P、B、R三点共线时,PR有最大值=PB+BR,
P、B、R三点共线,
P、O、R构成三角形,
、分别为点关于直线、对称的点,
OB=BP,OB=BR,,
,,
,
,
,
,
,
,
当的值最大时,与需要满足.
40.
解:(1)设该多边形的边数为n,由已知,得
,
解得,
∴该多边形的边数为8;
(2)∵是的角平分线,且,
∴,,
又∵,
∴,
∵是的高,
∴,
∴.
41.
解:(1)①连结AO并延长到Q,连结PA
∵OB,OC分别平分∠ABC,∠ACB,
∴∠ABO=;∠ACO=,
∴∠BOQ=∠ABO+∠BAO,∠QOC=∠OCA+∠OAC,
∴∠BOC=∠BOQ+∠QOC=∠ABO+∠BAO+∠OCA+∠OAC,
∴∠BOC=∠BAC++,
=∠A++,
=∠A+180°- ,
=90°+,
=115°,
BP,CP分别平分∠ABC,∠ACB的外角∠DBC,∠ECB,
∴∠DBP=;∠ECP=,
∠DBP=∠BAP+∠BPA,∠ECP=∠CAP+∠CPA,
∴∠DBP+∠ECP=∠BAP+∠BPA+∠CAP+∠CPA=∠A+∠P,
∴,
∴,
∴90 +,
∴,
故答案为:115 ;65 ;
②由①得∠O=90°+, ,
∵∠A=α,
∴∠O=90°+,,
故答案为:∠O=90°+,,
解:,
理由如下:
在四边形ABCD中,BP,CP分别平分外角∠EBC,∠FCB,
∴∠CBP=;∠BCP=,
,
,
,
,
;
(3)延长CB,DE交直线AF与M、N如图,
由(2)得,
∴∠M=∠FAB+∠CBA-180 ,∠N=∠EFA+∠DEF-180 ,
∴∠M+∠N=∠FAB+∠CBA-180 +∠EFA+∠DEF-180 =∠FAB+∠CBA+∠EFA+∠DEF-360 ,
∴,
∴,
∴,
故答案为:.
42.解:(1)在四边形ABPQ中,
∴
∵
∴
(2)连接PC
∵AB=AC,平分
∴AD垂直平分BC
∵P是AD上一点
∴PB=PC
在△ABP和△ACP中
∴△ABP≌△ACP(SSS)
∴∠ABP=∠ACP
又由(1)已证
∴
∴PQ=PC
∴PB=PQ
43.
解:(1)∵∠1、∠2互为组角,且∠1=135°,
∴∠2=360°-∠1=225°,
故答案为:225°;
(2)钝角∠BCD=∠A+∠B+∠D.
理由如下:
理由①:∵在四边形ABCD中,∠A+∠B+优角∠BCD+∠D=360°,
又∵优角∠BCD+钝角∠BCD=360° ,
∴钝角∠BCD=∠A+∠B+∠D;
理由②:如下图,连接AC并延长,
∵∠BAC+∠B=∠BCE,∠DAC+∠D=∠DCE(三角形外角的性质),
∴钝角∠BCD=∠BCE+∠DCE=∠BAC+∠B+∠DAC+∠D=∠A+∠B+∠D.
44.(1).
证明:延长BE、FD交于G.在四边形ABCD中,
,,
.
,.
平分,DF平分,
,,
,
∵∠ABE+∠AEB=90°,∠AEB=∠DEG,∠FDN=∠EDG,
∴∠DEG+∠EDG=90°,
∴∠EGD=90°,即BE⊥DF.
(2).
证明:连接DB.
,.
又,.
、DF平分、的邻补角,
,,
.
在中,
,
,
,.
(3)延长DC交BE于H.由(1)得:
.
、DE分别五等分、的邻补角,
,
由三角形的外角性质得,
,,
,
.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
