等腰三角形的判定[上学期]
文档属性
| 名称 | 等腰三角形的判定[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 350.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-24 00:00:00 | ||
图片预览

文档简介
课件16张PPT。等腰三角形的判定新人教版八年级上册第十四章广西北海市第六中学
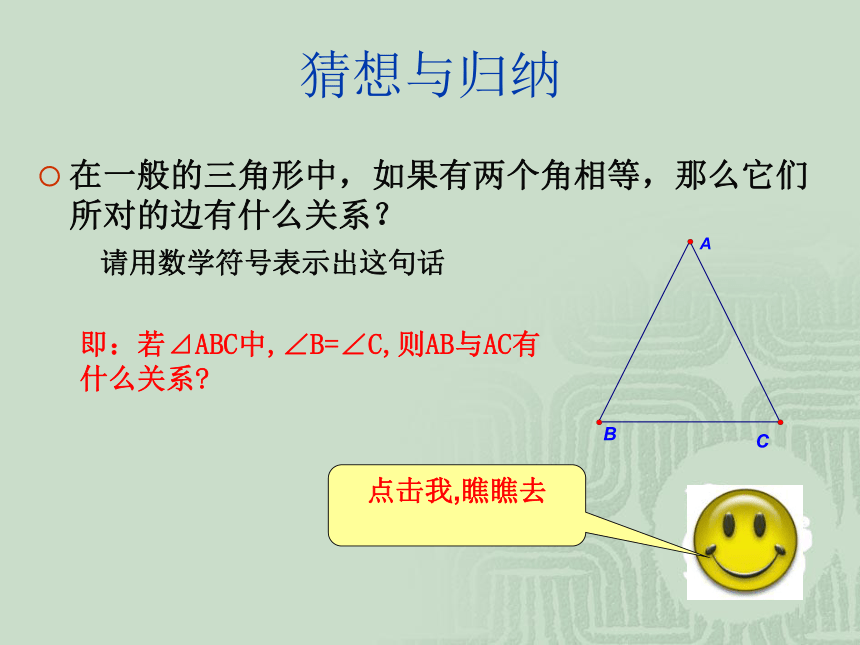
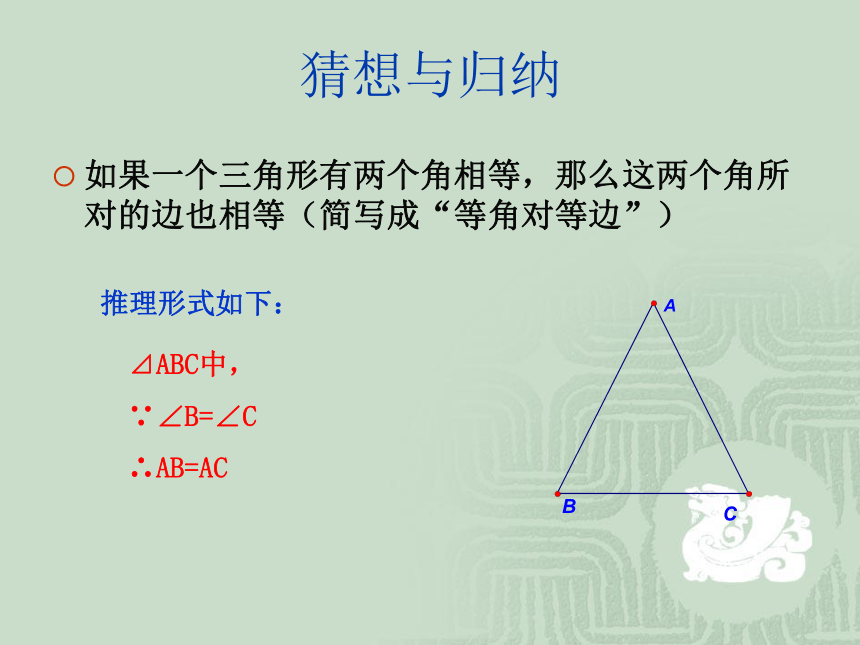
潘 康 林思考与探究如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A= ∠B。如果这两艘救生以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?ABOSOS!SOS!猜想与归纳在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?即:若⊿ABC中,∠B=∠C,则AB与AC有什么关系?点击我,瞧瞧去请用数学符号表示出这句话猜想与归纳如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)⊿ABC中,
∵∠B=∠C
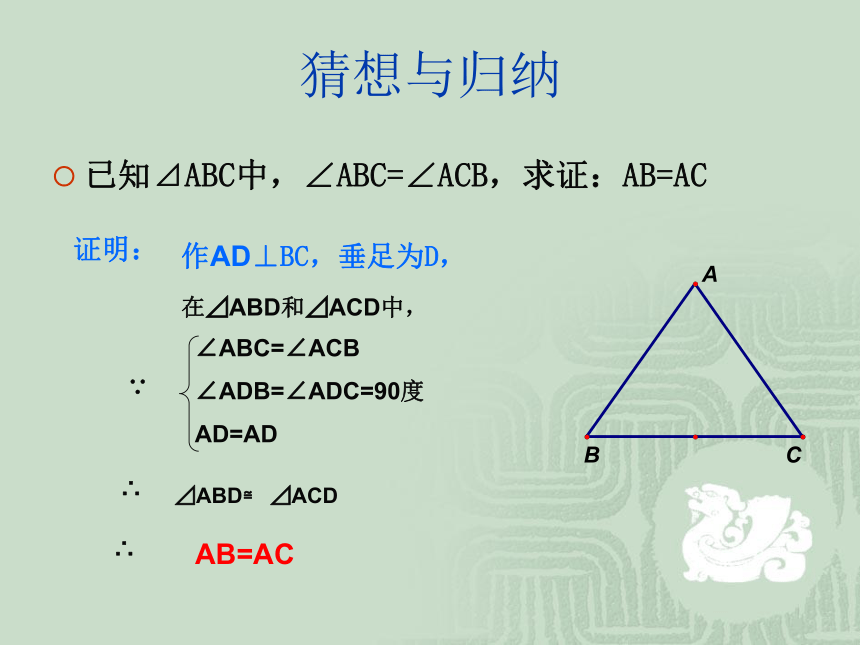
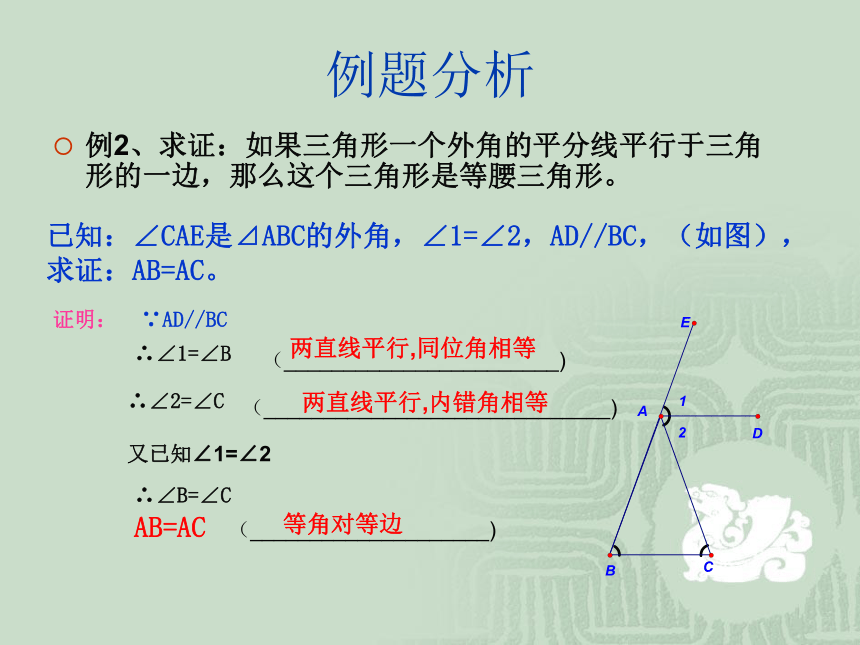
∴AB=AC推理形式如下:猜想与归纳已知⊿ABC中,∠ABC=∠ACB,求证:AB=AC证明:作AD⊥BC,垂足为D,在⊿ABD和⊿ACD中,⊿ABD≌ ⊿ACD∴例题分析例2、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
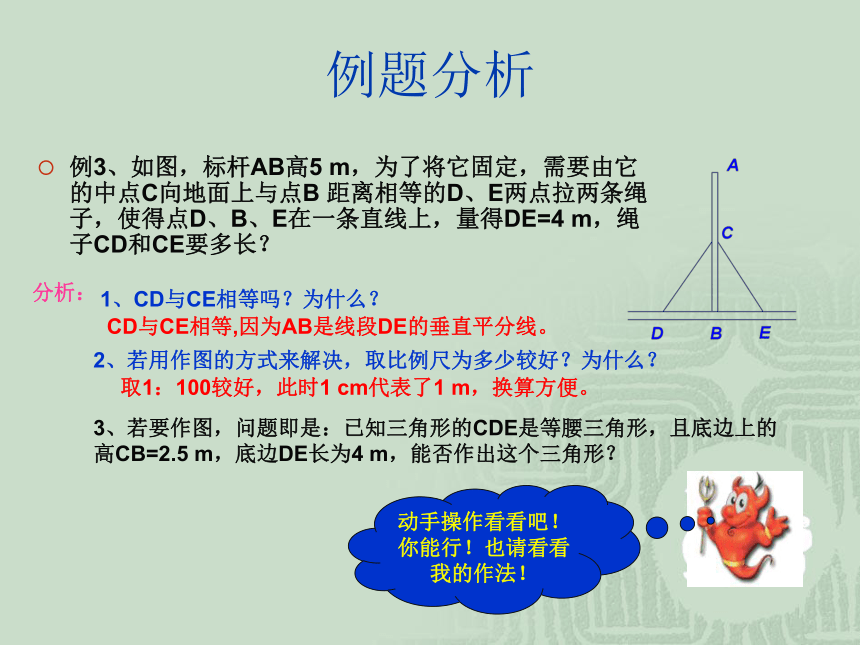
已知:∠CAE是⊿ABC的外角,∠1=∠2,AD//BC,(如图),求证:AB=AC。证明:∵AD//BC∴∠1=∠B∴∠2=∠C又已知∠1=∠2∴∠B=∠CAB=AC(_______________________)(_____________________________)(____________________)两直线平行,内错角相等等角对等边两直线平行,同位角相等例题分析例3、如图,标杆AB高5 m,为了将它固定,需要由它的中点C向地面上与点B 距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4 m,绳子CD和CE要多长?分析:1、CD与CE相等吗?为什么?2、若用作图的方式来解决,取比例尺为多少较好?为什么?3、若要作图,问题即是:已知三角形的CDE是等腰三角形,且底边上的高CB=2.5 m,底边DE长为4 m,能否作出这个三角形?动手操作看看吧!你能行!也请看看我的作法!CD与CE相等,因为AB是线段DE的垂直平分线。取1:100较好,此时1 cm代表了1 m,换算方便。练习1、如图,∠A=360,∠DBC=360,∠C=720,分别计算∠1、 ∠2的度数。答案:提示:∠1= 720,∠2=360由∠A=360,∠C=720得: ∠ABC=720在⊿ABC中∵ ∠DBC=360,∠1= ∠A+ ∠2 =360+360=720∴∠2=360练习2、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?ABCEDC答:重合部分是一个等腰三角形。∵由折叠可知∠ECD=∠EAB,∠C=∠A ,CD=AB,∴⊿EAB≌⊿ECD(AAS)∴EB=ED动画演示练习3、如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD。证明:∵ OA=OB∴∠OAB=∠0BA又∵ AB∥DC∴∠OCD=∠OAB
∠0DC =∠0BA(平行线的性质)∴∠OCD=∠ODC∴OC=OD生活应用上午八时,一条船从海岛A出发,以15海里的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得∠NAC=420,∠NBC=840,求从海岛B到灯塔C的距离。ABCN解:∵ ∠NBC=∠A+∠C(三角形的一个外角等于不相邻的两个内角的和)∴∠C= 840-420=420∴BA=BC(等角对等边)∵ AB=15(10-8)=30∴BC=BA=30(海里)思考拓展1、如图,⊿ABC中,BC=BA,∠A=600,BD是AC边的中线,延长BC到E,使CE=CD,求证:DE=DB提示:∵ BA=BC∴∠BCA=∠A=600(等边对等角)∵ CE=CD∴∠E=∠CDE=300(三角形外角性质)∵ BD是AC边的中线∴∠DBC=300(等腰三角形的性质)∴DE=DB(等角对等边)若DB是AC边上的高,上述结论还成立吗?若DB是AC边上的高,上述结论仍成立思考拓展1、如图,⊿ABC中,∠ABC、∠ACB的平分线交于点O,过点O作DE//BC,分别交AB、AC于点D、E,求证:BD+EC=DE提示:∵ DE//BC∴∠OBC=∠DOB,∠OCB=∠EOC∵ BO、CO分别平分∠ABC、∠ACB∴∠DBO=∠DOB=∠OBC,∠ECO=∠EOC=∠OCB∴BD=DO,CE=OE ∴BD+EC=DO+OE=DE(等角对等边)小结知识本节课你学到了等腰三角形的什么知识?
等角对等边可运用在什么方面?(证明两线段相等)作业课本:
P150 第十二题、第十三题再见著名的数学家,莫斯科大学教授雅洁卡提出:“解题就是把要解的题转化为已经解过的题”。许多题目我们都解过,怎样转化呢?加油吧!
潘 康 林思考与探究如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A= ∠B。如果这两艘救生以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?ABOSOS!SOS!猜想与归纳在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?即:若⊿ABC中,∠B=∠C,则AB与AC有什么关系?点击我,瞧瞧去请用数学符号表示出这句话猜想与归纳如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)⊿ABC中,
∵∠B=∠C
∴AB=AC推理形式如下:猜想与归纳已知⊿ABC中,∠ABC=∠ACB,求证:AB=AC证明:作AD⊥BC,垂足为D,在⊿ABD和⊿ACD中,⊿ABD≌ ⊿ACD∴例题分析例2、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
已知:∠CAE是⊿ABC的外角,∠1=∠2,AD//BC,(如图),求证:AB=AC。证明:∵AD//BC∴∠1=∠B∴∠2=∠C又已知∠1=∠2∴∠B=∠CAB=AC(_______________________)(_____________________________)(____________________)两直线平行,内错角相等等角对等边两直线平行,同位角相等例题分析例3、如图,标杆AB高5 m,为了将它固定,需要由它的中点C向地面上与点B 距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4 m,绳子CD和CE要多长?分析:1、CD与CE相等吗?为什么?2、若用作图的方式来解决,取比例尺为多少较好?为什么?3、若要作图,问题即是:已知三角形的CDE是等腰三角形,且底边上的高CB=2.5 m,底边DE长为4 m,能否作出这个三角形?动手操作看看吧!你能行!也请看看我的作法!CD与CE相等,因为AB是线段DE的垂直平分线。取1:100较好,此时1 cm代表了1 m,换算方便。练习1、如图,∠A=360,∠DBC=360,∠C=720,分别计算∠1、 ∠2的度数。答案:提示:∠1= 720,∠2=360由∠A=360,∠C=720得: ∠ABC=720在⊿ABC中∵ ∠DBC=360,∠1= ∠A+ ∠2 =360+360=720∴∠2=360练习2、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?ABCEDC答:重合部分是一个等腰三角形。∵由折叠可知∠ECD=∠EAB,∠C=∠A ,CD=AB,∴⊿EAB≌⊿ECD(AAS)∴EB=ED动画演示练习3、如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD。证明:∵ OA=OB∴∠OAB=∠0BA又∵ AB∥DC∴∠OCD=∠OAB
∠0DC =∠0BA(平行线的性质)∴∠OCD=∠ODC∴OC=OD生活应用上午八时,一条船从海岛A出发,以15海里的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得∠NAC=420,∠NBC=840,求从海岛B到灯塔C的距离。ABCN解:∵ ∠NBC=∠A+∠C(三角形的一个外角等于不相邻的两个内角的和)∴∠C= 840-420=420∴BA=BC(等角对等边)∵ AB=15(10-8)=30∴BC=BA=30(海里)思考拓展1、如图,⊿ABC中,BC=BA,∠A=600,BD是AC边的中线,延长BC到E,使CE=CD,求证:DE=DB提示:∵ BA=BC∴∠BCA=∠A=600(等边对等角)∵ CE=CD∴∠E=∠CDE=300(三角形外角性质)∵ BD是AC边的中线∴∠DBC=300(等腰三角形的性质)∴DE=DB(等角对等边)若DB是AC边上的高,上述结论还成立吗?若DB是AC边上的高,上述结论仍成立思考拓展1、如图,⊿ABC中,∠ABC、∠ACB的平分线交于点O,过点O作DE//BC,分别交AB、AC于点D、E,求证:BD+EC=DE提示:∵ DE//BC∴∠OBC=∠DOB,∠OCB=∠EOC∵ BO、CO分别平分∠ABC、∠ACB∴∠DBO=∠DOB=∠OBC,∠ECO=∠EOC=∠OCB∴BD=DO,CE=OE ∴BD+EC=DO+OE=DE(等角对等边)小结知识本节课你学到了等腰三角形的什么知识?
等角对等边可运用在什么方面?(证明两线段相等)作业课本:
P150 第十二题、第十三题再见著名的数学家,莫斯科大学教授雅洁卡提出:“解题就是把要解的题转化为已经解过的题”。许多题目我们都解过,怎样转化呢?加油吧!
