第二十二章二次函数阶段复习课
文档属性
| 名称 | 第二十二章二次函数阶段复习课 |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-11-02 00:00:00 | ||
图片预览

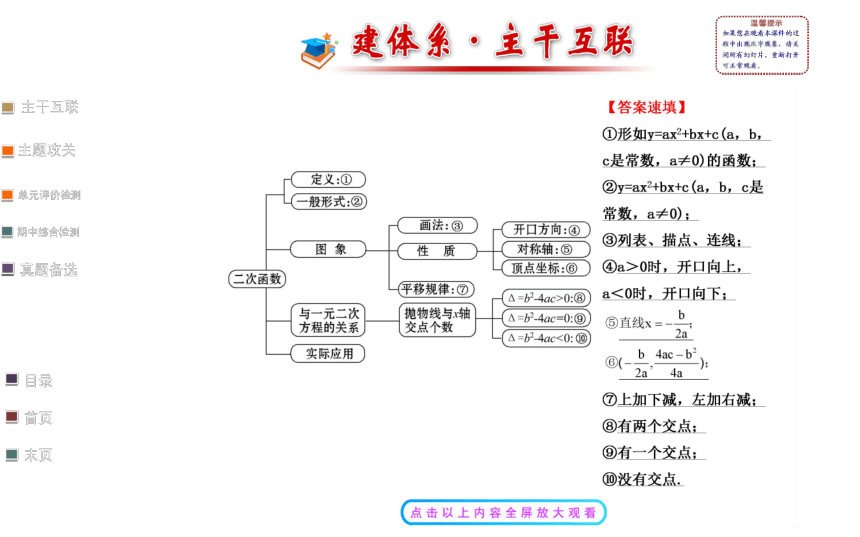










文档简介
课件42张PPT。阶段复习课
第二十二章主题1 二次函数的平移
【主题训练1】(2013·枣庄中考)将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
A.y=3(x+2)2+3 B.y=3(x-2)2+3
C.y=3(x+2)2-3 D.y=3(x-2)2-3【自主解答】选A.由“上加下减”的平移规律可知,将抛物线y=3x2向上平移3个单位所得抛物线的解析式为:y=3x2+3;由“左加右减”的平移规律可知,将抛物线y=3x2+3向左平移2个单位所得抛物线的解析式为:y=3(x+2)2+3.【主题升华】
二次函数平移的两种方法
1.确定顶点坐标平移:根据两抛物线前后顶点坐标的位置确定平移的方向与距离.
2.利用规律平移:y=a(x+h)2+k是由y=ax2经过适当的平移得到的,其平移规律是“h左加右减,k上加下减”.即自变量加减左右移,函数值加减上下移.1.(2013·茂名中考)下列二次函数的图象,不能通过函数y=3x2的图象平移得到的是( )
A.y=3x2+2 B.y=3(x-1)2
C.y=3(x-1)2+2 D.y=2x2
【解析】选D.函数y=3x2的图象平移后,二次项系数仍然是3,不可能变为2,所以D选项中二次函数的图象不能通过函数y=3x2的图象平移得到.2.(2013·衢州中考)抛物线y=x2+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为y=(x-1)2-4,则b,c的值为( )
A.b=2,c=-6 B.b=2,c=0
C.b=-6,c=8 D.b=-6,c=2【解析】选B.平移后的顶点为(1,-4),根据平移前后是相反的
过程可知(1,-4)向左平移2个单位,再向上平移3个单位得到y=x2+bx+c的顶点为(-1,-1),所以原抛物线的解析式y=(x+1)2-1,化成一般形式为y=x2+2x,故b=2,c=0.【知识归纳】二次函数之间的平移关系
1.二次函数y=ax2先向右平移h(h>0)个单位,再向上平移k(k>0)个单位得二次函数y=a(x-h)2+k.
2.二次函数y=a(x-h)2+k先向下平移k(k>0)个单位,再向左平移h(h>0)个单位得二次函数y=ax2.主题2 二次函数的图象及性质
【主题训练2】(2013·十堰中考)如图,二次函数y=ax2+bx+c (a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0),下列结论:①ab<0;②b2>4a;③0-1时,y>0.其中正确结论的个数是( )
A.5个 B.4个 C.3个 D.2个【自主解答】选B.①∵对称轴在y轴右侧,∴- >0,∴ <0,
∴a,b异号,∴ab<0,①正确;②把x=0,y=1代入y=ax2+bx+c得c=1,
所以二次函数为y=ax2+bx+1; 又∵图象与x轴有两个交点,
∴b2-4ac>0,∴b2>4a,②正确;③∵当x=1时,图象在x轴上方,
∴a+b+c>0;把x=-1,y=0代入y=ax2+bx+1,得b=a+1,∵图象的开
口向下,∴a<0,∴a+b+c= a+a+1+1=2a+2<2,∴0确;④∵b=a+1,∴a=b-1,∵00<2b<2,∴0-1时,函数图象有部分在x轴上
方,与x轴有交点,有部分在x轴下方,所以y>0,y=0,y<0都有可能.
所以正确的共有4个,选B.【主题升华】1.(2013·长沙中考)二次函数y=ax2+bx+c的图象如图所示,
则下列关系式错误的是( )
A.a>0
B.c>0
C.b2-4ac>0
D.a+b+c>0【解析】选D.2.(2013·陕西中考)已知两点A(-5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点,若y1>y2 ≥y0,则x0的取值范围是( )
A.x0>-5 B.x0>-1
C.-5y2≥y0,∴抛物线开口向上,且对称轴不可能
在A点的左侧;若对称轴在B点或其右侧,此时满足题意,则有
x0≥3;若对称轴在A,B两点之间,当y1=y2时,有x0=-1,当y1>y2时,
应有x0> ,即3>x0>-1,综上可得x0的取值范围是x0>-1.【变式训练】(2013·河池中考)已知二次函数y=-x2+3x- ,
当自变量x取m时对应的函数值大于0,设自变量x分别取m-3,m+3
时对应的函数值为y1,y2,则( )
A.y1>0,y2>0 B.y1>0,y2<0
C.y1<0,y2>0 D.y1<0,y2<0【解析】选D.方法一:当m=1时,y>0;当m=-2时,y1<0;
当m=4时,y2<0;故选D.
方法二:二次函数y=-x2+3x- 的对称轴是x= ,
当x=0和3时,函数值都是- ,所以当自变量x分别取m-3,m+3时
对应的函数值为y1,y2都是负数.【方法技巧】二次函数比较大小的三种方法
1.代入数值计算函数值比较大小.
2.在对称轴的同侧根据函数的增减性比较大小.
3.在对称轴的异侧根据开口方向和距对称轴距离的远近比较大小.3.(2013·绵阳中考)二次函数y=ax2+bx+c
的图象如图所示,给出下列结论:①2a+b>0;
②b>a>c;③若-1④3|a|+|c|<2|b|.其中正确的结论是
(写出你认为正确的所有结论序号).【解析】对称轴x= >1,所以b>-2a,即2a+b>0,故①正
确;抛物线开口向下,a<0,与y轴交于负半轴,c<0,对称
轴x= >0,∴b>0.根据图象无法确定a与c的大小,故②不
正确;因为-1<m<n<1,∴ <1,而对称轴x= >
1,所以 < ,即m+n< ,故③正确;因为x=1时,
a+b+c>0,而2a+b>0,∴2a+b+a+b+c>0,所以3|a|-2|b|
+|c|=-3a-2b-c=-(3a+2b+c)<0,即3|a|+|c|<2|b|,故
④正确.
答案:①③④主题3 二次函数与方程、不等式
【主题训练3】(2013·贺州中考)已知二
次函数y=ax2+bx+c(a≠0)的图象如图所示,
给出以下结论:①b2>4ac;②abc>0;③2a-b
=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确
的是 .(填入正确结论的序号)【自主解答】∵抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,
∴一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,
∴b2-4ac>0,即b2>4ac,①是正确的.
∵抛物线的开口方向向上,∴a>0;
∵抛物线与y轴的交点在y轴的负半轴,∴c<0;
∵对称轴x= =1>0,∴a与b异号,则b<0.
∴abc>0,②是正确的.∵抛物线的对称轴x= =1,
∴b=-2a,∴2a+b=0,③是错误的.∵当x=-2时,y=4a-2b+c>0,又∵b=-2a,
∴4a-2b+c=4a-2(-2a)+c=8a+c>0,④是错误的.
∵抛物线的对称轴为直线x=1,∴在x=-1与x=3时函数值相等,由函数图象可知x=-1的函数值为负数,∴x=3时的函数值y=9a+3b+c<0,⑤是正确的.
答案:①②⑤【主题升华】
二次函数与方程、不等式的关系
1.二次函数与方程:抛物线y=ax2+bx+c与x轴交点的横坐标满足ax2+bx+c=0.
2.二次函数与不等式:抛物线y=ax2+bx+c在x轴上方部分的横坐标满足ax2+bx+c>0;抛物线y=ax2+bx+c在x轴下方部分的横坐标满足ax2+bx+c<0.1.(2013·昭通中考)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小【解析】选B.∵抛物线开口向下,∴a<0,故A选项错误;∵对称轴x=1,∴另一个根为1+2=3,故B选项正确;∵对称轴x=1,∴当x=1时,y=a+b+c>0,所以C选项错误;当x<1时,y随x的增大而增大,所以D选项错误.2.(2013·宁波中考)如图,二次函数y=ax2
+bx+c的图象开口向上,对称轴为直线x=1,
图象经过(3,0),下列结论中,正确的一项
是( )
A.abc<0 B.2a+b<0
C.a-b+c<0 D.4ac-b2<0【解析】选D.A、根据图象可知,抛物线开口方向向上,则a>0.
抛物线的对称轴x= =1>0,则b<0.抛物线与y轴交于负半轴,
则c<0,所以abc>0.故本选项错误;
B、∵x= =1,∴b=-2a,∴2a+b=0.故本选项错误;
C、∵对称轴为直线x=1,图象经过(3,0),
∴该抛物线与x轴的另一交点的坐标是(-1,0),
∴当x=-1时,y=0,即a-b+c=0.故本选项错误;
D、根据图象可知,该抛物线与x轴有两个不同的交点,则Δ=
b2-4ac>0,则4ac-b2<0.故本选项正确.主题4 二次函数的应用
【主题训练4】(2013·武汉中考)科幻小说《实验室的故事》中,有这样一个情节:科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如表).由这些数据,科学家推测出植物每天高度增长量y是温度x的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由.
(2)温度为多少时,这种植物每天高度增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度x应该在哪个范围内选择?直接写出结果.【自主解答】(1)选择二次函数.设抛物线的解析式为y=ax2+bx+c,
根据题意,得
∴y关于x的函数解析式为y=-x2-2x+49.
不选另外两个函数的理由:点(0,49)不可能在任何反比例函数图象上,所以y不是x的反比例函数;点(-4,41),(-2,49),(2,41)不在同一直线上,所以y不是x的一次函数.(2)由(1)得y=-x2-2x+49,∴y=-(x+1)2+50.
∵a=-1<0,∴当x=-1时y的最大值为50.
即当温度为-1℃时,这种植物每天高度增长量最大.
(3)-6解决二次函数应用题的两步骤
1.建模:根据数量关系列二次函数关系建模或者根据图象的形状建模.
2.应用:利用二次函数的性质解决问题.1.(2013·仙桃中考)2013年5月26日,中国羽毛球队蝉联苏迪曼
杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运
动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛
球行进高度y(m)与水平距离x(m)之间满足关系
则羽毛球飞出的水平距离为 m.【解析】令y=0,得: 解得:x1=5,x2=
-1(不合题意,舍去),所以羽毛球飞出的水平距离为5 m.
答案:52.(2013·鞍山中考)某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x之间的函数关系式.
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?【解析】(1)由题意,可设y=kx+b(k≠0),把(5,30000),(6,20000)代入得
所以y与x之间的关系式为:y=-10000x+80000.
(2)设每月的利润为W,则W=(x-4)(-10000x+80000)
=-10000(x-4)(x-8)=-10000(x2-12x+32)
=-10000[(x-6)2-4]=-10000(x-6)2+40000.
所以当x=6时,W取得最大值,最大值为40000元.
答:当销售价格定为每件6元时,每月的利润最大,每月的最大利润为40000元.
第二十二章主题1 二次函数的平移
【主题训练1】(2013·枣庄中考)将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )
A.y=3(x+2)2+3 B.y=3(x-2)2+3
C.y=3(x+2)2-3 D.y=3(x-2)2-3【自主解答】选A.由“上加下减”的平移规律可知,将抛物线y=3x2向上平移3个单位所得抛物线的解析式为:y=3x2+3;由“左加右减”的平移规律可知,将抛物线y=3x2+3向左平移2个单位所得抛物线的解析式为:y=3(x+2)2+3.【主题升华】
二次函数平移的两种方法
1.确定顶点坐标平移:根据两抛物线前后顶点坐标的位置确定平移的方向与距离.
2.利用规律平移:y=a(x+h)2+k是由y=ax2经过适当的平移得到的,其平移规律是“h左加右减,k上加下减”.即自变量加减左右移,函数值加减上下移.1.(2013·茂名中考)下列二次函数的图象,不能通过函数y=3x2的图象平移得到的是( )
A.y=3x2+2 B.y=3(x-1)2
C.y=3(x-1)2+2 D.y=2x2
【解析】选D.函数y=3x2的图象平移后,二次项系数仍然是3,不可能变为2,所以D选项中二次函数的图象不能通过函数y=3x2的图象平移得到.2.(2013·衢州中考)抛物线y=x2+bx+c的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为y=(x-1)2-4,则b,c的值为( )
A.b=2,c=-6 B.b=2,c=0
C.b=-6,c=8 D.b=-6,c=2【解析】选B.平移后的顶点为(1,-4),根据平移前后是相反的
过程可知(1,-4)向左平移2个单位,再向上平移3个单位得到y=x2+bx+c的顶点为(-1,-1),所以原抛物线的解析式y=(x+1)2-1,化成一般形式为y=x2+2x,故b=2,c=0.【知识归纳】二次函数之间的平移关系
1.二次函数y=ax2先向右平移h(h>0)个单位,再向上平移k(k>0)个单位得二次函数y=a(x-h)2+k.
2.二次函数y=a(x-h)2+k先向下平移k(k>0)个单位,再向左平移h(h>0)个单位得二次函数y=ax2.主题2 二次函数的图象及性质
【主题训练2】(2013·十堰中考)如图,二次函数y=ax2+bx+c (a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0),下列结论:①ab<0;②b2>4a;③0
A.5个 B.4个 C.3个 D.2个【自主解答】选B.①∵对称轴在y轴右侧,∴- >0,∴ <0,
∴a,b异号,∴ab<0,①正确;②把x=0,y=1代入y=ax2+bx+c得c=1,
所以二次函数为y=ax2+bx+1; 又∵图象与x轴有两个交点,
∴b2-4ac>0,∴b2>4a,②正确;③∵当x=1时,图象在x轴上方,
∴a+b+c>0;把x=-1,y=0代入y=ax2+bx+1,得b=a+1,∵图象的开
口向下,∴a<0,∴a+b+c= a+a+1+1=2a+2<2,∴0
方,与x轴有交点,有部分在x轴下方,所以y>0,y=0,y<0都有可能.
所以正确的共有4个,选B.【主题升华】1.(2013·长沙中考)二次函数y=ax2+bx+c的图象如图所示,
则下列关系式错误的是( )
A.a>0
B.c>0
C.b2-4ac>0
D.a+b+c>0【解析】选D.2.(2013·陕西中考)已知两点A(-5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点,若y1>y2 ≥y0,则x0的取值范围是( )
A.x0>-5 B.x0>-1
C.-5
在A点的左侧;若对称轴在B点或其右侧,此时满足题意,则有
x0≥3;若对称轴在A,B两点之间,当y1=y2时,有x0=-1,当y1>y2时,
应有x0> ,即3>x0>-1,综上可得x0的取值范围是x0>-1.【变式训练】(2013·河池中考)已知二次函数y=-x2+3x- ,
当自变量x取m时对应的函数值大于0,设自变量x分别取m-3,m+3
时对应的函数值为y1,y2,则( )
A.y1>0,y2>0 B.y1>0,y2<0
C.y1<0,y2>0 D.y1<0,y2<0【解析】选D.方法一:当m=1时,y>0;当m=-2时,y1<0;
当m=4时,y2<0;故选D.
方法二:二次函数y=-x2+3x- 的对称轴是x= ,
当x=0和3时,函数值都是- ,所以当自变量x分别取m-3,m+3时
对应的函数值为y1,y2都是负数.【方法技巧】二次函数比较大小的三种方法
1.代入数值计算函数值比较大小.
2.在对称轴的同侧根据函数的增减性比较大小.
3.在对称轴的异侧根据开口方向和距对称轴距离的远近比较大小.3.(2013·绵阳中考)二次函数y=ax2+bx+c
的图象如图所示,给出下列结论:①2a+b>0;
②b>a>c;③若-1
(写出你认为正确的所有结论序号).【解析】对称轴x= >1,所以b>-2a,即2a+b>0,故①正
确;抛物线开口向下,a<0,与y轴交于负半轴,c<0,对称
轴x= >0,∴b>0.根据图象无法确定a与c的大小,故②不
正确;因为-1<m<n<1,∴ <1,而对称轴x= >
1,所以 < ,即m+n< ,故③正确;因为x=1时,
a+b+c>0,而2a+b>0,∴2a+b+a+b+c>0,所以3|a|-2|b|
+|c|=-3a-2b-c=-(3a+2b+c)<0,即3|a|+|c|<2|b|,故
④正确.
答案:①③④主题3 二次函数与方程、不等式
【主题训练3】(2013·贺州中考)已知二
次函数y=ax2+bx+c(a≠0)的图象如图所示,
给出以下结论:①b2>4ac;②abc>0;③2a-b
=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确
的是 .(填入正确结论的序号)【自主解答】∵抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,
∴一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,
∴b2-4ac>0,即b2>4ac,①是正确的.
∵抛物线的开口方向向上,∴a>0;
∵抛物线与y轴的交点在y轴的负半轴,∴c<0;
∵对称轴x= =1>0,∴a与b异号,则b<0.
∴abc>0,②是正确的.∵抛物线的对称轴x= =1,
∴b=-2a,∴2a+b=0,③是错误的.∵当x=-2时,y=4a-2b+c>0,又∵b=-2a,
∴4a-2b+c=4a-2(-2a)+c=8a+c>0,④是错误的.
∵抛物线的对称轴为直线x=1,∴在x=-1与x=3时函数值相等,由函数图象可知x=-1的函数值为负数,∴x=3时的函数值y=9a+3b+c<0,⑤是正确的.
答案:①②⑤【主题升华】
二次函数与方程、不等式的关系
1.二次函数与方程:抛物线y=ax2+bx+c与x轴交点的横坐标满足ax2+bx+c=0.
2.二次函数与不等式:抛物线y=ax2+bx+c在x轴上方部分的横坐标满足ax2+bx+c>0;抛物线y=ax2+bx+c在x轴下方部分的横坐标满足ax2+bx+c<0.1.(2013·昭通中考)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小【解析】选B.∵抛物线开口向下,∴a<0,故A选项错误;∵对称轴x=1,∴另一个根为1+2=3,故B选项正确;∵对称轴x=1,∴当x=1时,y=a+b+c>0,所以C选项错误;当x<1时,y随x的增大而增大,所以D选项错误.2.(2013·宁波中考)如图,二次函数y=ax2
+bx+c的图象开口向上,对称轴为直线x=1,
图象经过(3,0),下列结论中,正确的一项
是( )
A.abc<0 B.2a+b<0
C.a-b+c<0 D.4ac-b2<0【解析】选D.A、根据图象可知,抛物线开口方向向上,则a>0.
抛物线的对称轴x= =1>0,则b<0.抛物线与y轴交于负半轴,
则c<0,所以abc>0.故本选项错误;
B、∵x= =1,∴b=-2a,∴2a+b=0.故本选项错误;
C、∵对称轴为直线x=1,图象经过(3,0),
∴该抛物线与x轴的另一交点的坐标是(-1,0),
∴当x=-1时,y=0,即a-b+c=0.故本选项错误;
D、根据图象可知,该抛物线与x轴有两个不同的交点,则Δ=
b2-4ac>0,则4ac-b2<0.故本选项正确.主题4 二次函数的应用
【主题训练4】(2013·武汉中考)科幻小说《实验室的故事》中,有这样一个情节:科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如表).由这些数据,科学家推测出植物每天高度增长量y是温度x的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由.
(2)温度为多少时,这种植物每天高度增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度x应该在哪个范围内选择?直接写出结果.【自主解答】(1)选择二次函数.设抛物线的解析式为y=ax2+bx+c,
根据题意,得
∴y关于x的函数解析式为y=-x2-2x+49.
不选另外两个函数的理由:点(0,49)不可能在任何反比例函数图象上,所以y不是x的反比例函数;点(-4,41),(-2,49),(2,41)不在同一直线上,所以y不是x的一次函数.(2)由(1)得y=-x2-2x+49,∴y=-(x+1)2+50.
∵a=-1<0,∴当x=-1时y的最大值为50.
即当温度为-1℃时,这种植物每天高度增长量最大.
(3)-6
1.建模:根据数量关系列二次函数关系建模或者根据图象的形状建模.
2.应用:利用二次函数的性质解决问题.1.(2013·仙桃中考)2013年5月26日,中国羽毛球队蝉联苏迪曼
杯团体赛冠军,成就了首个五连冠霸业.比赛中羽毛球的某次运
动路线可以看作是一条抛物线(如图).若不考虑外力因素,羽毛
球行进高度y(m)与水平距离x(m)之间满足关系
则羽毛球飞出的水平距离为 m.【解析】令y=0,得: 解得:x1=5,x2=
-1(不合题意,舍去),所以羽毛球飞出的水平距离为5 m.
答案:52.(2013·鞍山中考)某商场购进一批单价为4元的日用品.若按每件5元的价格销售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件,假定每月销售件数y(件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x之间的函数关系式.
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?【解析】(1)由题意,可设y=kx+b(k≠0),把(5,30000),(6,20000)代入得
所以y与x之间的关系式为:y=-10000x+80000.
(2)设每月的利润为W,则W=(x-4)(-10000x+80000)
=-10000(x-4)(x-8)=-10000(x2-12x+32)
=-10000[(x-6)2-4]=-10000(x-6)2+40000.
所以当x=6时,W取得最大值,最大值为40000元.
答:当销售价格定为每件6元时,每月的利润最大,每月的最大利润为40000元.
同课章节目录
