人教版高中数学选择性必修第一册1.2 第二课时 空间向量基本定理的初步应用 课件(共32张PPT)
文档属性
| 名称 | 人教版高中数学选择性必修第一册1.2 第二课时 空间向量基本定理的初步应用 课件(共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
第二课时 空间向量基本定理的初步应用
[学习目标] 应用空间向量基本定理解决简单的空间几何体中的平行、垂直、夹角和距离等问题.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
问题1 用向量解决几何问题的一般步骤是什么?
问题2 用向量求两条异面直线的夹角时,两个向量的夹角与两条异面直线的夹角有何关系?
[预习自测]
1.对空间两个非零向量a,b,“a+b=0”是“a∥b”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析:若a+b=0,则a=-b,故a∥b,即充分性成立.
若a∥b,则有a=λb,且λ≠0,故不一定有a=-b,即必要性不成立.
A
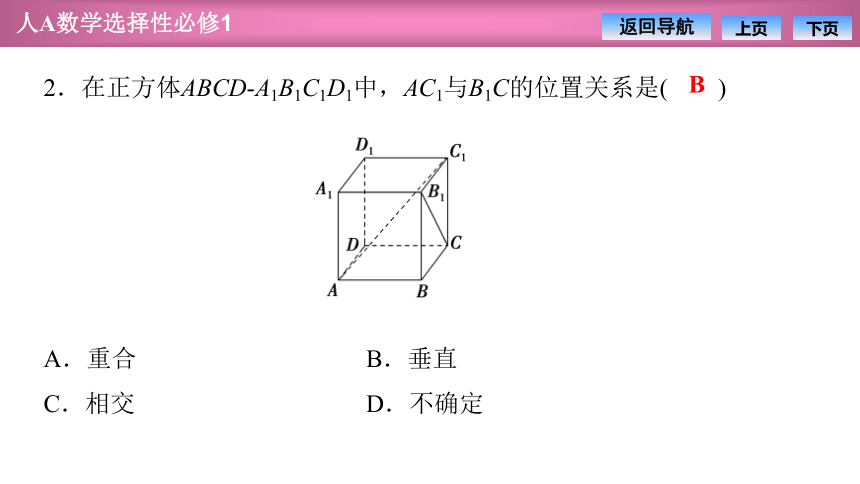
2.在正方体ABCD A1B1C1D1中,AC1与B1C的位置关系是( )
A.重合 B.垂直
C.相交 D.不确定
B
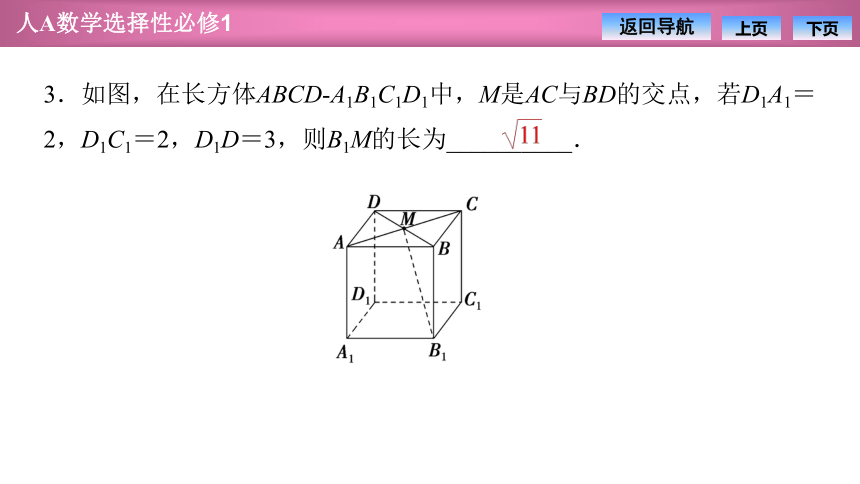
3.如图,在长方体ABCD A1B1C1D1中,M是AC与BD的交点,若D1A1=2,D1C1=2,D1D=3,则B1M的长为__________.
4.已知三棱柱ABC A1B1C1的侧棱垂直于底面,∠BAC=90°,则△ABC1是__________三角形.
直角
应用空间向量基本定理证明平行、垂直
[例1] 如图,在平行六面体ABCD A1B1C1D1中,AB=4,AD=4,AA1=5,∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M,N分别为D1C1,C1B1的中点.求证:(1)MN⊥AC1;(2)MN∥BD.
应用空间向量基本定理证明空间的线线垂直、线线平行的基本思路:
首先根据几何体的特点,选择一个基底,把题目中涉及的两条直线所在的向量用基向量表示.
(1)若证明线线垂直,只需证明两向量数量积为0.
(2)若证明线线平行,只需证明两向量共线.
1.如图,空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC,M,N分别是OA,BC的中点,G是MN的中点,求证:OG⊥BC.
解析:[证明] 连接ON,设∠AOB=∠BOC=∠AOC=θ,
应用空间向量基本定理求夹角、距离
[例2] 如图,在平行六面体ABCD A1B1C1D1中,以顶点A为端点的三条棱长度都为1,且两两夹角为60°.
利用数量积求夹角或其余弦值的步骤
2.如图所示,已知平行六面体ABCD A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,∠A1AB=∠A1AD=120°.
(1)求线段AC1的长;
(2)求证AA1⊥BD;
(3)求异面直线AC1与A1D所成角的余弦值.
1.知识清单:(1)利用空间向量基本定理证明平行、垂直.
(2)利用空间向量基本定理求夹角、距离.
2.方法归纳:数形结合、转化的思想.
课时作业 巩固提升
第二课时 空间向量基本定理的初步应用
[学习目标] 应用空间向量基本定理解决简单的空间几何体中的平行、垂直、夹角和距离等问题.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
问题1 用向量解决几何问题的一般步骤是什么?
问题2 用向量求两条异面直线的夹角时,两个向量的夹角与两条异面直线的夹角有何关系?
[预习自测]
1.对空间两个非零向量a,b,“a+b=0”是“a∥b”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析:若a+b=0,则a=-b,故a∥b,即充分性成立.
若a∥b,则有a=λb,且λ≠0,故不一定有a=-b,即必要性不成立.
A
2.在正方体ABCD A1B1C1D1中,AC1与B1C的位置关系是( )
A.重合 B.垂直
C.相交 D.不确定
B
3.如图,在长方体ABCD A1B1C1D1中,M是AC与BD的交点,若D1A1=2,D1C1=2,D1D=3,则B1M的长为__________.
4.已知三棱柱ABC A1B1C1的侧棱垂直于底面,∠BAC=90°,则△ABC1是__________三角形.
直角
应用空间向量基本定理证明平行、垂直
[例1] 如图,在平行六面体ABCD A1B1C1D1中,AB=4,AD=4,AA1=5,∠DAB=60°,∠BAA1=60°,∠DAA1=60°,M,N分别为D1C1,C1B1的中点.求证:(1)MN⊥AC1;(2)MN∥BD.
应用空间向量基本定理证明空间的线线垂直、线线平行的基本思路:
首先根据几何体的特点,选择一个基底,把题目中涉及的两条直线所在的向量用基向量表示.
(1)若证明线线垂直,只需证明两向量数量积为0.
(2)若证明线线平行,只需证明两向量共线.
1.如图,空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC,M,N分别是OA,BC的中点,G是MN的中点,求证:OG⊥BC.
解析:[证明] 连接ON,设∠AOB=∠BOC=∠AOC=θ,
应用空间向量基本定理求夹角、距离
[例2] 如图,在平行六面体ABCD A1B1C1D1中,以顶点A为端点的三条棱长度都为1,且两两夹角为60°.
利用数量积求夹角或其余弦值的步骤
2.如图所示,已知平行六面体ABCD A1B1C1D1中,底面ABCD是边长为1的正方形,AA1=2,∠A1AB=∠A1AD=120°.
(1)求线段AC1的长;
(2)求证AA1⊥BD;
(3)求异面直线AC1与A1D所成角的余弦值.
1.知识清单:(1)利用空间向量基本定理证明平行、垂直.
(2)利用空间向量基本定理求夹角、距离.
2.方法归纳:数形结合、转化的思想.
课时作业 巩固提升
