人教版七年级数学上册4.1.2 点线面体同步测试(含答案)
文档属性
| 名称 | 人教版七年级数学上册4.1.2 点线面体同步测试(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 121.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 00:00:00 | ||
图片预览


文档简介
人教版七年级数学上册4.1.2 点线面体同步测试(含答案)
一、单选题
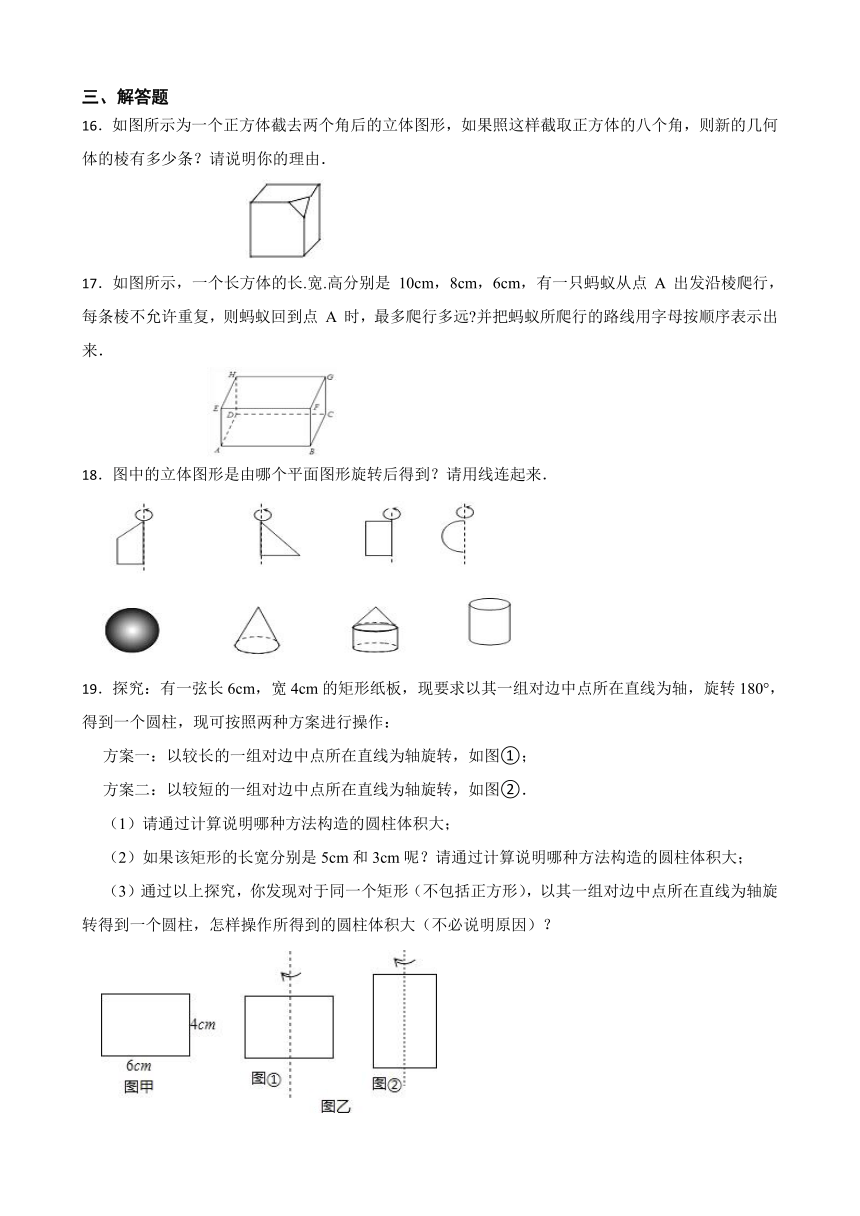
1.下列几何图形与相应语言描述相符的个数有( )
A.1 个 B.2 个 C.3 个 D.4 个
2.如图,用一个平面去截正方体截面形状不可能为下图中的( )
A.B.C.D.
3.观察下图,把左边的图形绕着给定的直线旋转一周后,可能形成的立体图形是( )
A.B.C.D.
4.如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A.B.C.D.
5.用一个平面去截圆柱体,则截面形状不可能是( )
A.正方形 B.三角形 C.长方形 D.圆
6.如图,有一个棱长是 的正方体,从它的一个顶点处挖去一个棱长是 的正方体后,剩下物体的表面积和原来的表面积相比较( )
A.变大了 B.变小了 C.没变 D.无法确定变化
7.用一个平面去截正方体,截面的形状不可能是( )
A.四边形 B.五边形 C.六边形 D.七边形
8.十个棱长为 的正方体摆放成如图的形状,这个图形的表面积是( )
A. B. C. D.
9.用一个平面去截圆柱体,则截面形状不可能是( )
A.梯形 B.正方形 C.长方形 D.圆
10.用一个平面去截下列四个几何体,可以得到三角形截面的几何体有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .
12.一个长方形绕着它的一条边旋转一周,所形成的几何体是 .
13.用个平面去截下列几何体:①球体、②圆锥、③圆柱、④正三枝柱、⑤长方体,得到的截面形状可能是三角形的有 (写出正确的序号).
14.若三棱柱的高为6
cm,底面边长都为5 cm,则三棱柱的侧面展开图的周长为 cm,面积为 cm2.
15.如图,正方体的棱长为a,沿着共一个顶点的三个正方形的对角线裁截掉一个几何体之后,截面△ABC的面积= .
三、解答题
16.如图所示为一个正方体截去两个角后的立体图形,如果照这样截取正方体的八个角,则新的几何体的棱有多少条?请说明你的理由.
17.如图所示,一个长方体的长.宽.高分别是 10cm,8cm,6cm,有一只蚂蚁从点 A 出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点 A 时,最多爬行多远 并把蚂蚁所爬行的路线用字母按顺序表示出来.
18.图中的立体图形是由哪个平面图形旋转后得到?请用线连起来.
19.探究:有一弦长6cm,宽4cm的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:
方案一:以较长的一组对边中点所在直线为轴旋转,如图①;
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)如果该矩形的长宽分别是5cm和3cm呢?请通过计算说明哪种方法构造的圆柱体积大;
(3)通过以上探究,你发现对于同一个矩形(不包括正方形),以其一组对边中点所在直线为轴旋转得到一个圆柱,怎样操作所得到的圆柱体积大(不必说明原因)?
20.长和宽分别是4cm和2cm的长方体分别沿长、宽所在直线旋转一周得到两个几何体,哪个几何体的体积大?为什么?
21.下图是长方体的表面展开图,将它折叠成一个长方体.
(1)哪几个点与点 重合?
(2)若 , , ,求这个长方体的表面积和体积.
22.在一块长为 ,宽为 的长方形铁片的四个角都剪去一个边长为 的小正方形,然后折成一个无盖的盒子,求这个盒子的表面积(用含 、 的代数式表示).
23.有3个棱长分别是3cm,4cm,5cm的正方体组合成如图所示的图形.其露在外面的表面积是多少?(整个立体图形摆放在地上)
24.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4厘米,宽为3厘米的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
答 案
1.C 2.A 3.C 4.B 5.B 6.C 7.D 8.A 9.A 10.B 11.8 12.圆柱体
13.②④⑤ 14.42;90 15.
16.解:∵一个正方体有12条棱,
一个角上裁出3条棱,即8个角共3×8条棱,
∴12+3×8=36条.
故新的几何体的棱有36条
17.解:由于不能重复且最后回到点 A 处,那么经过的棱数便等于经过的顶点数,当走的路线最长时必过所有顶点,则选择合理的路线时尽可能多地经过长为 10CM 的棱即可. ,所以最多爬行 68CM.路线举例: .
18.解:如图.
19.解:(1)方案一:π×32×4=36π(cm3),
方案二:π×22×6=24π(cm3),
∵36π>24π,
∴方案一构造的圆柱的体积大;
(2)方案一:π×()2×3=π(cm3),
方案二:π×()2×5=π(cm3),
∵π>π,
∴方案一构造的圆柱的体积大;
(3)由(1)、(2),得
以较长一组对边中点所在直线为轴旋转得到的圆柱的体积大.
20.【解答】解:分两种情况:
①绕长所在的直线旋转一周得到圆柱体积为:π×22×4=16π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×42×2=32π(cm3).
∵16π<32π,
∴绕宽所在的直线旋转一周得到圆柱体积大.
21.解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
( )若 , , ,求这个长方体的表面积和体积.
解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
(1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
22.解:由题意,得
.
∴这个盒子的表面积为 .
23.解:露在外面的表面积:5×5+4×(3×3+4×4+5×5)=25+4×(9+16+25)=225cm2 .
24.解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.
绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3
一、单选题
1.下列几何图形与相应语言描述相符的个数有( )
A.1 个 B.2 个 C.3 个 D.4 个
2.如图,用一个平面去截正方体截面形状不可能为下图中的( )
A.B.C.D.
3.观察下图,把左边的图形绕着给定的直线旋转一周后,可能形成的立体图形是( )
A.B.C.D.
4.如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是( )
A.B.C.D.
5.用一个平面去截圆柱体,则截面形状不可能是( )
A.正方形 B.三角形 C.长方形 D.圆
6.如图,有一个棱长是 的正方体,从它的一个顶点处挖去一个棱长是 的正方体后,剩下物体的表面积和原来的表面积相比较( )
A.变大了 B.变小了 C.没变 D.无法确定变化
7.用一个平面去截正方体,截面的形状不可能是( )
A.四边形 B.五边形 C.六边形 D.七边形
8.十个棱长为 的正方体摆放成如图的形状,这个图形的表面积是( )
A. B. C. D.
9.用一个平面去截圆柱体,则截面形状不可能是( )
A.梯形 B.正方形 C.长方形 D.圆
10.用一个平面去截下列四个几何体,可以得到三角形截面的几何体有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是 .
12.一个长方形绕着它的一条边旋转一周,所形成的几何体是 .
13.用个平面去截下列几何体:①球体、②圆锥、③圆柱、④正三枝柱、⑤长方体,得到的截面形状可能是三角形的有 (写出正确的序号).
14.若三棱柱的高为6
cm,底面边长都为5 cm,则三棱柱的侧面展开图的周长为 cm,面积为 cm2.
15.如图,正方体的棱长为a,沿着共一个顶点的三个正方形的对角线裁截掉一个几何体之后,截面△ABC的面积= .
三、解答题
16.如图所示为一个正方体截去两个角后的立体图形,如果照这样截取正方体的八个角,则新的几何体的棱有多少条?请说明你的理由.
17.如图所示,一个长方体的长.宽.高分别是 10cm,8cm,6cm,有一只蚂蚁从点 A 出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点 A 时,最多爬行多远 并把蚂蚁所爬行的路线用字母按顺序表示出来.
18.图中的立体图形是由哪个平面图形旋转后得到?请用线连起来.
19.探究:有一弦长6cm,宽4cm的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:
方案一:以较长的一组对边中点所在直线为轴旋转,如图①;
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)如果该矩形的长宽分别是5cm和3cm呢?请通过计算说明哪种方法构造的圆柱体积大;
(3)通过以上探究,你发现对于同一个矩形(不包括正方形),以其一组对边中点所在直线为轴旋转得到一个圆柱,怎样操作所得到的圆柱体积大(不必说明原因)?
20.长和宽分别是4cm和2cm的长方体分别沿长、宽所在直线旋转一周得到两个几何体,哪个几何体的体积大?为什么?
21.下图是长方体的表面展开图,将它折叠成一个长方体.
(1)哪几个点与点 重合?
(2)若 , , ,求这个长方体的表面积和体积.
22.在一块长为 ,宽为 的长方形铁片的四个角都剪去一个边长为 的小正方形,然后折成一个无盖的盒子,求这个盒子的表面积(用含 、 的代数式表示).
23.有3个棱长分别是3cm,4cm,5cm的正方体组合成如图所示的图形.其露在外面的表面积是多少?(整个立体图形摆放在地上)
24.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4厘米,宽为3厘米的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
答 案
1.C 2.A 3.C 4.B 5.B 6.C 7.D 8.A 9.A 10.B 11.8 12.圆柱体
13.②④⑤ 14.42;90 15.
16.解:∵一个正方体有12条棱,
一个角上裁出3条棱,即8个角共3×8条棱,
∴12+3×8=36条.
故新的几何体的棱有36条
17.解:由于不能重复且最后回到点 A 处,那么经过的棱数便等于经过的顶点数,当走的路线最长时必过所有顶点,则选择合理的路线时尽可能多地经过长为 10CM 的棱即可. ,所以最多爬行 68CM.路线举例: .
18.解:如图.
19.解:(1)方案一:π×32×4=36π(cm3),
方案二:π×22×6=24π(cm3),
∵36π>24π,
∴方案一构造的圆柱的体积大;
(2)方案一:π×()2×3=π(cm3),
方案二:π×()2×5=π(cm3),
∵π>π,
∴方案一构造的圆柱的体积大;
(3)由(1)、(2),得
以较长一组对边中点所在直线为轴旋转得到的圆柱的体积大.
20.【解答】解:分两种情况:
①绕长所在的直线旋转一周得到圆柱体积为:π×22×4=16π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×42×2=32π(cm3).
∵16π<32π,
∴绕宽所在的直线旋转一周得到圆柱体积大.
21.解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
( )若 , , ,求这个长方体的表面积和体积.
解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
(1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由 , ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
22.解:由题意,得
.
∴这个盒子的表面积为 .
23.解:露在外面的表面积:5×5+4×(3×3+4×4+5×5)=25+4×(9+16+25)=225cm2 .
24.解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.
绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3
