人教版高中数学选择性必修第一册1.4.1第三课时空间中直线、平面的垂直 课件(共34张PPT)
文档属性
| 名称 | 人教版高中数学选择性必修第一册1.4.1第三课时空间中直线、平面的垂直 课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-20 11:44:54 | ||
图片预览











文档简介
(共34张PPT)
第三课时 空间中直线、平面的垂直
[学习目标]
1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.
2.能用向量方法判定或证明空间直线、平面间的垂直关系.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
问题1 理解并写出空间直线、平面垂直的向量条件?
问题2 用向量解决空间线面垂直问题的一般步骤是什么?
解析:∵l1⊥l2,∴a·b=1×(-2)+2×3-2m=0,
解得m=2.
B
A
3.已知平面α和平面β的法向量分别为a=(1,2,2),b=(x,-2,3),若α⊥β,则x=________.
解析:由题意,得a·b=x-4+6=x+2=0,
解得x=-2.
-2
4.直线l的方向向量为a=(1,0,2),则|a|=__________,若平面α的法向量为n=(-2,0,-4),则直线l与平面α的位置关系__________(填“平行”或“垂直”).
垂直
直线和直线垂直
用向量证明两条直线垂直
a,b是直线l1,l2的方向向量,直线l1与直线l2垂直的充要条件是 .
a⊥b
[例1] 已知空间四边形OABC中,OB=OC,∠AOB=∠AOC=θ,求证:OA⊥BC.
分析:本题考查线线垂直的向量证法.根据向量的数量积运算直接求解即可.
向量法证明两条直线垂直的方法
(1)坐标法:建立空间直角坐标系,写出相关点的坐标,求出两直线方向向量的坐标,然后通过数量积的坐标运算法则证明数量积等于0,从而证明两条直线的方向向量互相垂直.
(2)基向量法:利用空间向量的加法、减法、数乘运算及其运算律,结合图形,将两直线所在的向量用基向量表示,然后根据数量积的运算律证明两直线所在的向量的数量积等于0,从而证明两条直线的方向向量互相垂直.
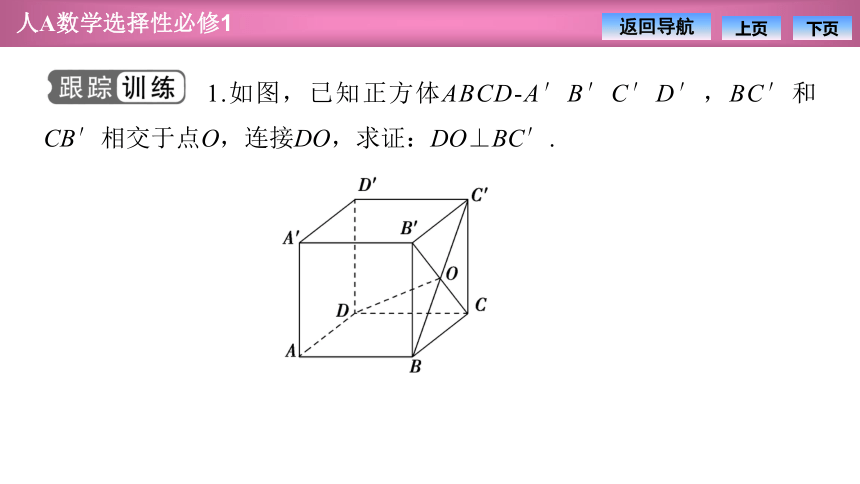
1.如图,已知正方体ABCD A′B′C′D′,BC′和CB′相交于点O,连接DO,求证:DO⊥BC′.
直线和平面垂直
用向量证明直线与平面垂直
a是直线l的方向向量,n是平面α的法向量,直线l与平面α垂直的充要条件是 .
a∥n
[例2] 如图,在长方体ABCD A1B1C1D1中,AB=2,BC=CC1=1,E是CD的中点.求证:B1E⊥平面AED1.
[证明] 建立如图所示空间直角坐标系,
利用空间向量证明线面垂直的方法
(1)基向量法:选取基向量,用基向量表示直线所在的向量,在平面内找出两个不共线的向量,也用基向量表示,然后根据数量积运算律分别证明直线所在向量与两个不共线向量的数量积均为零,从而证明得结论.
(2)坐标法:建立空间直角坐标系,求出直线方向向量的坐标以及平面内两个不共线向量的坐标,然后根据数量积的坐标运算法则证明直线的方向向量与两个不共线向量的数量积均为零,从而证得结论.
(3)法向量法:建立空间直角坐标系,求出直线方向向量的坐标以及平面法向量的坐标,然后说明直线方向向量与平面法向量共线,从而证得结论.
2.如图,在平行六面体ABCD A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
平面和平面垂直
用向量证明两个平面垂直
m,n是平面α,β的法向量,平面α与平面β垂直的充要条件是 .
m⊥n
[例3] 证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:l⊥α,l β,求证:α⊥β.
分析:本题考查面面垂直的判定定理,直线的方向向量,平面的法向量等知识,考查分析推理能力.设直线l的方向向量u,平面β的法向量n,根据向量法可得两平面法向量互相垂直即可证明.
[证明] 取直线l的方向向量u,平面β的法向量n.
因为l⊥α,所以u是平面α的法向量.
因为l β,而n是平面β的法向量,所以u⊥n.
所以α⊥β.
利用空间向量证明面面垂直的方法
(1)转化为线面垂直、线线垂直,然后借助向量共线或垂直进行证明.
(2)通过证明两个平面的法向量垂直证明.
3.如图,已知三棱柱ABC A1B1C1,侧面BCC1B1⊥底面ABC,若三棱柱ABC A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为60°,问在线段A1C1上是否存在一点P,使得平面B1CP⊥平面ACC1A1?若存在,求C1P与PA1的比值;若不存在,说明理由.
解析:取BC的中点O,以O为坐标原点,建立如图空间直角坐标系,
1.知识清单:(1)用向量证明直线和直线垂直.
(2)用向量证明直线和平面垂直.
(3)用向量证明平面和平面垂直.
2.方法归纳:向量法.
3.常见误区:应用空间向量解答探究题有两个思路:(1)观察猜想,找出点或线的位置,再加以证明,得出结论.(2)假设点或参数存在(用相关参数表示),根据线、面的垂直、平行关系求参数,并通过参数值是否符合限定范围来判断是否存在.
课时作业 巩固提升
第三课时 空间中直线、平面的垂直
[学习目标]
1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系.
2.能用向量方法判定或证明空间直线、平面间的垂直关系.
必备知识 自主探究
关键能力 互动探究
课时作业 巩固提升
问题1 理解并写出空间直线、平面垂直的向量条件?
问题2 用向量解决空间线面垂直问题的一般步骤是什么?
解析:∵l1⊥l2,∴a·b=1×(-2)+2×3-2m=0,
解得m=2.
B
A
3.已知平面α和平面β的法向量分别为a=(1,2,2),b=(x,-2,3),若α⊥β,则x=________.
解析:由题意,得a·b=x-4+6=x+2=0,
解得x=-2.
-2
4.直线l的方向向量为a=(1,0,2),则|a|=__________,若平面α的法向量为n=(-2,0,-4),则直线l与平面α的位置关系__________(填“平行”或“垂直”).
垂直
直线和直线垂直
用向量证明两条直线垂直
a,b是直线l1,l2的方向向量,直线l1与直线l2垂直的充要条件是 .
a⊥b
[例1] 已知空间四边形OABC中,OB=OC,∠AOB=∠AOC=θ,求证:OA⊥BC.
分析:本题考查线线垂直的向量证法.根据向量的数量积运算直接求解即可.
向量法证明两条直线垂直的方法
(1)坐标法:建立空间直角坐标系,写出相关点的坐标,求出两直线方向向量的坐标,然后通过数量积的坐标运算法则证明数量积等于0,从而证明两条直线的方向向量互相垂直.
(2)基向量法:利用空间向量的加法、减法、数乘运算及其运算律,结合图形,将两直线所在的向量用基向量表示,然后根据数量积的运算律证明两直线所在的向量的数量积等于0,从而证明两条直线的方向向量互相垂直.
1.如图,已知正方体ABCD A′B′C′D′,BC′和CB′相交于点O,连接DO,求证:DO⊥BC′.
直线和平面垂直
用向量证明直线与平面垂直
a是直线l的方向向量,n是平面α的法向量,直线l与平面α垂直的充要条件是 .
a∥n
[例2] 如图,在长方体ABCD A1B1C1D1中,AB=2,BC=CC1=1,E是CD的中点.求证:B1E⊥平面AED1.
[证明] 建立如图所示空间直角坐标系,
利用空间向量证明线面垂直的方法
(1)基向量法:选取基向量,用基向量表示直线所在的向量,在平面内找出两个不共线的向量,也用基向量表示,然后根据数量积运算律分别证明直线所在向量与两个不共线向量的数量积均为零,从而证明得结论.
(2)坐标法:建立空间直角坐标系,求出直线方向向量的坐标以及平面内两个不共线向量的坐标,然后根据数量积的坐标运算法则证明直线的方向向量与两个不共线向量的数量积均为零,从而证得结论.
(3)法向量法:建立空间直角坐标系,求出直线方向向量的坐标以及平面法向量的坐标,然后说明直线方向向量与平面法向量共线,从而证得结论.
2.如图,在平行六面体ABCD A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
平面和平面垂直
用向量证明两个平面垂直
m,n是平面α,β的法向量,平面α与平面β垂直的充要条件是 .
m⊥n
[例3] 证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
已知:l⊥α,l β,求证:α⊥β.
分析:本题考查面面垂直的判定定理,直线的方向向量,平面的法向量等知识,考查分析推理能力.设直线l的方向向量u,平面β的法向量n,根据向量法可得两平面法向量互相垂直即可证明.
[证明] 取直线l的方向向量u,平面β的法向量n.
因为l⊥α,所以u是平面α的法向量.
因为l β,而n是平面β的法向量,所以u⊥n.
所以α⊥β.
利用空间向量证明面面垂直的方法
(1)转化为线面垂直、线线垂直,然后借助向量共线或垂直进行证明.
(2)通过证明两个平面的法向量垂直证明.
3.如图,已知三棱柱ABC A1B1C1,侧面BCC1B1⊥底面ABC,若三棱柱ABC A1B1C1的各棱长均为2,侧棱BB1与底面ABC所成的角为60°,问在线段A1C1上是否存在一点P,使得平面B1CP⊥平面ACC1A1?若存在,求C1P与PA1的比值;若不存在,说明理由.
解析:取BC的中点O,以O为坐标原点,建立如图空间直角坐标系,
1.知识清单:(1)用向量证明直线和直线垂直.
(2)用向量证明直线和平面垂直.
(3)用向量证明平面和平面垂直.
2.方法归纳:向量法.
3.常见误区:应用空间向量解答探究题有两个思路:(1)观察猜想,找出点或线的位置,再加以证明,得出结论.(2)假设点或参数存在(用相关参数表示),根据线、面的垂直、平行关系求参数,并通过参数值是否符合限定范围来判断是否存在.
课时作业 巩固提升
